uk SHA-2

SHA-2 (англ. Secure Hash Algorithm Version 2 — безпечний алгоритм хешування, версія 2) — збірна назва односторонніх геш-функцій SHA-224, SHA-256, SHA-384 і SHA-512. Геш-функції призначені для створення «відбитків» або «дайджестів» повідомлень довільної бітової довжини. Застосовуються в різних додатках або компонентах, пов'язаних із захистом інформації.

Історія

Геш-функції SHA-2 розроблені Агентством національної безпеки США і опубліковані Національним інститутом стандартів і технології США у федеральному стандарті обробки інформації FIPS PUB 180-2 в серпні 2002 року.^[1] У цей стандарт також увійшла геш-функція SHA-1, розроблена в 1995 році. У лютому 2004 року до FIPS PUB 180-2 була додана SHA-224^[2].

У жовтні 2008 року вийшла нова редакція стандарту — FIPS PUB 180-3.^[3]

В липні 2006 року з'явився стандарт RFC 4634 «Безпечні геш-алгоритми США (SHA і HMAC-SHA)», що описує SHA-1 і сімейство SHA −2.

Агентство національної безпеки від імені держави випустило патент на SHA-2^[4] під ліцензією Royalty Free.^[5]

Алгоритм

Загальний опис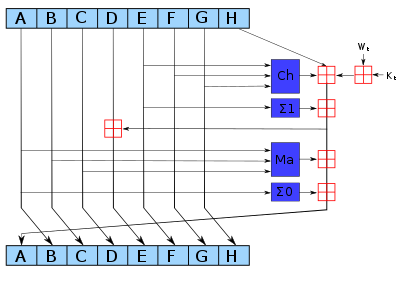

Геш-функції сімейства SHA-2 побудовані на основі структури Меркла-Демґарда.

Початкове повідомлення після доповнення розбивається на блоки, кожен блок — на 16 слів. Алгоритм пропускає кожен блок повідомлення через цикл з 64-ма чи 80-ма ітераціями (раундами). На кожній ітерації 2 слова перетворюються, функцію перетворення задають інші слова. Результати обробки кожного блоку складаються, сума є значенням геш-функції.

Алгоритм використовує такі бітові операції:

ǁ — Конкатенація,
+ — Додавання,
And — Побітове «І»,
Or — Побітове «АБО»,
Xor — Виключне «АБО»,
Shr (Shift Right) — Логічний зсув вправо,
Rotr (Rotate Right) — Циклічний зсув вправо.

У наступній таблиці показані деякі технічні характеристики різних варіантів SHA-2. «Внутрішній стан» означає проміжну геш-суму після обробки чергового блоку даних:

Геш-функція	Довжина дайджесту повідомлення (біт)	Довжина внутрішнього стану (біт)	Довжина блоку (біт)	Максимальна довжина повідомлення (біт)	Довжина слова (біт)	Кількість ітерацій в циклі
SHA-256/224	256/224	256	512	2 ⁶⁴ — 1	32	64
SHA-512/384	512/384	512	1024	2 ¹²⁸ — 1	64	80

Приклади

Нижче наведені приклади гешів SHA-2. Для всіх повідомлень мається на увазі використання кодування ASCII.

SHA-224 ("The quick brown fox jumps over the lazy dog") 
= 730E109B D7A8A32B 1CB9D9A0 9AA2325D 2430587D DBC0C38B AD911525

SHA-256 ("The quick brown fox jumps over the lazy dog")  
= D7A8FBB3 07D78094 69CA9ABC B0082E4F 8D5651E4 6D3CDB76 2D02D0BF 37C9E592

SHA-384 ("The quick brown fox jumps over the lazy dog")   
= CA737F10 14A48F4C 0B6DD43C B177B0AF D9E51693 67544C49 4011E331 
  7DBF9A50 9CB1E5DC 1E85A941 BBEE3D7F 2AFBC9B1

SHA-512 ("The quick brown fox jumps over the lazy dog")  
= 07E547D9 586F6A73 F73FBAC0 435ED769 51218FB7 D0C8D788 A309D785 
  436BBB64 2E93A252 A954F239 12547D1E 8A3B5ED6 E1BFD709 7821233F 
  A0538F3D B854FEE6

Найменша зміна повідомлення в переважній більшості випадків призводить до зовсім іншого гешу внаслідок лавинного ефекту. Наприклад, при зміні dog на cog вийде:

SHA-256 ("The quick brown fox jumps over the lazy cog") 
= E4C4D8F3 BF76B692 DE791A17 3E053211 50F7A345 B46484FE 427F6ACC 7ECC81BE

Криптоаналіз

В 2003 році Гілберт і Хандшух досліджували SHA-2, але не знайшли будь-яких вразливостей^[6]. Проте в березні 2008 року індійські дослідники Сомітра Кумар Санада і Палаш Саркар опублікували знайдені ними колізії для 22 ітерацій SHA-256 і SHA-512^[7]. У вересні того ж року вони представили метод конструювання колізій для усічених варіантів SHA-2 (21 ітерація)^[8].

Криптоаналіз геш-функції досліджує стійкість алгоритму, щонайменше, до таких видів атак:

Знаходження колізій, тобто різних повідомлень з однаковим гешем.
Знаходження прообразу, тобто невідомого повідомлення за його гешем.

Від стійкості геш-функції до знаходження колізій залежить безпека електронного цифрового підпису з використанням цього геш-алгоритму. Від стійкості до знаходження прообразу залежить безпека зберігання гешів паролів для аутентифікації.

Зважаючи на алгоритмічну схожість SHA-2 зі SHA-1 і наявність в останньої потенційних вразливостей шукаються кращі альтернативи^[9]^[10]. Новий стандарт називатиметься SHA-3, його визначать на конкурсі, який проводитиме Національний інститут стандартів і технологій в 2008—2012 роках^[11].

Застосування і сертифікація

Див також Застосування гешування

SHA-224, SHA-256, SHA-384 і SHA-512 допускаються законом США до використання в деяких урядових програмах, включаючи використання в рамках інших криптографічних алгоритмів та протоколів, для захисту інформації, яка не має грифа секретності. Стандарт також допускає використання SHA-2 приватними та комерційними організаціями^[12].

Геш-функції SHA-2 використовуються для перевірки цілісності даних і в різних криптографічних схемах. На 2008 рік сімейство геш-функцій SHA-2 не має такого широкого розповсюдження, як MD5 і SHA-1^[13], незважаючи на виявлені в останніх недоліки.

Як показали дослідження^[14], алгоритми SHA-2 працюють удвічі-втричі повільніше від інших популярних геш-алгоритмів MD5, SHA-1, Tiger та RIPEMD-160.

Примітки

↑ http://csrc.nist.gov/publications/fips/fips180-2/fips180-2.pdf [Архівовано 2012-04-26 у Wayback Machine.] [[https://web.archive.org/web/20220122042946/https://docs.google.com/viewer?url=http%3A%2F%2Fcsrc.nist.gov%2Fpublications%2Ffips%2Ffips180-2%2Ffips180-2.pdf&embedded=true&chrome=false&dov=1 Архівовано 22 січня 2022 у Wayback Machine.] посилання=] FIPS PUB 180-2
↑ http://csrc.nist.gov/publications/fips/fips180-2/fips180-2withchangenotice.pdf [Архівовано 2012-03-12 у Wayback Machine.] [[https://web.archive.org/web/20220120172104/https://docs.google.com/viewer?url=http%3A%2F%2Fcsrc.nist.gov%2Fpublications%2Ffips%2Ffips180-2%2Ffips180-2withchangenotice.pdf&embedded=true&chrome=false&dov=1 Архівовано 20 січня 2022 у Wayback Machine.] посилання=]
↑ http://csrc.nist.gov/publications/fips/fips180-3/fips180-3_final.pdf [Архівовано 2012-03-12 у Wayback Machine.] [[https://web.archive.org/web/20220123063739/https://docs.google.com/viewer?url=http%3A%2F%2Fcsrc.nist.gov%2Fpublications%2Ffips%2Ffips180-3%2Ffips180-3_final.pdf&embedded=true&chrome=false&dov=1 Архівовано 23 січня 2022 у Wayback Machine.] посилання=]
↑ U.S. Patent 6,829,355
↑ Licensing Declaration for US patent 6829355. Архів оригіналу за 16 червня 2016. Процитовано 17 лютого 2008. (англ.)
↑ Архівована копія. Архів оригіналу за 18 жовтня 2011. Процитовано 18 червня 2012.{{cite web}}: Обслуговування CS1: Сторінки з текстом «archived copy» як значення параметру title (посилання)
↑ Somitra Kumar Sanadhya, Palash Sarkar. 22-Step Collisions for SHA-2 [Архівовано 30 березня 2010 у Wayback Machine.] (англ.)
↑ Somitra Kumar Sanadhya, Palash Sarkar. Deterministic Constructions of 21-Step Collisions for the SHA-2 Hash Family (англ.)
↑ / nist_hash_works_4.html Schneier on Security: NIST Hash Workshop Liveblogging (5) [Архівовано 25 квітня 2022 у Wayback Machine.] (англ.)
↑ --/features/75686/2 Hash cracked — heise Security (англ.)
↑ Tentative Timeline of the Development of New Hash Functions [Архівовано 4 червня 2009 у Wayback Machine.] (англ.)
↑ FIPS 180-2: Secure Hash Standard (SHS): 6. Applicability] (англ.)
↑ SHA-1, SHA-256 в результатах пошукової системи Google
↑ Speed Comparison of Popular Crypto Algorithms [1] [Архівовано 15 жовтня 2008 у Wayback Machine.] (англ.)

Література

Лапоніна О.Р. Архівована копія. Архівовано з джерела 24 січня 2012
Книга: Фергюсон Н., Шнайер Б.: Практична криптографія

Див. також

Посилання

Стандарти

Secure Hash Standard (SHS) (FIPS PUB 180-4)
SHA-3 Standard: Permutation-Based Hash and Extendable-Output Functions [Архівовано 27 січня 2018 у Wayback Machine.]
RFC 3874 A 224-bit One-way Hash Function: SHA-224
RFC 4634 US Secure Hash Algorithms (SHA and HMAC-SHA)

Криптоаналіз

Останні досягнення в криптоаналіз SHA-256/224 [Архівовано 26 січня 2012 у Wayback Machine.] (англ.)
Аналіз усіченого варіанту SHA-256^{[недоступне посилання з лютого 2019]} (англ.)
Колізії усіченого варіанту SHA-256 (англ.)
Нелінійні атаки на усічені варіанти геш-функцій SHA-2 (англ.)
Детерміноване конструювання колізій для сімейства гешей SHA-2 з 21 ітерацій (англ.)

Реалізації

The OpenSSL Project [Архівовано 24 квітня 2015 у Wayback Machine.] — широко використовувана бібліотека OpenSSL crypto включає вільні реалізації SHA-224, SHA-256, SHA-384 і SHA-512.
Crypto++ Library [Архівовано 24 лютого 2021 у Wayback Machine.] — вільна реалізація криптографічних алгоритмів на C++
Bouncy Castle Library — вільна бібліотека Java і C # класів, яка включає реалізації SHA-224, SHA-256, SHA-384 і SHA-512, а також інших геш-алгоритмів Whirlpool, Tiger, RIPEMD, ГОСТ Р 34.11-94, MD2, MD4 і MD5
jsSHA [Архівовано 10 січня 2018 у Wayback Machine.] — Онлайн калькулятор та вільна бібліотека Javascript, що включає повне сімейство геш-функцій SHA2, SHA3.
Febooti fileTweak Hash & CRC [Архівовано 3 липня 2012 у Wayback Machine.] — програма для обчислення різних (MD5, SHA-1, SHA-2 та ін) гешів файлів
ReHash [Архівовано 7 січня 2018 у Wayback Machine.] — консольна утиліта обчислення SHA1, SHA-256, SHA-384 і SHA-512.