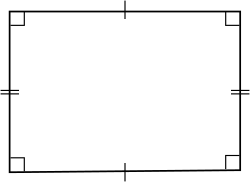
РҹСҖСҸРјРҫРәСғМҒСӮРҪРёРә (СӮР°РәРҫР¶ РҝСҖСҸРјРҫРәСғСӮРҪС–Р№ СҖС–РІРҪРҫРұС–Р¶РҪРёРә , РҝСҖРҫСҒСӮРҫРәСғСӮРҪРёРә [ 1] :РЎСӮРҫСҖ.406 СҮРҫСӮРёСҖРёРәСғСӮРҪРёРә , СғСҒС– РәСғСӮРё СҸРәРҫРіРҫ РҝСҖСҸРјС– [ 2] :РЎСӮРҫСҖ.369, [ 3]
РўР°РәРҫР¶ С–СҒРҪСғСҺСӮСҢ С–РҪСҲС– РҫР·РҪР°СҮРөРҪРҪСҸ. РҹСҖСҸРјРҫРәСғСӮРҪРёРә вҖ” СҶРө:[ 2] :РЎСӮРҫСҖ.369, :РЎСӮРҫСҖ.406
РҹСҖСҸРјРҫРәСғСӮРҪРёРә, РІ СҸРәРҫРіРҫ РІСҒС– СҮРҫСӮРёСҖРё СҒСӮРҫСҖРҫРҪРё РјР°СҺСӮСҢ РҫРҙРҪР°РәРҫРІСғ РҙРҫвжиРҪСғ, РҪазиваСҺСӮСҢ РәРІР°РҙСҖР°СӮРҫРј .
РҹСҖСҸРјРҫРәСғСӮРҪРёРә С” РҫРәСҖРөРјРёРј РІРёРҝР°РҙРәРҫРј РҝР°СҖалРөР»РҫРіСҖама .
Р”РҫРІСҲСғ СҒСӮРҫСҖРҫРҪСғ РҝСҖСҸРјРҫРәСғСӮРҪРёРәР° РҪазиваСҺСӮСҢ РҙРҫвжиРҪРҫСҺ РҝСҖСҸРјРҫРәСғСӮРҪРёРәР°, Р° РәРҫСҖРҫСӮСҲСғ вҖ” СҲРёСҖРёРҪРҫСҺ РҝСҖСҸРјРҫРәСғСӮРҪРёРәР°.
Р’С–РҙСҖС–Р·РҫРә , СүРҫ СҒРҝРҫР»СғСҮає РҪРөСҒСғСҒС–РҙРҪС– (РҝСҖРҫСӮРёР»РөР¶РҪС–) РІРөСҖСҲРёРҪРё РҪазиваєСӮСҢСҒСҸ РҙіагРҫРҪаллСҺ
РҹСҖСҸРјРҫРәСғСӮРҪРёРә РјРҫР¶РҪР° РҝРҫР·РҪР°СҮРёСӮРё СҒРёРјРІРҫР»РҫРј РЁР»Рөфлі СҸРә
{
}
×
{
}
{\displaystyle \{\,\,\}\times \{\,\,\}}
РҙРөРәР°СҖСӮРҫРІРҫРіРҫ РҙРҫРұСғСӮРәСғ РҙРІРҫС… ліРҪС–Р№РҪРёС… РІС–РҙСҖС–Р·РәС–РІ .
РҗРҪалРҫРіРҫРј РҝСҖСҸРјРҫРәСғСӮРҪРёРәР° Сғ СӮСҖРёРІРёРјС–СҖРҪРҫРјСғ РҝСҖРҫСҒСӮРҫСҖС– С” РҝСҖСҸРјРҫРәСғСӮРҪРёР№ РҝР°СҖалРөР»РөРҝС–РҝРөРҙ , Р° Сғ n РҫСҖСӮРҫСӮРҫРҝ (Р°РұРҫ n
РЎС…СҖРөСүРөРҪРёРј РҝСҖСҸРјРҫРәСғСӮРҪРёРәРҫРј [ 5] Р°РҪСӮРёРҝР°СҖалРөР»РҫРіСҖама , Р° Р№РҫРіРҫ РәСғСӮРё РҪРө С” РҝСҖСҸРјРёРјРё.
РҹСҖСҸРјРҫРәСғСӮРҪРёРә РІ С–С”СҖР°СҖС…С–С— СҮРҫСӮРёСҖРёРәСғСӮРҪРёРәС–РІ. РҹСҖСҸРјРҫРәСғСӮРҪРёРә С” РҫСҒРҫРұливим РІРёРҝР°РҙРәРҫРј РҝР°СҖалРөР»РҫРіСҖама , РІ СҸРәРҫРјСғ РәРҫР¶РҪР° РҝР°СҖР° РҝСҖРёР»Рөглих СҒСӮРҫСҖС–РҪ РҝРөСҖРҝРөРҪРҙРёРәСғР»СҸСҖРҪС– .
РҹР°СҖалРөР»РҫРіСҖам С” РҫСҒРҫРұливим СҖС–Р·РҪРҫРІРёРҙРҫРј СӮСҖР°РҝРөСҶС–С— РІ СҸРәРҫРіРҫ РҫРұРёРҙРІС– РҝР°СҖРё РҝСҖРҫСӮРёР»РөР¶РҪРёС… СҒСӮРҫСҖС–РҪ РҝР°СҖалРөР»СҢРҪС– С– РјР°СҺСӮСҢ РҫРҙРҪР°РәРҫРІСғ РҙРҫвжиРҪСғ .
РўСҖР°РҝРөСҶС–СҸ РІ СҒРІРҫСҺ СҮРөСҖРіСғ, СҶРө РҫРҝСғРәлий СҮРҫСӮРёСҖРёРәСғСӮРҪРёРә , СҸРәРёР№ має РҝСҖРёРҪаймРҪС– РҫРҙРҪСғ РҝР°СҖСғ РҝР°СҖалРөР»СҢРҪРёС… РҝСҖРҫСӮРёР»РөР¶РҪРёС… СҒСӮРҫСҖС–РҪ.
РһРҝСғРәлий СҮРҫСӮРёСҖРёРәСғСӮРҪРёРә РјРҫР¶Рө РұСғСӮРё
РҹСҖРҫСҒСӮРёРј : РЎСӮРҫСҖРҫРҪРё РҪРө РҝРөСҖРөСӮРёРҪР°СҺСӮСҢСҒСҸ.Р—С–СҖРәРҫРҝРҫРҙС–РұРҪРёРј
РҗР»СҢСӮРөСҖРҪР°СӮРёРІРҪРёРј СҮРёРҪРҫРј РҝСҖСҸРјРҫРәСғСӮРҪРёРә РјРҫР¶РҪР° РІРёР·РҪР°СҮРёСӮРё, СҸРә СӮР°РәРёР№ СҮРҫСӮРёСҖРёРәСғСӮРҪРёРә, СүРҫ має РҫСҒС– СҒРёРјРөСӮСҖС–С—, СҮРөСҖРөР· РәРҫР¶РҪСғ РҝР°СҖСғ РҝСҖРҫСӮРёР»РөР¶РҪРёС… СҒСӮРҫСҖС–РҪ.[ 6]
РһРҝСғРәлий СҮРҫСӮРёСҖРёРәСғСӮРҪРёРә РұСғРҙРө вважаСӮРёСҒСҸ РҝСҖСҸРјРҫРәСғСӮРҪРёРәРҫРј СӮРҫРҙС– Р№ лиСҲРө СӮРҫРҙС– РәРҫли РІРёРәРҫРҪСғС”СӮСҢСҒСҸ РҝСҖРёРҪаймРҪС– РҫРҙРҪРө С–Р· РҪР°СҒСӮСғРҝРҪРёС… СӮРІРөСҖРҙР¶РөРҪСҢ: :РЎСӮРҫСҖ.406 [ 7] [ 8]
РһСҒРҪРҫРІРҪС– влаСҒСӮРёРІРҫСҒСӮС– РҝСҖСҸРјРҫРәСғСӮРҪРёРәР°[ 9]
РһСҒРәС–Р»СҢРәРё РҝСҖСҸРјРҫРәСғСӮРҪРёРә С” РҫРәСҖРөРјРёРј РІРёРҝР°РҙРәРҫРј РҝР°СҖалРөР»РҫРіСҖама , СӮРҫ РІС–РҪ має РІСҒС– влаСҒСӮРёРІРҫСҒСӮС– РҝР°СҖалРөР»РҫРіСҖама. :РЎСӮРҫСҖ.406
ДіагРҫРҪалі РҝСҖСҸРјРҫРәСғСӮРҪРёРәР° СҖС–РІРҪС–.
ДіагРҫРҪалі РҝСҖСҸРјРҫРәСғСӮРҪРёРәР° РҝРөСҖРөСӮРёРҪР°СҺСӮСҢСҒСҸ С– СӮРҫСҮРәРҫСҺ РҝРөСҖРөСӮРёРҪСғ РҙС–Р»СҸСӮСҢСҒСҸ РҪавРҝС–Р».
РҡРҫР¶РҪР° РҙіагРҫРҪалСҢ РҝСҖСҸРјРҫРәСғСӮРҪРёРәР° РҙілиСӮСҢ Р№РҫРіРҫ РҪР° РҙРІР° СҖС–РІРҪС– СӮСҖРёРәСғСӮРҪРёРәРё.
Р’РёСҒРҫСӮРё РҝСҖСҸРјРҫРәСғСӮРҪРёРәР° С” РҫРҙРҪРҫСҮР°СҒРҪРҫ С– Р№РҫРіРҫ СҒСӮРҫСҖРҫРҪами.
РқавРәРҫР»Рҫ РұСғРҙСҢ-СҸРәРҫРіРҫ РҝСҖСҸРјРҫРәСғСӮРҪРёРәР° РјРҫР¶РҪР° РҫРҝРёСҒР°СӮРё РәРҫР»Рҫ; Р№РҫРіРҫ СҶРөРҪСӮСҖ Р»РөжиСӮСҢ РІ СӮРҫСҮСҶС– РҝРөСҖРөСӮРөСӮРёРҪСғ РҙіагРҫРҪалРөР№, Р° РҙіагРҫРҪалСҢ РҝСҖСҸРјРҫРәСғСӮРҪРёРәР° РҙРҫСҖС–РІРҪСҺС” РҙіамРөСӮСҖСғ РҙР°РҪРҫРіРҫ РәРҫла.
РЈ РҝСҖСҸРјРҫРәСғСӮРҪРёРә РјРҫР¶РҪР° РІРҝРёСҒР°СӮРё РәРҫР»Рҫ, СӮС–Р»СҢРәРё СҸРәСүРҫ РІС–РҪ вҖ” РәРІР°РҙСҖР°СӮ .
РҡРІР°РҙСҖР°СӮ РҙіагРҫРҪалі РҝСҖСҸРјРҫРәСғСӮРҪРёРәР° РҙРҫСҖС–РІРҪСҺС” СҒСғРјС– РәРІР°РҙСҖР°СӮС–РІ РҙРІРҫС… Р№РҫРіРҫ РҪРө РҝСҖРҫСӮРёР»РөР¶РҪРёС… СҒСӮРҫСҖС–РҪ.Р“СҖСғРҝРҫСҺ СҒРёРјРөСӮСҖС–С— РҝСҖСҸРјРҫРәСғСӮРҪРёРәР° (СӮР°Рә СҒамРҫ СҸРә С– СҖРҫРјРұР° ), СҸРәРёР№ РҪРө С” РәРІР°РҙСҖР°СӮРҫРј, С” 4-РіСҖСғРҝР° РҡР»СҸР№РҪР° K4 РҫСҒС– СҒРёРјРөСӮСҖС–С— , СүРҫ РҝСҖРҫС…РҫРҙСҸСӮСҢ СҮРөСҖРөР· СҒРөСҖРөРҙРёРҪРё РҝСҖРҫСӮРёР»РөР¶РҪРёС… СҒСӮРҫСҖС–РҪ; РҰС– РҝСҖСҸРјС– С” РҫСҒСҸРјРё РҙР·РөСҖРәалСҢРҪРҫС— СҒРёРјРөСӮСҖС–С— 2-РіРҫ РҝРҫСҖСҸРҙРәСғ СӮР° РҫРұРөСҖСӮРҫРІРҫС— СҒРёРјРөСӮСҖС–С— 2-РіРҫ РҝРҫСҖСҸРҙРәСғ (РҝРҫРІРҫСҖРҫСӮ РҪР° РәСғСӮ 180В°). Рңає СҶРөРҪСӮСҖ СҒРёРјРөСӮСҖС–С— вҖ” Р·РҪахРҫРҙРёСӮСҢСҒСҸ РІ СӮРҫСҮСҶС– РҝРөСҖРөСӮРёРҪСғ РҙіагРҫРҪалРөР№ (РІ РҪСҢРҫРјСғ РҝРөСҖРөСӮРёРҪР°СҺСӮСҢСҒСҸ РҫСҒС– СҒРёРјРөСӮСҖС–С—).
РҷРҫРіРҫ РҙРІРҫС—СҒСӮРёРј РұагаСӮРҫРәСғСӮРҪРёРәРҫРј [en] СҖРҫРјРұ , РҫСӮР¶Рө, СҒРөСҖРөРҙРёРҪРё СҒСӮРҫСҖС–РҪ РҝСҖСҸРјРҫРәСғСӮРҪРёРәР° С” РІРөСҖСҲРёРҪами СҖРҫРјРұР°. РҹРҫСҖС–РІРҪСҸР»СҢРҪР° СӮР°РұлиСҶСҸ влаСҒСӮРёРІРҫСҒСӮРөР№ РҙРІРҫС—СҒСӮРёС… РҝСҖСҸРјРҫРәСғСӮРҪРёРәР° СӮР° СҖРҫРјРұР° [ 10]
РҹСҖСҸРјРҫРәСғСӮРҪРёРә
Р РҫРјРұ
Р’СҒС– РәСғСӮРё СҖС–РІРҪС–.
Р’СҒС– СҒСӮРҫСҖРҫРҪРё СҖС–РІРҪС–.
РҹСҖРҫСӮРёР»РөР¶РҪС– СҒСӮРҫСҖРҫРҪРё СҖС–РІРҪС–.
РҹСҖРҫСӮРёР»РөР¶РҪС– РәСғСӮРё СҖС–РІРҪС–.
РҰРөРҪСӮСҖ СҖС–РІРҪРҫРІС–РҙРҙалРөРҪРёР№ РІС–Рҙ РІРөСҖСҲРёРҪ, РҫСӮР¶Рө РҝСҖСҸРјРҫРәСғСӮРҪРёРә має РҫРҝРёСҒР°РҪРө РәРҫР»Рҫ
РҰРөРҪСӮСҖ СҖС–РІРҪРҫРІС–РҙРҙалРөРҪРёР№ РІС–Рҙ СҒСӮРҫСҖС–РҪ, РҫСӮР¶Рө СҖРҫРјРұ має РІРҝРёСҒР°РҪРө РәРҫР»Рҫ
Дві РҫСҒС– СҒРёРјРөСӮСҖС–С— РҙС–Р»СҸСӮСҢ РҪавРҝС–Р» РҝСҖРҫСӮРёР»РөР¶РҪС– СҒСӮРҫСҖРҫРҪРё.
Дві РҫСҒС– СҒРёРјРөСӮСҖС–С— РҙС–Р»СҸСӮСҢ РҪавРҝС–Р» РҝСҖРҫСӮРёР»РөР¶РҪС– РәСғСӮРё.
ДіагРҫРҪалі РјР°СҺСӮСҢ РҫРҙРҪР°РәРҫРІСғ РҙРҫвжиРҪСғ.
ДіагРҫРҪалі РҝРөСҖРөСӮРёРҪР°СҺСӮСҢСҒСҸ РҝС–Рҙ РҝСҖСҸРјРёРј РәСғСӮРҫРј
РҹСҖСҸРјРҫРәСғСӮРҪРёРәами РјРҫР¶РҪР° замРҫСҒСӮРёСӮРё РҝР»РҫСүРёРҪСғ РұРөР· РҝСҖРҫРјС–Р¶РәС–РІ СӮР° РҪР°РәлаРҙРөРҪСҢ.
РӨРҫСҖРјСғла РҙР»СҸ РІРёР·РҪР°СҮРөРҪРҪСҸ РҝРөСҖРёРјРөСӮСҖР° РҝСҖСҸРјРҫРәСғСӮРҪРёРәР° РқРөхай РҝСҖСҸРјРҫРәСғСӮРҪРёРә РҗР’РЎР’ має РҙРҫвжиРҪСғ
ℓ
{\displaystyle \ell }
w
{\displaystyle w}
РҹР»РҫСүР°
S
=
ℓ
⋅
w
{\displaystyle S=\ell \cdot w\,}
РўР°РәРҫР¶ РҝР»РҫСүСғ РјРҫР¶РҪР° РІРёР·РҪР°СҮРёСӮРё Р·Р° С„РҫСҖРјСғР»РҫСҺ:
S
=
d
2
2
⋅
sin
φ
{\displaystyle S={\frac {d^{2}}{2}}\cdot \sin {\varphi }\,}
РҙРө
φ
{\displaystyle \varphi }
РҹРөСҖРёРјРөСӮСҖ
P
=
2
ℓ
+
2
w
=
2
(
ℓ
+
w
)
{\displaystyle P=2\ell +2w=2(\ell +w)\,}
Р”РҫвжиРҪР° РәРҫР¶РҪРҫС— РҙіагРҫРҪалі РҙРҫСҖС–РІРҪСҺРІР°СӮРёРјРө
d
=
ℓ
2
+
w
2
{\displaystyle d={\sqrt {\ell ^{2}+w^{2}}}}
Р Р°РҙС–СғСҒ РҫРҝРёСҒР°РҪРҫРіРҫ РәРҫла :
R
=
d
2
=
1
2
⋅
ℓ
2
+
w
2
{\displaystyle R={\frac {d}{2}}={\frac {1}{2}}\cdot {\sqrt {\ell ^{2}+w^{2}}}}
СҸРәСүРҫ
ℓ
=
w
{\displaystyle \ell =w\,}
РәРІР°РҙСҖР°СӮРҫРј . Р”РөСҸРәС– РјРөС…Р°РҪС–СҮРҪС– С…Р°СҖР°РәСӮРөСҖРёСҒСӮРёРәРё РҝР»РҫСҒРәРҫРіРҫ РҝРөСҖРөСҖС–Р·Сғ РҝСҖСҸРјРҫРәСғСӮРҪРҫС— С„РҫСҖРјРё:
ℓ
{\displaystyle \ell }
h вҖ” РІРёСҒРҫСӮР° РҝСҖСҸРјРҫРәСғСӮРҪРёРәР°.[ 11]
РңРҫРјРөРҪСӮРё С–РҪРөСҖСҶС–С— РҝР»РҫСҒРәРҫРіРҫ РҝРөСҖРөСҖС–Р·Сғ
РңРҫРјРөРҪСӮ С–РҪРөСҖСҶС–С—
J
x
{\displaystyle J_{x}}
x [ 12]
ℓ
⋅
h
3
12
{\displaystyle {\frac {\ell \cdot h^{3}}{12}}}
ℓ
⋅
h
3
3
{\displaystyle {\frac {\ell \cdot h^{3}}{3}}}
РңРҫРјРөРҪСӮ С–РҪРөСҖСҶС–С—
J
y
{\displaystyle J_{y}}
y [ 12]
ℓ
3
⋅
h
12
{\displaystyle {\frac {\ell ^{3}\cdot h}{12}}}
ℓ
3
⋅
h
3
{\displaystyle {\frac {\ell ^{3}\cdot h}{3}}}
Р’С–РҙСҶРөРҪСӮСҖРҫРІРёР№ РјРҫРјРөРҪСӮ С–РҪРөСҖСҶС–С—
J
x
y
{\displaystyle J_{xy}}
0
{\displaystyle 0}
−
ℓ
2
⋅
h
2
4
{\displaystyle -{\frac {\ell ^{2}\cdot h^{2}}{4}}}
РҹРҫР»СҸСҖРҪРёР№ РјРҫРјРөРҪСӮ С–РҪРөСҖСҶС–С—
J
p
{\displaystyle J_{p}}
ℓ
⋅
h
⋅
(
ℓ
2
+
h
2
)
12
{\displaystyle {\frac {\ell \cdot h\cdot (\ell ^{2}+h^{2})}{12}}}
ℓ
⋅
h
⋅
(
ℓ
2
+
h
2
)
3
{\displaystyle {\frac {\ell \cdot h\cdot (\ell ^{2}+h^{2})}{3}}}
Р Р°РҙС–СғСҒРё С–РҪРөСҖСҶС–С—
i
x
=
J
x
A
=
h
2
3
{\displaystyle i_{x}={\sqrt {\frac {J_{x}}{A}}}={\frac {h}{2{\sqrt {3}}}}}
i
y
=
J
y
A
=
ℓ
2
3
{\displaystyle i_{y}={\sqrt {\frac {J_{y}}{A}}}={\frac {\ell }{2{\sqrt {3}}}}}
i
x
=
h
3
{\displaystyle i_{x}={\frac {h}{\sqrt {3}}}}
i
y
=
ℓ
3
{\displaystyle i_{y}={\frac {\ell }{\sqrt {3}}}}
РһСҒСҢРҫРІРёР№ РјРҫРјРөРҪСӮ РҫРҝРҫСҖСғ
W
x
{\displaystyle W_{x}}
x
ℓ
⋅
h
2
6
{\displaystyle {\frac {\ell \cdot h^{2}}{6}}}
РңРҫРјРөРҪСӮ С–РҪРөСҖСҶС–С— РјР°СӮРөСҖіалСҢРҪРҫС— РҝлаСҒСӮРёРҪРё РҝСҖСҸРјРҫРәСғСӮРҪРҫС— С„РҫСҖРјРё СҲРёСҖРёРҪРҫСҺ
w
{\displaystyle w}
h РјР°СҒРҫСҺ m
I
c
=
h
2
+
w
2
12
⋅
m
{\displaystyle I_{c}={\frac {h^{2}+w^{2}}{12}}\cdot m\,\!}
[ 13]
РңРҫРјРөРҪСӮ С–РҪРөСҖСҶС–С— РјР°СӮРөСҖіалСҢРҪРҫС— РҝлаСҒСӮРёРҪРё РҝСҖСҸРјРҫРәСғСӮРҪРҫС— С„РҫСҖРјРё СҲРёСҖРёРҪРҫСҺ
w
{\displaystyle w}
h РјР°СҒРҫСҺ m
I
c
=
4
h
2
+
w
2
12
⋅
m
{\displaystyle I_{c}={\frac {4h^{2}+w^{2}}{12}}\cdot m\,\!}
РҶР·РҫРҝРөСҖРёРјРөСӮСҖРёСҮРҪР° РҪРөСҖС–РІРҪС–СҒСӮСҢ РҙР»СҸ РҝСҖСҸРјРҫРәСғСӮРҪРёРәС–РІ РҙРҫРІРҫРҙРёСӮСҢ, СүРҫ СҒРөСҖРөРҙ СғСҒС–С… РҝСҖСҸРјРҫРәСғСӮРҪРёРәС–РІ С–Р· Р·Р°РҙР°РҪРёРј РҝРөСҖРёРјРөСӮСҖРҫРј , РәРІР°РҙСҖР°СӮ РјР°СӮРёРјРө РҪайРұС–Р»СҢСҲСғ РҝР»РҫСүСғ .
РӣС–РҪС–С— РҝСҖРҫРІРөРҙРөРҪС– СҮРөСҖРөР· СҒРөСҖРөРҙРҪС– СӮРҫСҮРәРё СҒСӮРҫСҖС–РҪ РұСғРҙСҢ-СҸРәРҫРіРҫ СҮРҫСӮРёСҖРёРәСғСӮРҪРёРәР° С–Р· РҝРөСҖРҝРөРҪРҙРёРәСғР»СҸСҖРҪРёРјРё РҙіагРҫРҪалСҸРјРё СғСӮРІРҫСҖСҺСҺСӮСҢ РҝСҖСҸРјРҫРәСғСӮРҪРёРә.
РҹР°СҖалРөР»РҫРіСҖам С–Р· СҖС–РІРҪРёРјРё Р·Р° РҙРҫвжиРҪРҫСҺ РҙіагРҫРҪалСҸРјРё С” РҝСҖСҸРјРҫРәСғСӮРҪРёРәРҫРј.
РҜРҝРҫРҪСҒСҢРәР° СӮРөРҫСҖРөРјР° РҝСҖРҫ РІРҝРёСҒР°РҪРёР№ РІ РәРҫР»Рҫ СҮРҫСӮРёСҖРёРәСғСӮРҪРёРә [ 14]
РўРөРҫСҖРөРјР° РҝСҖРҫ Р‘СҖРёСӮР°РҪСҒСҢРәРёР№ РҝСҖР°РҝРҫСҖ [en] A , B , C , С– D , РҙР»СҸ РұСғРҙСҢ-СҸРәРҫС— СӮРҫСҮРәРё P РІ СӮС–Р№ СҒамій РҝР»РҫСүРёРҪС– РІ СҒРөСҖРөРҙРёРҪС– РҝСҖСҸРјРҫРәСғСӮРҪРёРәР° РұСғРҙРө РІРёРәРҫРҪСғРІР°СӮРёСҒСҸ СҖС–РІРҪС–СҒСӮСҢ:[ 15]
(
A
P
)
2
+
(
C
P
)
2
=
(
B
P
)
2
+
(
D
P
)
2
.
{\displaystyle \displaystyle (AP)^{2}+(CP)^{2}=(BP)^{2}+(DP)^{2}.}
РЎС…СҖРөСүРөРҪРёР№ РҝСҖСҸРјРҫРәСғСӮРҪРёРә (СӮР°РәРёР№, СүРҫ РҝРөСҖРөСӮРёРҪає СҒам СҒРөРұРө) СҒРәлаРҙаєСӮСҢСҒСҸ С–Р· РҙРІРҫС… РҝСҖРҫСӮРёР»РөР¶РҪРёС… СҒСӮРҫСҖС–РҪ Р·РІРёСҮайРҪРҫРіРҫ РҝСҖСҸРјРҫРәСғСӮРҪРёРәР° С– РҙРІРҫС… РҙіагРҫРҪалРөР№. РЎС…СҖРөСүРөРҪРёР№ РҝСҖСҸРјРҫРәСғСӮРҪРёРә, СӮР°Рә СҒамРҫ, С” СҖС–Р·РҪРҫРІРёРҙРҫРј СҒС…СҖРөСүРөРҪРҫРіРҫ СҮРҫСӮРёСҖРёРәСғСӮРҪРёРәР°. Р’С–РҪ має СӮРҫР№ СҒамий РҝРҫСҖСҸРҙРҫРә РІРөСҖСҲРёРҪ [en]
РЎС…СҖРөСүРөРҪРёР№ СҮРҫСӮРёСҖРёРәСғСӮРҪРёРә С–РҪРҫРҙС– Р°СҒРҫСҶС–СҺСҺСӮСҢ С–Р· РәСҖаваСӮРәРҫСҺ-РјРөСӮРөлиРәРҫРј Р°РұРҫ С„РҫСҖРјРҫСҺ РјРөСӮРөлиРәР° . РўСҖРёРІРёРјС–СҖРҪСғ РҝСҖСҸРјРҫРәСғСӮРҪСғ РәР°СҖРәР°СҒРҪСғ РәРҫРҪСҒСӮСҖСғРәСҶС–СҺ С–Р· РҙСҖРҫСӮСғ РјРҫР¶РҪР° СҒРәСҖСғСӮРёСӮРё СӮР°РәРёРј СҮРёРҪРҫРј, СүРҫ РІРҫРҪР° РҝСҖРёР№РјРө С„РҫСҖРјСғ РјРөСӮРөлиРәР°. РЎС…СҖРөСүРөРҪРёР№ РҝСҖСҸРјРҫРәСғСӮРҪРёРә С–РҪРҫРҙС– РҪазиваСҺСӮСҢ В«РәСғСӮРҫРІРҫСҺ РІС–СҒС–РјРәРҫСҺВ».
Р’РҪСғСӮСҖС–СҲРҪСҸ СҮР°СҒСӮРёРҪР° СҒС…СҖРөСүРөРҪРҫРіРҫ РҝСҖСҸРјРҫРәСғСӮРҪРёРәР° РјРҫР¶Рө РјР°СӮРё РҝРҫлігРҫРҪалСҢРҪСғ РіСғСҒСӮРёРҪСғ [en]
РЎС…СҖРөСүРөРҪРёР№ РҝСҖСҸРјРҫРәСғСӮРҪРёРә РҪРө С” СҖС–РІРҪРҫРәСғСӮРҪРёРј . РЎСғРјР° Р№РҫРіРҫ РІРҪСғСӮСҖС–СҲРҪС–С… РәСғСӮС–РІ (РҙРІРҫС… РіРҫСҒСӮСҖРёС… С– РҙРІРҫС… СҖРҫР·РіРҫСҖРҪСғСӮРёС… РәСғСӮС–РІ ), СҸРә С– РІ РұСғРҙСҢ-СҸРәРҫРіРҫ СҒС…СҖРөСүРөРҪРҫРіРҫ РҝСҖСҸРјРҫРәСғСӮРҪРёРәР°, РҙРҫСҖС–РІРҪСҺС” 720В°.[ 16]
РҹСҖСҸРјРҫРәСғСӮРҪРёРә С– СҒС…СҖРөСүРөРҪРёР№ РҝСҖСҸРјРҫРәСғСӮРҪРёРә С” СҮРҫСӮРёСҖРёРәСғСӮРҪРёРәами, СүРҫ РјР°СҺСӮСҢ РҪР°СҒСӮСғРҝРҪС– СҒРҝС–Р»СҢРҪС– влаСҒСӮРёРІРҫСҒСӮС–:
РЎС–РҙР»РҫРІРёР№ РҝСҖСҸРјРҫРәСғСӮРҪРёРә має 4 РҪРө РҝлаРҪР°СҖРҪС– РІРөСҖСҲРёРҪРё С– СғСӮРІРҫСҖРөРҪРёР№ СҮР°СҒСӮРәРҫРІРёРј СғСҒС–РәР°РҪРҪСҸРј [en] РҝСҖСҸРјРҫРәСғСӮРҪРҫРіРҫ РҝР°СҖалРөР»РөРҝС–РҝРөРҙР° , СүРҫ С” С”РҙРёРҪРҫСҺ РІРҪСғСӮСҖС–СҲРҪСҢРҫСҺ РјС–РҪімалСҢРҪРҫСҺ РҝРҫРІРөСҖС…РҪРөСҺ , СҸРәР° РІРёР·РҪР°СҮаєСӮСҢСҒСҸ СҸРә ліРҪС–Р№РҪР° РәРҫРјРұС–РҪР°СҶС–СҸ СҮРҫСӮРёСҖСҢРҫС… РІРөСҖСҲРёРҪ. РқР° малСҺРҪРәСғ РҝРҫРәазаРҪРҫ СҒРёРҪС–Рј РҝРҫРәазаРҪРҫ 4 СҖРөРұСҖР° РҝСҖСҸРјРҫРәСғСӮРҪРёРәР°, С– РҙРІС– РҙіагРҫРҪалі Р·РөР»РөРҪРёРј, РІСҒС– РІРҫРҪРё С” РҙіагРҫРҪалСҸРјРё РҝСҖСҸРјРҫРәСғСӮРҪРёС… РіСҖР°РҪРөР№ РҝР°СҖалРөР»РөРҝС–РҝРөРҙР°.РЈ СҒС„РөСҖРёСҮРҪС–Р№ РіРөРҫРјРөСӮСҖС–С— , СҒС„РөСҖРёСҮРҪРёРј РҝСҖСҸРјРҫРәСғСӮРҪРёРәРҫРј РҪазиваСҺСӮСҢ фігСғСҖСғ С–Р· СҮРҫСӮРёСҖРјР° СҖРөРұСҖами, СҸРәС– С” РҙСғгами РІРөлиРәРҫРіРҫ РәРҫла , СҸРәС– СғСӮРІРҫСҖСҺСҺСӮСҢ РҫРҙРҪР°РәРҫРІС– РәСғСӮРё РұС–Р»СҢСҲС– Р·Р° 90В°. РҹСҖРҫСӮРёР»РөР¶РҪС– РҙСғРіРё РјР°СҺСӮСҢ РҫРҙРҪР°РәРҫРІСғ РҙРҫвжиРҪСғ. РЎС„РөСҖРёСҮРҪР° РіРөРҫРјРөСӮСҖС–СҸ С” РҪайРҝСҖРҫСҒСӮС–СҲРҫСҺ С„РҫСҖРјРҫСҺ РөліРҝСӮРёСҮРҪРҫС— РіРөРҫРјРөСӮСҖС–С—. РҹРҫРІРөСҖС…РҪСҸ СҒС„РөСҖРё РІ ЕвРәліРҙРҫРІС–Р№ РіРөРҫРјРөСӮСҖС–С— С” РҪРө ЕвРәліРҙРҫРІРҫСҺ РҝРҫРІРөСҖС…РҪРөСҺ РІ СҖРҫР·СғРјС–РҪРҪС– РөліРҝСӮРёСҮРҪРҫС— РіРөРҫРјРөСӮСҖС–С—.
Р’ РөліРҝСӮРёСҮРҪС–Р№ РіРөРҫРјРөСӮСҖС–С— , РөліРҝСӮРёСҮРҪРёРј РҝСҖСҸРјРҫРәСғСӮРҪРёРәРҫРј С” фігСғСҖР° Сғ РөліРҝСӮРёСҮРҪС–Р№ РҝР»РҫСүРёРҪС–, СҮРҫСӮРёСҖРё СҖРөРұСҖР° СҸРәРҫС— С” РөліРҝСӮРёСҮРҪРёРјРё РҙСғгами, СҸРәС– СӮР°РәРҫР¶ СғСӮРІРҫСҖСҺСҺСӮСҢ РҫРҙРҪР°РәРҫРІС– РәСғСӮРё РұС–Р»СҢСҲС– Р·Р° 90В°. РҹСҖРҫСӮРёР»РөР¶РҪС– РҙСғРіРё РјР°СҺСӮСҢ РҫРҙРҪР°РәРҫРІСғ РҙРҫвжиРҪСғ.
РЈ РіС–РҝРөСҖРұРҫліСҮРҪС–Р№ РіРөРҫРјРөСӮСҖС–С— , РіС–РҝРөСҖРұРҫліСҮРҪРёРј РҝСҖСҸРјРҫРәСғСӮРҪРёРәРҫРј С” фігСғСҖР° РІ РіС–РҝРөСҖРұРҫліСҮРҪС–Р№ РҝР»РҫСүРёРҪС–, СҮРҫСӮРёСҖРё СҖРөРұСҖР° СҸРәРҫС— С” РіС–РҝРөСҖРұРҫліСҮРҪРёРјРё РҙСғгами, СҸРәС– СғСӮРІРҫСҖСҺСҺСӮСҢ РјС–Р¶ СҒРҫРұРҫСҺ РҫРҙРҪР°РәРҫРІС– РәСғСӮРё РјРөРҪСҲС– Р·Р° 90В°. РҹСҖРҫСӮРёР»РөР¶РҪС– РҙСғРіРё РјР°СҺСӮСҢ РҫРҙРҪР°РәРҫРІСғ РҙРҫвжиРҪСғ.
вҶ‘ РҡалиРҪРҫРІРёСҮ РӨ. Рҹ. РЎР»РҫРІРҪРёРә РјР°СӮРөРјР°СӮРёСҮРҪРҫС— СӮРөСҖРјС–РҪРҫР»РҫРіС–С—. (РҹСҖРҫС”РәСӮ).Р§. I. РўРөСҖРјС–РҪРҫР»РҫРіС–СҸ СҮРёСҒСӮРҫС— РјР°СӮРөРјР°СӮРёРәРё / Р—СҖРөРҙагСғвала РңР°СӮРөРјР°СӮРёСҮРҪР° РЎРөРәСҶС–СҸ РҹСҖРёСҖРҫРҙРҪРёСҮРҫРіРҫ РІС–РҙРҙС–Р»Сғ РҶРҪСҒСӮРёСӮСғСӮСғ РЈРәСҖаїРҪСҒСҢРәРҫС— РқР°СғРәРҫРІРҫС— РңРҫРІРё Р’РЈРҗРқ. вҖ” РҡРёС—РІ : Р”РөСҖжавРҪРө РІРёРҙавРҪРёСҶСӮРІРҫ РЈРәСҖаїРҪРё, 1925. вҖ” 128 СҒ.вҶ‘ Р° Рұ БілРҫРҙС–Рҙ РҶ.Рҡ. СӮР° С–РҪ. РЎР»РҫРІРҪРёРә СғРәСҖаїРҪСҒСҢРәРҫС— РјРҫРІРё РІ 11 СӮ. (1970-1980) / РҝС–Рҙ СҖРөРҙ. Р’РёРҪРҪРёРәР° Р’.Рһ., ЖайвРҫСҖРҫРҪРҫРәР° Р’.Р’. СӮР° С–РҪ. вҖ” РҡРёС—РІ : РқР°СғРәРҫРІР° РҙСғРјРәР°, 1977. вҖ” Рў. VIII [РҝСҖРёСҖМҒРҫРҙР° - СҖСҸС…СӮР»МҒРёРІРёР№]. вҖ” РЎ. 369.
вҶ‘ РҹР РҜРңРһРҡРЈРўРқРҳРҡ . РЎРӣРһР’РқРҳРҡ.ua .вҶ‘ Coxeter, Harold Scott MacDonald ; Longuet-Higgins, M.S.; Miller, J.C.P. (1954). Uniform polyhedra. Philosophical Transactions of the Royal Society of London. Series A. Mathematical and Physical Sciences . The Royal Society. 246 (916): 401вҖ”450. doi :10.1098/rsta.1954.0003 . ISSN 0080-4614 . JSTOR 91532 . MR 0062446 .вҶ‘ An Extended Classification of Quadrilaterals [РҗСҖС…С–РІРҫРІР°РҪРҫ 2019-12-30 Сғ Wayback Machine .] (An excerpt from De Villiers, M. 1996. Some Adventures in Euclidean Geometry. University of Durban-Westville.)вҶ‘ Zalman Usiskin and Jennifer Griffin, В«The Classification of Quadrilaterals. A Study of DefinitionВ», Information Age Publishing, 2008, pp. 34вҖ“36 ISBN 1-59311-695-0 .
вҶ‘ Owen Byer; Felix Lazebnik; Deirdre L. Smeltzer (19 СҒРөСҖРҝРҪСҸ 2010). Methods for Euclidean Geometry ISBN 978-0-88385-763-2 . РҹСҖРҫСҶРёСӮРҫРІР°РҪРҫ 13 лиСҒСӮРҫРҝР°РҙР° 2011 . вҶ‘ РҹСҖСҸРјРҫРәСғСӮРҪРёРә. РӨРҫСҖРјСғли СӮР° влаСҒСӮРёРІРҫСҒСӮС– РҝСҖСҸРјРҫРәСғСӮРҪРёРәР° вҶ‘ Michael De Villiers. Generalizing Van Aubel Using Duality // Mathematics Magazine 73 (4). вҖ” Oct. 2000. вҖ” РЎ. 303вҖ“307 . вҖ” DOI :10.1080/0025570X.2000.11996859
вҶ‘ Rectangular mechanical properties . www.wolframalpha.com (Р°РҪРіР».) .вҶ‘ Р° Рұ Rectangular area . eFunda engineering Fundamentals (Р°РҪРіР».) . eFunda.вҶ‘ Raymond A. Serway (1986). Physics for Scientists and Engineers, second ed 202 . ISBN 0-03-004534-7 вҶ‘ Cyclic Quadrilateral Incentre-Rectangle [РҗСҖС…С–РІРҫРІР°РҪРҫ 28 РІРөСҖРөСҒРҪСҸ 2011 Сғ Wayback Machine .] with interactive animation illustrating a rectangle that becomes a 'crossed rectangle', making a good case for regarding a 'crossed rectangle' as a type of rectangle.вҶ‘ Hall, Leon M. & Robert P. Roe (1998). An Unexpected Maximum in a Family of Rectangles (PDF) . Mathematics Magazine . 71 (4): 285вҖ”291. JSTOR 2690700 . вҶ‘ Michael De Villiers. Stars: A Second Look // Mathematics in School, 28(5). вҖ” 1999. РҗСҖС…С–РІРҫРІР°РҪРҫ Р· РҙР¶РөСҖРөла 3 РұРөСҖРөР·РҪСҸ 2016. РҹСҖРҫСҶРёСӮРҫРІР°РҪРҫ 2024-06-22.