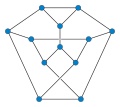
Граф Тітце

Граф Тітце
Названо на честь	Генріха Франца Фрідріха Тітце
Вершин	12
Ребер	18
Радіус	3
Діаметр	3
Обхват	3
Автоморфізм	12 (D6)
Хроматичне число	3
Хроматичний індекс	4
Властивості	Кубічний Снарк

Розбиття стрічки Мебіуса на шість взаємно дотичних областей. Вершини і ребра розбиття утворюють вкладення графу Тітце в стрічку.

В теорії графів граф Титце — це неорієнтований кубічний граф з 12 вершинами і 18 ребрами. Граф названий ім'ям Генріха Франца Фрідріха Тітце, який показав в 1910 році, що стрічку Мебіуса можна розділити на шість областей, що дотикаються одна одної — три уздовж кордону стрічки і три уздовж центральної лінії — а тому для графів, що допускають вкладення в стрічку Мебіуса, може знадобитися шість кольорів.[1] Граничні сегменти областей Тітце поділу стрічки Мебіуса (включаючи сегменти уздовж кордону самої стрічки) утворюють вкладення графу Тітце.

Зв'язок з графом Петерсена

Граф Тітце можна отримати з графу Петерсена заміною однієї з його вершин трикутником.[2][3] Подібно графу Тітце граф Петерсена слугує межами шести взаємно дотичних областей, але в проективній площині, а не на стрічці Мебіуса. Якщо вирізати околицю деякої вершини цього розбиття проективної площини, вершина замінюється межами цієї діри, що дає в точності побудову графу Тітце, описану вище.

Гамільтоновість

І граф Тітце, і граф Петерсена максимально негамільтонові — вони не мають гамільтонова циклу, але будь-які дві несуміжні вершини можуть бути з'єднані гамільтоновим шляхом.[2] Граф Тітце і граф Петерсена є 2-вершинно-зв'язними кубічними негамільтоновими графами з 12 або меншою кількістю вершин.[4]

На відміну від графу Петерсена, граф Тітце не є гіпогамільтоновим — видалення однієї з трьох вершин трикутника утворює менший граф, що залишається гамільтоновим.

Розмальовка ребер і досконалі паросполучення

Розфарбовування ребер графу Тітце вимагає чотирьох кольорів, тобто його хроматичний індекс дорівнює 4. Це еквівалентно тому, що ребра графу Тітце можуть бути розділені на чотири паросполучення, але не менше.

Граф Тітце задовольняє частині вимог визначення снарка — він є кубічним графом без мостів і його ребра не можуть бути пофарбовані в 3 кольори. Однак деякі автори обмежують снарків графами без 3-циклів і 4-циклів, а при цих сильніших умовах граф Тітце не є снарком. Граф Тітце ізоморфний графу J₃, графу з нескінченного сімейства снарків «Квітка», запропонованих Р. Ісаакксом у 1975 році .[5]

На відміну від графу Петерсена, граф Тітце може бути покритий чотирма досконалими паросполученнями. Це властивість грає ключову роль в доведенні, що перевірка, чи можна покрити граф чотирма паросполученнями, є NP-повною задачею.[6]

Додаткові властивості

Граф Тітце має хроматичне число 3, хроматичний індекс 4, обхват 3 і діаметр 3. Його число незалежності дорівнює 5, а група автоморфізмів має порядок 12 і вона ізоморфна діедральній групі D₆, групи симетрій шестикутника, що включає як обертання, так і відбивання. Ця група містить дві орбіти розміру 3 і одну розміру 6 на вершинах, а тому цей граф не вершинно-транзитивний.

Примітки

1. Tietze, Heinrich (1910), Einige Bemerkungen zum Problem des Kartenfärbens auf einseitigen Flächen [Some remarks on the problem of map coloring on one-sided surfaces], DMV Annual Report, 19: 155—159^[недоступне посилання з квітня 2019].
2. Clark, L.; Entringer, R. (1983), Smallest maximally nonhamiltonian graphs, Periodica Mathematica Hungarica, 14 (1): 57—68, doi:10.1007/BF02023582
3. Weisstein, Eric W. Tietze's Graph(англ.) на сайті Wolfram MathWorld.
4. Punnim, Narong; Saenpholphat, Varaporn; Thaithae, Sermsri (2007), Almost Hamiltonian cubic graphs (PDF), International Journal of Computer Science and Network Security, 7 (1): 83—86, архів оригіналу (PDF) за 22 листопада 2010, процитовано 5 червня 2016
5. Isaacs, R. (1975), Infinite families of nontrivial trivalent graphs which are not Tait colorable, Amer. Math. Monthly, Mathematical Association of America, 82 (3): 221—239, doi:10.2307/2319844, JSTOR 2319844.
6. Esperet, L.; Mazzuoccolo, G. (2014), On cubic bridgeless graphs whose edge-set cannot be covered by four perfect matchings, Journal of Graph Theory, 77 (2): 144—157, arXiv:1301.6926, doi:10.1002/jgt.21778, MR 3246172.

Галерея

• 
  Хроматичне число графу Тітце дорівнює 3.
• 
  Хроматичний індекс графу Тітце дорівнює 4.
• 
  Граф Тітце має число перетинів 2 і він 1-планарний
• 
  Тривимірне вкладення графу Тітце.