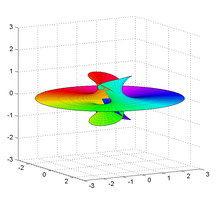
Поверхность Ричмонда для m=2. Поверхность Ричмонда — минимальная поверхность , впервые описанная английским математиком Гербертом Уильямом Ричмондом в 1904 году[ 1] концом и одним самопересекающимся концом как у поверхности Эннепера .
Поверхность имеет параметризацию Вейерштрасса — Эннепера
f
(
z
)
=
1
/
z
2
,
g
(
z
)
=
z
m
{\displaystyle f(z)=1/z^{2},g(z)=z^{m}}
X
(
z
)
=
ℜ
[
(
−
1
/
2
z
)
−
z
2
m
+
1
/
(
4
m
+
2
)
]
Y
(
z
)
=
ℜ
[
(
−
i
/
2
z
)
+
i
z
2
m
+
1
/
(
4
m
+
2
)
]
Z
(
z
)
=
ℜ
[
z
m
/
m
]
{\displaystyle {\begin{aligned}X(z)&=\Re [(-1/2z)-z^{2m+1}/(4m+2)]\\Y(z)&=\Re [(-i/2z)+iz^{2m+1}/(4m+2)]\\Z(z)&=\Re [z^{m}/m]\end{aligned}}}
Ассоциированным семейством поверхности является просто вращение поверхности вокруг оси z.
Принимая m = 2, получаем вещественное параметрическое выражение[ 2]
X
(
u
,
v
)
=
(
1
/
3
)
u
3
−
u
v
2
+
u
u
2
+
v
2
Y
(
u
,
v
)
=
−
u
2
v
+
(
1
/
3
)
v
3
−
v
u
2
+
v
2
Z
(
u
,
v
)
=
2
u
{\displaystyle {\begin{aligned}X(u,v)&=(1/3)u^{3}-uv^{2}+{\frac {u}{u^{2}+v^{2}}}\\Y(u,v)&=-u^{2}v+(1/3)v^{3}-{\frac {v}{u^{2}+v^{2}}}\\Z(u,v)&=2u\end{aligned}}}
Jesse Douglas, Tibor Radó. The Problem of Plateau: A Tribute to Jesse Douglas & Tibor Radó // World Scientific. — 1992.John Oprea. The Mathematics of Soap Films: Explorations With Maple. — American Mathematical Soc., 2000.

![{\displaystyle {\begin{aligned}X(z)&=\Re [(-1/2z)-z^{2m+1}/(4m+2)]\\Y(z)&=\Re [(-i/2z)+iz^{2m+1}/(4m+2)]\\Z(z)&=\Re [z^{m}/m]\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/934419d302c2d08a3baa55573a5e858bfa3615aa)

