|
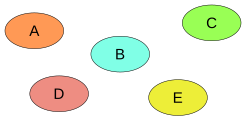
Непересекающиеся множества В математике говорят, что два множества не пересекаются или дизъюнктны, если у них нет общих элементов. Эквивалентно, непересекающиеся множества — это множества, пересечение которых является пустым множеством[1]. Например, {1, 2, 3} и {4, 5, 6} непересекающиеся множества, в то время как {1, 2, 3} и {3, 4, 5} таковыми не являются. Обобщения Приведённое определение непересекающихся множеств может быть расширено на любое семейство множеств[англ.]*. Семейство множеств попарно дизъюнктно (элементы попарно не пересекаются), если любые два множества в семействе не имеют общих элементов[1]. Например, набор множеств { {1}, {2}, {3}, ... } попарно дизъюнктен. Говорят, что два множества почти не пересекаются[англ.], если их пересечение в некотором смысле мало. Например, два бесконечных множества, пересечение которых является конечным множеством, можно считать почти не пересекающимися[2]. В топологии существуют различные обозначения разделённых множеств с более строгими условиями, чем отсутствие пересечения. Например, два множества считаются разделимыми, когда они имеют непересекающиеся замыкания или непересекающиеся окрестности. Подобно этому, в метрическом пространстве положительно разделённые множества[англ.] — это множества, разделённые ненулевым расстоянием[3]. Примеры
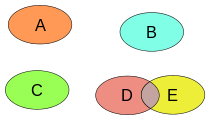
ПересеченияДизъюнктность множеств или семейств множеств можно выразить в терминах пересечений. Два множества A и B дизъюнктны тогда и только тогда, когда их пересечение является пустым множеством[1]. Из этого определения следует, что любое множество дизъюнктно с пустым множеством и пустое множество является единственным множеством, дизъюнктным самому себе[4]. Семейство F множеств попарно дизъюнктно, если для любых двух множеств в семействе их пересечение пусто[1]. Если семейство содержит более одного множества, отсюда следует, что пересечение всех множеств семейства пусто. Однако семейство, состоящее из одного множества, по определению является «попарно дизъюнктным» и очевидно может иметь непустое пересечение. Кроме того, семейство множеств может иметь пустое пересечение, но не быть попарно дизъюнктно[5]. Например, три множества { {1, 2}, {2, 3}, {1, 3} } имеют пустое пересечение, но они не попарно дизъюнктны. Фактически нет двух дизъюнктных множеств в этом наборе. Также пустое семейство множеств является попарно дизъюнктным[6]. Семейство Хелли — это система множеств, в которой только подсемейства с пустым пересечением попарно дизъюнктны. Например, замкнутые интервалы на вещественной оси образуют семейство Хелли — если семейство замкнутых интервалов имеет пустое пересечение и минимально (то есть никакое подсемейство не имеет пустое пересечение), оно должно быть попарно дизъюнктно[7]. Дизъюнктные объединения и разбиенияРазбиение множества X — это любой набор взаимно дизъюнктных множеств, объединение которых равно X[8]. Любое разбиение можно эквивалентно описать отношением эквивалентности, бинарным отношением, определяющим, принадлежат два элемента одному и тому же множеству в разложении или нет[8]. Системы непересекающихся множеств[9] и измельчение разбиения[англ.][10] — две техники в информатике для эффективной работы с разбиениями набора объектов, соответственно, для операции объединения, которая сливает вместе два множества, и операции измельчения, которая разбивает одно множество на два. Дизъюнктное объединение может означать две вещи. В наиболее простом случае это может означать объединение дизъюнктных множеств[11]. Но если два или более множеств не дизъюнктны, их дизъюнктное объединение может быть образовано путём модификации множеств[12][13]. Например, два множества могут быть сделаны дизъюнктыми путём замены элементов упорядоченными парами элемента и индекса, определяющего, какому множеству принадлежит элемент – первому или второму[14]. Та же техника может быть применена для семейств из более чем двух множеств[15]. См. также
Примечания
Литература
Ссылки
|
Portal di Ensiklopedia Dunia