Алгоритм Эдмондса — Карпа

Алгоритм Эдмондса — Карпа решает задачу нахождения максимального потока в транспортной сети. Алгоритм представляет собой частный случай метода Форда — Фалкерсона и работает за время ${\displaystyle O(|V|\cdot |E|^{2})}$ в графе ${\displaystyle G=(V,E)}$. Впервые был опубликован в 1970 году советским учёным Е. А. Диницом. Позже, в 1972 году, был независимо открыт Эдмондсом и Карпом.

Алгоритм

Алгоритм Эдмондса — Карпа — это вариант алгоритма Форда — Фалкерсона, при котором на каждом шаге выбирают кратчайший дополняющий путь из ${\displaystyle s}$ в ${\displaystyle t}$ в остаточной сети (полагая, что каждое ребро имеет единичную длину). Кратчайший путь находится поиском в ширину.

Описание

1. Обнуляем все потоки. Остаточная сеть изначально совпадает с исходной сетью.
2. В остаточной сети находим кратчайший путь из источника в сток. Если такого пути нет, останавливаемся.
3. Пускаем через найденный путь (он называется увеличивающим путём или увеличивающей цепью) максимально возможный поток:
   1. На найденном пути в остаточной сети ищем ребро с минимальной пропускной способностью ${\displaystyle c_{\min }}$.
   2. Для каждого ребра на найденном пути увеличиваем поток на ${\displaystyle c_{\min }}$, а в противоположном ему — уменьшаем на ${\displaystyle c_{\min }}$.
   3. Модифицируем остаточную сеть. Для всех рёбер на найденном пути, а также для противоположных им рёбер, вычисляем новую пропускную способность. Если она стала ненулевой, добавляем ребро к остаточной сети, а если обнулилась, стираем его.
4. Возвращаемся на шаг 2.

Чтобы найти кратчайший путь в графе, используем поиск в ширину:

1. Создаём очередь вершин О. Вначале О состоит из единственной вершины s.
2. Отмечаем вершину s как посещённую, без родителя, а все остальные как непосещённые.
3. Пока очередь не пуста, выполняем следующие шаги:
   1. Удаляем первую в очереди вершину u.
   2. Для всех дуг (u, v), исходящих из вершины u, для которых вершина v ещё не посещена, выполняем следующие шаги:
      1. Отмечаем вершину v как посещённую, с родителем u.
      2. Добавляем вершину v в конец очереди.
      3. Если v = t, выходим из обоих циклов: мы нашли кратчайший путь.
4. Если очередь пуста, возвращаем ответ, что пути нет вообще и останавливаемся.
5. Если нет, идём от t к s, каждый раз переходя к родителю. Возвращаем путь в обратном порядке.

Сложность

В процессе работы алгоритм Эдмондса — Карпа будет находить каждый дополняющий путь за время ${\displaystyle O(|E|)}$. Ниже мы докажем, что общее число увеличений потока, выполняемое данным алгоритмом, составляет ${\displaystyle O(|V|\cdot |E|)}$. Таким образом, сложность алгоритма Эдмондса — Карпа равна ${\displaystyle O(|V|\cdot |E|^{2})}$.

Доказательство

Назовём расстоянием от вершины x до вершины у длину кратчайшего пути от x до y в остаточной сети, измеряемую числом рёбер. Если такого пути нет, будем считать расстояние бесконечным. Будем говорить, что y приблизилась к x (отдалилась от x), если расстояние от x до y уменьшилось (увеличилось). Будем говорить, что y ближе к x (дальше от x), чем z, если расстояние от x до y меньше (больше), чем расстояние от x до z.

Лемма. В ходе работы алгоритма ни одна вершина никогда не приближается к источнику. Доказательство. Пусть это не так, тогда при каком-то увеличении потока некоторые вершины приблизились к источнику. Назовём их неправильными. Выберем ту из неправильных вершин, которая после увеличения потока оказалась ближе всех к источнику (если таких больше одной, то любую из них). Обозначим выбранную вершину через v. Рассмотрим кратчайший путь от s до v. Обозначим предпоследнюю вершину на этом пути через u, таким образом, путь имеет вид ${\displaystyle s-\ldots -u-v}$. Поскольку u ближе к s, чем v, а v — ближайшая к s из неправильных вершин, то u — вершина правильная. Обозначив расстояния от s до u и v до и после увеличения потока соответственно через ${\displaystyle d_{u}\ }$, ${\displaystyle d_{u}^{'}}$, ${\displaystyle d_{v}\ }$, ${\displaystyle d_{v}^{'}}$, имеем:

${\displaystyle d_{v}^{'}<d_{v}}$

${\displaystyle d_{u}^{'}\geq d_{u}}$

${\displaystyle d_{v}^{'}=d_{u}^{'}+1}$,

откуда

${\displaystyle d_{v}\geq d_{u}+2}$

Следовательно, до увеличения потока дуга (u, v) отсутствовала в остаточной сети. Чтобы оно появилось, увеличивающий путь должен был содержать дугу (v, u). Но в алгоритме Эдмондса — Карпа увеличивающий путь всегда кратчайший, следовательно,

${\displaystyle d_{v}=d_{u}-1}$,

что противоречит предыдущему неравенству. Значит, наше предположение было неверным. Лемма доказана.

Назовём критическим то из рёбер увеличивающего пути, у которого остаточная пропускная способность минимальна. Оценим, сколько раз некое ребро (u, v) может оказываться критическим. Пускай это произошло на итерации ${\displaystyle t_{1}}$, а в следующий раз на итерации ${\displaystyle t_{2}}$. Обозначая через ${\displaystyle D_{y}(t)}$ расстояние от s до y на итерации t, имеем:

${\displaystyle D_{v}(t_{1})=D_{u}(t_{1})+1}$

${\displaystyle D_{v}(t_{2})=D_{u}(t_{2})+1}$

Заметим, что на итерации ${\displaystyle t_{1}}$ критическое ребро исчезает из остаточной сети. Чтобы к моменту итерации ${\displaystyle t_{2}}$ ребро (u, v) в ней вновь появилось, необходимо, чтобы на какой-то промежуточной итерации ${\displaystyle t_{3}}$ был выбран увеличивающий путь, содержащий ребро (v, u). Следовательно,

${\displaystyle D_{u}(t_{3})=D_{v}(t_{3})+1}$

Используя ранее доказанную лемму, получаем:

${\displaystyle D_{v}(t_{2})=D_{u}(t_{2})+1\geq D_{u}(t_{3})+1=D_{v}(t_{3})+2\geq D_{v}(t_{1})+2}$

Поскольку изначально ${\displaystyle D_{v}>0}$ (иначе v = s, но ребро, ведущее в s, не может появиться на кратчайшем пути из s в t), и всегда, когда ${\displaystyle D_{v}}$ конечно, оно меньше |V| (кратчайший путь не содержит циклов, и, следовательно, содержит менее |V| рёбер), ребро может оказаться критическим не более ${\displaystyle {\frac {(|V|-1)-1}{2}}+1=|V|/2}$ раз. Поскольку каждый увеличивающий путь содержит хотя бы одно критическое ребро, а всего рёбер, которые могут когда-то стать критическими, ${\displaystyle 2|E|}$ (все рёбра исходной сети и им противоположные), то мы можем увеличить путь не более |Е|·|V| раз. Следовательно, число итераций не превышает O(|E|·|V|), что и требовалось доказать.

Пример

Пусть задана сеть с истоком в вершине ${\displaystyle A}$ и стоком в вершине ${\displaystyle G}$. На рисунке парой ${\displaystyle f/c}$ обозначен поток по этому ребру и его пропускная способность.

Поиск в ширину

Опишем поиск в ширину на первом шаге.

1. Очередь состоит из единственной вершины A. Посещена вершина A. Родителя нет.
2. Очередь состоит (от начала к концу) из вершин B и D. Посещены вершины A, B, D. Вершины B, D имеют родителя А.
3. Очередь состоит из вершин D и C. Посещены A, B, C, D. Вершины B, D имеют родителя А, вершина C — родителя B.
4. Очередь состоит из вершин C, E, F. Посещены A, B, C, D, E, F. Вершины B, D имеют родителя А, вершина C — родителя B, вершины E, F — родителя D.
5. Вершина C удаляется из очереди: рёбра из неё ведут только в уже посещённые вершины.
6. Обнаруживается ребро (E,G) и цикл останавливается. В очереди вершины (F,G). Посещены все вершины. Вершины B,D имеют родителя А, вершина C — родителя B, вершины E,F — родителя D, вершина G — родителя E.
7. Идём по родителя: ${\displaystyle G\to E\to D\to A}$. Возвращаем пройденный путь в обратном порядке: ${\displaystyle A\to D\to E\to G}$.

Заметим, что в очередь последовательно добавляли вершины, достижимые из A ровно за 1 шаг, ровно за 2 шага, ровно за 3 шага. Кроме того, родителем каждой вершины является вершина, достижимая из A ровно на 1 шаг быстрее.

Основной алгоритм

Пропускная способность пути	Путь
${\displaystyle \min(c_{f}(A,D),c_{f}(D,E),c_{f}(E,G))=}$ ${\displaystyle \min(3-0,2-0,1-0)=}$ ${\displaystyle \min(3,2,1)=1}$	${\displaystyle A,D,E,G}$
${\displaystyle \min(c_{f}(A,D),c_{f}(D,F),c_{f}(F,G))=}$ ${\displaystyle \min(3-1,6-0,9-0)=}$ ${\displaystyle \min(2,6,9)=2}$	${\displaystyle A,D,F,G}$
${\displaystyle \min(c_{f}(A,B),c_{f}(B,C),c_{f}(C,D),c_{f}(D,F),c_{f}(F,G))=}$ ${\displaystyle \min(3-0,4-0,1-0,6-2,9-2)=}$ ${\displaystyle \min(3,4,1,4,7)=1}$	${\displaystyle A,B,C,D,F,G}$
${\displaystyle \min(c_{f}(A,B),c_{f}(B,C),c_{f}(C,E),c_{f}(E,D),c_{f}(D,F),c_{f}(F,G))=}$ ${\displaystyle \min(3-1,4-1,2-0,0--1,6-3,9-3)=}$ ${\displaystyle \min(2,3,2,1,3,6)=1}$	${\displaystyle A,B,C,E,D,F,G}$

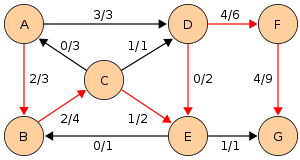Отметим, что в процессе выполнения алгоритма длины дополняющих путей (на рисунках обозначены красным) не убывают. Это свойство выполняется благодаря тому, что мы ищем кратчайший дополняющий путь.

Алгоритм Диница

Основная статья: Алгоритм Диница

Улучшенной версией алгоритма Эдмондса-Карпа является алгоритм Диница, требующий ${\displaystyle O(|V|^{2}|E|)}$ операций.

Назовём вспомогательной бесконтурной сетью графа G с источником s его подграф, содержащий только такие рёбра (u, v), для которых минимальное расстояние от s до v на единицу больше минимального расстояния от s до u.

Алгоритм Диница:

1. Строим минимальную бесконтурную сеть остаточного графа.
2. Пока в сети есть путь из s в t, выполнить следующие шаги:
   1. Находим кратчайший путь из s в t. Если его нет, выйти из цикла.
   2. На найденном пути в остаточной сети ищем ребро с минимальной пропускной способностью ${\displaystyle c_{\min }}$.
   3. Для каждого ребра на найденном пути увеличиваем поток на ${\displaystyle c_{\min }}$, а в противоположном ему — уменьшаем на ${\displaystyle c_{\min }}$.
   4. Удаляем все рёбра, достигшие насыщения.
   5. Удаляем все тупики (то есть вершины, кроме стока, откуда не выходит рёбер, и вершины, кроме источника, куда рёбер не входит) вместе со всеми инцидентными им рёбрами.
   6. Повторяем предыдущий шаг, пока есть что удалять.
3. Если найденный поток ненулевой, добавляем его к общему потоку и возвращаемся на шаг 1.

Ссылки

• Визуализация алгоритма
• Реализация поиска максимального потока методом Эдмондса-Карпа на Java

Литература

• Томас Кормен и др. Алгоритмы: построение и анализ = INTRODUCTION TO ALGORITHMS. — 2-е изд. — М.: «Вильямс», 2006. — С. 1296. — ISBN 0-07-013151-1.