物理学 において、ルンゲ=レンツベクトル (英 : Runge–Lenz vector )とは、ケプラー問題 、すなわち逆二乗則 に従う中心力 の下の運動における保存量 の一つ。古典力学 の天体運行 のケプラー問題や量子力学 の水素原子モデルの問題 などに現れる。空間的な回転対称性 の下で保存量となる角運動量 のように、他の多くの保存量が幾何学的な対称性 から導かれるのとは異なり、ルンゲ=レンツベクトルを導く対称性 は力学的性質に由来し、力学的対称性と呼ばれる。水素原子の束縛状態 においては、量子力学的な角運動量演算子 とルンゲ=レンツベクトル演算子の交換関係 は4次特殊直交群 SO(4) に対応するリー代数 をなし、固有値問題 の代数的な解法を与える。
ルンゲ=レンツベクトルという名はドイツの物理学者カール・ルンゲ とヴィルヘルム・レンツ (英語版 ) [ 4] 1924年 の前期量子論 の論文において、レンツはケプラー問題の摂動 にルンゲ=レンツベクトルを適用し、その引用文献として、ルンゲのベクトル解析 の著作 "Vectoranalysis " を挙げた[ 5] [ 6] ピエール=シモン・ラプラス はルンゲやレンツに先駆けて、1799年 の天体力学 の著作 "Traité de mécanique céleste " の中でルンゲ=レンツベクトルの性質を論じており[ 4] [ 7] [ 8] ラプラス=ルンゲ=レンツベクトル (英 : Laplace–Runge–Lenz vector )とも呼ばれる。但し、その発見はさらに古く、少なくとも18世紀初頭のベルヌーイ家 の門弟ヤコブ・ヘルマン (英語版 ) ヨハン・ベルヌーイ の結果に遡るとされる[ 9]
ルンゲ=レンツベクトルは距離に反比例する引力 型の中心力ポテンシャルによるケプラー問題に現れる。重力ポテンシャル によって太陽 の回りを運行する惑星 やクーロンポテンシャル によって原子核 の回りを運動する水素型原子の電子 の運動はそうした例である。ここで、古典力学でのケプラー問題を考え、ルンゲ=レンツベクトルを導入する。惑星や電子の質量に対し、太陽や原子核の質量は十分大きく、その運動は無視できるとし、原点に固定されているものと仮定する[ 注 1] 質点 の位置座標を r m とし、原点を中心とした中心力ポテンシャルを
V
(
r
)
=
−
k
r
(
k
>
0
)
{\displaystyle V(r)=-{\frac {k}{r}}\quad (k>0)}
とする。正の定数 k は、重力ポテンシャルの下での天体運行モデルの場合、太陽の質量を M 、惑星の質量を m とすれば、万有引力定数 G により、k = GMm Z 、電気素量 e と真空の誘電率 ε 0 k = Ze 2 /4πε 0 [ 注 2] 運動方程式 は
p
˙
=
−
∇
V
(
r
)
=
−
k
r
2
r
r
{\displaystyle {\dot {\boldsymbol {p}}}=-\nabla V(r)=-{\frac {k}{r^{2}}}{\frac {\boldsymbol {r}}{r}}}
となる。但し、ドット記号は時間微分 を表し、p 運動量
p
=
m
r
˙
{\displaystyle {\boldsymbol {p}}=m{\dot {\boldsymbol {r}}}}
である。運動方程式の右辺は逆二乗則 に従う中心力 を表している。
この系では、力学的エネルギー
E
=
m
r
˙
2
2
+
V
(
r
)
{\displaystyle E={\frac {m{\dot {\boldsymbol {r}}}^{2}}{2}}+V(r)}
と角運動量ベクトル
L
=
r
×
p
{\displaystyle {\boldsymbol {L}}={\boldsymbol {r}}\times {\boldsymbol {p}}}
は時間に対して不変な保存量となる。ここで、質点は角運動量ベクトルに垂直となる平面内を運動し、その軌道は原点を焦点 とする二次曲線 となる。特に E < 0楕円軌道 となる。楕円軌道の軌道長半径 を a 、軌道離心率 を e とすると
E
=
−
k
2
a
{\displaystyle E=-{\frac {k}{2a}}}
L
=
m
k
a
(
1
−
e
2
)
(
L
=
|
L
|
)
{\displaystyle L={\sqrt {mka(1-e^{2})}}\quad (L=|{\boldsymbol {L}}|)}
の関係が成り立つ[ 注 3]
このとき、
A
=
p
×
L
−
m
k
r
r
{\displaystyle {\boldsymbol {A}}={\boldsymbol {p}}\times {\boldsymbol {L}}-mk{\frac {\boldsymbol {r}}{r}}}
で定義されるベクトルをルンゲ=レンツベクトル と呼ぶ[ 注 4]
A
˙
=
0
{\displaystyle {\dot {\boldsymbol {A}}}={\boldsymbol {0}}}
を満たす保存量である。
一般に中心力ポテンシャルの下での運動は回転対称性 から角運動量ベクトルは保存量となり、その軌道は角運動量ベクトルに垂直な一定平面内に限られる。一方で、必ずも軌道が閉じて閉軌道 となることは保証されない[ 注 5] V (r )近日点 と遠日点 を結ぶ軸に歳差 が生じ、楕円軌道としては閉じない。軌道が閉じる背後には角運動量ベクトルに加えて、別の保存量の存在が示唆されるが、ルンゲ=レンツベクトルがその保存量となっている。
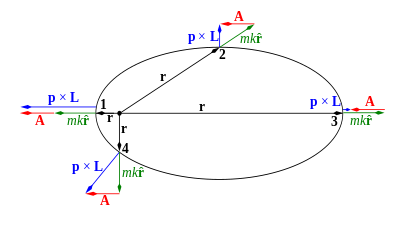
楕円軌道の各点におけるルンゲ=レンツベクトル A p L mkr / r r p mke である。参考に p L mkr / r ˆ r r / r ルンゲ=レンツベクトルは時間的に変化しない一定ベクトルであり、楕円軌道を含む一定平面内に位置する。その方向は原点である焦点と近日点 (perihelion ) を結ぶ方向にある。また、その大きさは
A
=
m
k
e
{\displaystyle A=mke}
で与えられる。従って、近日点の座標を r p
A
=
m
k
e
r
p
r
p
{\displaystyle {\boldsymbol {A}}=mke{\frac {{\boldsymbol {r}}_{p}}{r_{p}}}}
と表すことができる。ルンゲ=レンツベクトルを mk で除したベクトル
e
=
A
m
k
{\displaystyle {\boldsymbol {e}}={\frac {\boldsymbol {A}}{mk}}}
は大きさが軌道離心率 e である一定ベクトルである。このベクトルは離心率ベクトル と呼ばれる。
ある時刻 t における系の状態は、位置座標 r x , y , z )p px , py , pz )相空間 の点として記述され、その時間発展は相空間上の軌道を描く。一般に保存量が存在すれば、相空間の軌道は制限され、自由度が下がる。特に相空間の次元を 2n とすると n 個の独立な保存量が存在すれば、相空間上の軌道は完全に決定される[ 注 6] 直交 しており、
A
⋅
L
=
0
{\displaystyle {\boldsymbol {A}}\cdot {\boldsymbol {L}}={\boldsymbol {0}}}
を満たす。また、ルンゲ=レンツベクトル、角運動量ベクトル、エネルギーは関係式
A
2
=
m
2
k
2
+
2
m
E
L
2
{\displaystyle A^{2}=m^{2}k^{2}+2mEL^{2}}
で結ばれている。
ルンゲ=レンツベクトルという名はドイツの物理学者カール・ルンゲ とヴィルヘルム・レンツ (英語版 ) 前期量子論 でケプラー問題 を扱った1924年の論文の中で、エネルギー準位 の摂動にルンゲ=レンツベクトルを適用した[ 5] Vectoranalysis " を挙げた。ルンゲはその著作において、ベクトルが関わる微積分 を扱った章で、中心力の下での運動では角運動量が保存量となることを示した後、距離の2乗に反比例する中心力では別の定ベクトルが存在し、逆にその定ベクトルから軌道の方程式が導かれることを記している[ 6] ヴォルフガング・パウリ は、1926年の論文で当時、原子構造 を説明する新しい理論として発展しつつあった行列力学 を水素原子に適用し、その中でレンツの結果を引用した[ 10] シュタルク効果 による補正を導いた。ルンゲ=レンツベクトルについては、パウリは「レンツによって用いられた」とのみ述べているが、その後、物理学ではルンゲ=レンツベクトルの名で定着するに至った[ 4]
なお、ルンゲとレンツの名を冠するルンゲ=レンツベクトルだが、その発見の歴史はさらに時代を遡り、また、何度か独立に再発見されてきた[ 4] [ 9] ピエール=シモン・ラプラス 、または四元数 を発見したことで知られるアイルランドの数学者ウィリアム・ローワン・ハミルトン によるものとしている[ 4] Traité de mécanique céleste " の第1巻において、ルンゲ=レンツベクトルに相当する保存量を導いている。ラプラスは楕円軌道となる天体の運動を論じた章の中で、エネルギー、角運動量ベクトル、ルンゲ=レンツベクトルに相当する7個の第一積分 を導き、さらにこれらのうち、5個だけが独立であることを指摘している[ 7] [ 8] アイルランド王立アカデミー (英語版 ) [ 11]
ハミルトン形式の解析力学 で記述すれば、ケプラー問題の対称性とルンゲ=レンツベクトルの性質がより明らかになる。角運動量ベクトル L L 1 , L 2 , L 3 )ポアソン括弧 は
{
L
1
,
L
2
}
=
L
3
,
{
L
2
,
L
3
}
=
L
1
,
{
L
3
,
L
1
}
=
L
2
{\displaystyle \{L_{1},L_{2}\}=L_{3},\,\{L_{2},L_{3}\}=L_{1},\,\{L_{3},L_{1}\}=L_{2}}
という3次特殊直交群 SO(3) に対応する関係式を満たす。ここでエディントンのイプシロン εijk を用いれば、
{
L
i
,
L
j
}
=
∑
k
=
1
3
ϵ
i
j
k
L
k
{\displaystyle \{L_{i},L_{j}\}=\sum _{k=1}^{3}\epsilon _{ijk}L_{k}}
と表すことができる。また、角運動量ベクトルとルンゲ=レンツベクトルのポアソン括弧は
{
A
i
,
L
j
}
=
∑
k
=
1
3
ϵ
i
j
k
A
k
{\displaystyle \{A_{i},L_{j}\}=\sum _{k=1}^{3}\epsilon _{ijk}A_{k}}
となる。一方、ルンゲ=レンツベクトル同士のポアソン括弧は、例えば
{
A
1
,
A
2
}
=
−
(
p
2
−
2
m
k
r
)
L
3
=
−
2
m
E
L
3
{\displaystyle \{A_{1},A_{2}\}=-\left(p^{2}-{\frac {2mk}{r}}\right)L_{3}=-2mEL_{3}}
となり、定数項 −2mE の係数が付く。ここで E < 0
D
=
A
−
2
m
E
{\displaystyle {\boldsymbol {D}}={\frac {\boldsymbol {A}}{\sqrt {-2mE}}}}
を導入すれば、
{
L
i
,
L
j
}
=
∑
k
=
1
3
ϵ
i
j
k
L
k
{\displaystyle \{L_{i},L_{j}\}=\sum _{k=1}^{3}\epsilon _{ijk}L_{k}}
{
D
i
,
L
j
}
=
∑
k
=
1
3
ϵ
i
j
k
D
k
{\displaystyle \{D_{i},L_{j}\}=\sum _{k=1}^{3}\epsilon _{ijk}D_{k}}
{
D
i
,
D
j
}
=
∑
k
=
1
3
ϵ
i
j
k
L
k
{\displaystyle \{D_{i},D_{j}\}=\sum _{k=1}^{3}\epsilon _{ijk}L_{k}}
と簡明にまとめられる。この関係式はSO(3) を拡大したSO(4) に対応付けられる。
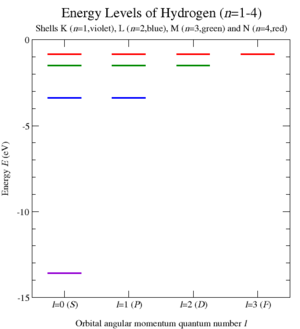
水素原子 (Z = 1n 、方位量子数 l 、磁気量子数 m で指定されるが、エネルギー準位は主量子数だけで定まり、n 2 量子力学においては、対称性は保存量と結び付き、エネルギー準位の縮退 を導く。水素型原子モデルのエネルギー固有状態 は主量子数 n 、方位量子数 l 、磁気量子数 m で指定されるが、エネルギー準位は主量子数だけで定まり、n 2 SO(3) で表される回転対称性により、角運動量が保存量となる。但し、回転対称性だけでは −l , −l + 1, …, 0, …, l − 1, l の値をとる磁気量子数による (2l + 1) 重の縮退しか説明できない。このことは、さらに別の対称性の存在を示唆する。この対称性こそが、束縛状態で角運動量とルンゲ=レンツベクトルがなすSO(4) の対称性である。
量子力学では正準量子化 により、力学的な物理量はエルミート演算子 になる。演算子(の各座標成分)同士の積は可換 とは限らず、古典力学とは違い演算子 ˆ p ˆ L −ˆ L ˆ p に一致しない[ 注 7] ˆ p ˆ L [ 注 8]
A
^
=
1
2
(
p
^
×
L
^
−
L
^
×
p
^
)
−
m
k
r
^
r
{\displaystyle {\hat {\boldsymbol {A}}}={\frac {1}{2}}({\hat {\boldsymbol {p}}}\times {\hat {\boldsymbol {L}}}-{\hat {\boldsymbol {L}}}\times {\hat {\boldsymbol {p}}})-mk{\frac {\hat {\boldsymbol {r}}}{r}}}
で定義される。
ˆ A ˆ H ハイゼンベルク方程式 からの帰結として保存量であるといえる。
i
ℏ
d
A
^
d
t
=
[
A
^
,
H
^
]
=
0
{\displaystyle i\hbar {\frac {\mathrm {d} {\hat {\boldsymbol {A}}}}{\mathrm {d} t}}=[{\hat {\boldsymbol {A}}},\,{\hat {H}}]=0}
また、古典論での関係式に類似した下記の関係を満たす。
A
^
⋅
L
^
=
L
^
⋅
A
^
=
0
{\displaystyle {\hat {\boldsymbol {A}}}\cdot {\hat {\boldsymbol {L}}}={\hat {\boldsymbol {L}}}\cdot {\hat {\boldsymbol {A}}}=0}
A
^
2
=
m
2
k
2
+
2
m
H
^
(
L
^
2
+
ℏ
2
)
{\displaystyle {\hat {\boldsymbol {A}}}^{2}=m^{2}k^{2}+2m{\hat {H}}({\hat {\boldsymbol {L}}}^{2}+\hbar ^{2})}
古典論と同様に E < 0
D
^
=
A
^
−
2
m
E
{\displaystyle {\hat {\boldsymbol {D}}}={\frac {\hat {\boldsymbol {A}}}{\sqrt {-2mE}}}}
を導入すれば、ˆ L SO(4) に対応する
[
L
^
i
,
L
^
j
]
=
i
ℏ
∑
k
=
1
3
ϵ
i
j
k
L
^
k
{\displaystyle [{\hat {L}}_{i},{\hat {L}}_{j}]=i\hbar \sum _{k=1}^{3}\epsilon _{ijk}{\hat {L}}_{k}}
[
D
^
i
,
L
^
j
]
=
i
ℏ
∑
k
=
1
3
ϵ
i
j
k
D
^
k
{\displaystyle [{\hat {D}}_{i},{\hat {L}}_{j}]=i\hbar \sum _{k=1}^{3}\epsilon _{ijk}{\hat {D}}_{k}}
[
D
^
i
,
D
^
j
]
=
i
ℏ
∑
k
=
1
3
ϵ
i
j
k
L
^
k
{\displaystyle [{\hat {D}}_{i},{\hat {D}}_{j}]=i\hbar \sum _{k=1}^{3}\epsilon _{ijk}{\hat {L}}_{k}}
が成り立つ。すなわち、SO(3) またはそれと局所同型 なSU(2) に対応していた ˆ L リー代数 は、SO(4) のものに拡張される。さらに、
I
^
=
1
2
(
L
^
+
D
^
)
{\displaystyle {\hat {\boldsymbol {I}}}={\frac {1}{2}}({\hat {\boldsymbol {L}}}+{\hat {\boldsymbol {D}}})}
K
^
=
1
2
(
L
^
−
D
^
)
{\displaystyle {\hat {\boldsymbol {K}}}={\frac {1}{2}}({\hat {\boldsymbol {L}}}-{\hat {\boldsymbol {D}}})}
を導入すると、これらは
[
I
^
i
,
I
^
j
]
=
i
ℏ
∑
k
=
1
3
ϵ
i
j
k
I
^
k
{\displaystyle [{\hat {I}}_{i},{\hat {I}}_{j}]=i\hbar \sum _{k=1}^{3}\epsilon _{ijk}{\hat {I}}_{k}}
[
K
^
i
,
K
^
j
]
=
i
ℏ
∑
k
=
1
3
ϵ
i
j
k
K
^
k
{\displaystyle [{\hat {K}}_{i},{\hat {K}}_{j}]=i\hbar \sum _{k=1}^{3}\epsilon _{ijk}{\hat {K}}_{k}}
[
I
^
i
,
K
^
j
]
=
0
{\displaystyle [{\hat {I}}_{i},{\hat {K}}_{j}]=0}
[
I
^
,
H
^
]
=
[
K
^
,
H
^
]
=
0
{\displaystyle [{\hat {\boldsymbol {I}}},{\hat {H}}]=[{\hat {\boldsymbol {K}}},{\hat {H}}]=0}
と独立な2つのSO(3) またはSU(2) に付随したリー代数をなす。したがって、角運動量演算子の場合と同様にハミルトニアンを同時対角化する ˆ I 2 , ˆ K 2
I
^
2
=
s
(
s
+
1
)
ℏ
2
s
=
0
,
1
2
,
1
,
⋯
{\displaystyle {\hat {\boldsymbol {I}}}^{2}=s(s+1)\hbar ^{2}\quad s=0,{\frac {1}{2}},1,\cdots }
K
^
2
=
s
′
(
s
′
+
1
)
ℏ
2
s
′
=
0
,
1
2
,
1
,
⋯
{\displaystyle {\hat {\boldsymbol {K}}}^{2}=s'(s'+1)\hbar ^{2}\quad s'=0,{\frac {1}{2}},1,\cdots }
となる。一方、SO(4) に付随するリー代数は階数2であり、リー代数の全ての元と可換となるカシミール演算子 (英語版 )
I
^
2
=
1
4
(
L
^
+
D
^
)
2
{\displaystyle {\hat {\boldsymbol {I}}}^{2}={\frac {1}{4}}({\hat {\boldsymbol {L}}}+{\hat {\boldsymbol {D}}})^{2}}
K
^
2
=
1
4
(
L
^
−
D
^
)
2
{\displaystyle {\hat {\boldsymbol {K}}}^{2}={\frac {1}{4}}({\hat {\boldsymbol {L}}}-{\hat {\boldsymbol {D}}})^{2}}
が該当する。
カシミール演算子としては、ˆ I 2 , ˆ K 2 線形結合 として
C
1
^
=
I
^
2
+
K
^
2
=
1
2
(
L
^
2
+
D
^
2
)
{\displaystyle {\hat {C_{1}}}={\hat {\boldsymbol {I}}}^{2}+{\hat {\boldsymbol {K}}}^{2}={\frac {1}{2}}({\hat {\boldsymbol {L}}}^{2}+{\hat {\boldsymbol {D}}}^{2})}
C
2
^
=
I
^
2
−
K
^
2
=
L
^
⋅
D
^
{\displaystyle {\hat {C_{2}}}={\hat {\boldsymbol {I}}}^{2}-{\hat {\boldsymbol {K}}}^{2}={\hat {\boldsymbol {L}}}\cdot {\hat {\boldsymbol {D}}}}
をとることができる。ここで、ˆ L ˆ D SO(4) のなすリー代数を ˆ I 2 = ˆ K 2 s = s ′ˆ C 1
C
1
^
=
2
s
(
s
+
1
)
ℏ
2
{\displaystyle {\hat {C_{1}}}=2s(s+1)\hbar ^{2}}
となる。一方、
C
1
^
=
1
2
(
L
^
2
−
1
2
m
E
A
^
2
)
=
−
m
k
2
4
E
−
1
2
ℏ
2
{\displaystyle {\hat {C_{1}}}={\frac {1}{2}}\left({\hat {\boldsymbol {L}}}^{2}-{\frac {1}{2mE}}{\hat {\boldsymbol {A}}}^{2}\right)=-{\frac {mk^{2}}{4E}}-{\frac {1}{2}}\hbar ^{2}}
であるから、水素型原子のエネルギー準位 は
E
=
−
m
k
2
2
ℏ
2
(
2
s
+
1
)
2
s
=
0
,
1
2
,
1
,
⋯
{\displaystyle E=-{\frac {mk^{2}}{2\hbar ^{2}(2s+1)^{2}}}\quad s=0,{\frac {1}{2}},1,\cdots }
となる。ここで、2s + 1 は主量子数 n に対応する。
^ より厳密に2体問題 から導出するならば、重心運動と相対運動を分離し、質点の質量 m の代わりに換算質量 、位置座標 r 相対座標 を用いればよい。
^ 原子核の周りを運動する電子が増えると遮蔽効果 が顕著となる。原子番号 Z を有効核電荷 Z eff = Z − σ σ )。
^ 特に断りのない限り、ベクトル a a と表記する。
^ ここでは Goldstein, Safko & Poole Jr. (2001) の定義に従っているが、Schiff (1968) や Greiner & Müller (1994) など他の文献では A m で割ったベクトルをルンゲ=レンツベクトルと定義している。
^ すべての束縛軌道が閉軌道となるのは、距離に反比例する中心力ポテンシャルと距離の二乗に比例する等方的な調和振動ポテンシャル のみであり、ベルトランの定理 として知られている。
^ ここでの独立とは、ハミルトン力学系のポアソン括弧 が包合系 をなすことを意味する。このとき、リウヴィルの意味で可積分 であるといわれる。
^ たとえば (ˆ p ˆ L 1 − (−ˆ L ˆ p 1
= (ˆ p 2 ˆ L 3 − ˆ p 3 ˆ L 2 ) + (ˆ L 2 ˆ p 3 − ˆ L 3 ˆ p 2 )
= [ˆ p 2 , ˆ L 3 ] − [ˆ p 3 , ˆ L 2 ]
= [ˆ p 2 , (ˆ r 1 ˆ p 2 − ˆ r 2 ˆ p 1 )] − [ˆ p 3 , (ˆ r 3 ˆ p 1 − ˆ r 1 ˆ p 3 )]
= [ˆ p 2 , −ˆ r 2 ]ˆ p 1 − [ˆ p 3 , ˆ r 3 ]ˆ p 1
= 2iħˆ p 1 ≠ 0
^ (ˆ p ˆ L † = −(ˆ L † ) × (ˆ p † ) = −ˆ L ˆ p ˆ p ˆ L






















![{\displaystyle i\hbar {\frac {\mathrm {d} {\hat {\boldsymbol {A}}}}{\mathrm {d} t}}=[{\hat {\boldsymbol {A}}},\,{\hat {H}}]=0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e49ffde7b8dab5ba331964ab5e9ed780f395dc67)



![{\displaystyle [{\hat {L}}_{i},{\hat {L}}_{j}]=i\hbar \sum _{k=1}^{3}\epsilon _{ijk}{\hat {L}}_{k}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/85b16d21c9d5cf34c20bfa399e582595c5dea4da)
![{\displaystyle [{\hat {D}}_{i},{\hat {L}}_{j}]=i\hbar \sum _{k=1}^{3}\epsilon _{ijk}{\hat {D}}_{k}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8dbe0f1b7538e510ddb35af20f4fcce840af58ac)
![{\displaystyle [{\hat {D}}_{i},{\hat {D}}_{j}]=i\hbar \sum _{k=1}^{3}\epsilon _{ijk}{\hat {L}}_{k}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/59d350be332d20d47b8d4a7559355423f5406a01)


![{\displaystyle [{\hat {I}}_{i},{\hat {I}}_{j}]=i\hbar \sum _{k=1}^{3}\epsilon _{ijk}{\hat {I}}_{k}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ebf59669a727e71e700f9d7ad86c885be9be0c6a)
![{\displaystyle [{\hat {K}}_{i},{\hat {K}}_{j}]=i\hbar \sum _{k=1}^{3}\epsilon _{ijk}{\hat {K}}_{k}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4760a83b75ea794d02e8a427153b69d1e26151ef)
![{\displaystyle [{\hat {I}}_{i},{\hat {K}}_{j}]=0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/09edbdefc1dab0fec7ed35f650be3dbf4804c2bb)
![{\displaystyle [{\hat {\boldsymbol {I}}},{\hat {H}}]=[{\hat {\boldsymbol {K}}},{\hat {H}}]=0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a2892321c2adb4701ab2bc0f44f0f45cfea052d2)








