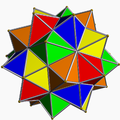
Poliedro composto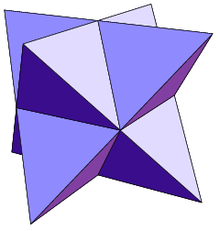

La stella ottangola è il più semplice poliedro composto regolare, ed è l'unione di due tetraedri in posizione duale.

In geometria solida si chiama poliedro composto o composto poliedrico una figura geometrica formata da due o più poliedri che condividono un baricentro comune.

Ad ogni composto poliedrico sono associate due particolari caratteristiche che individuano due nuovi poliedri ad esso correlati:

– la chiusura convessa di un composto è il più piccolo poliedro convesso che lo contiene;

– l'intersezione o nucleo di un composto è la porzione di spazio comune a tutti i suoi componenti.

Si deduce facilmente che il nucleo di un composto poliedrico è esso stesso un poliedro ed in particolare che è un poliedro convesso se tutti i componenti sono convessi.

La chiusura convessa è detta anche, in maniera del tutto equivalente, inviluppo convesso oppure involucro convesso.

Un esempio di composto poliedrico è la stella ottangola mostrata in figura: essa è un composto di due tetraedri regolari ed ha come chiusura convessa un cubo e come nucleo un ottaedro.

Composti regolari

Un composto poliedrico si dice regolare se soddisfa le normali condizioni di regolarità che valgono anche per i poliedri semplici (non composti) ossia deve essere omogeneo nei vertici, negli spigoli e nelle facce: cioè per ogni coppia di vertici (o di spigoli o di facce) esiste una simmetria del poliedro che trasforma uno dei due elementi nel secondo.

Risulta evidente perciò che affinché un composto sia regolare è necessario – ma non sufficiente – che tutti i suoi componenti siano regolari ed eguali tra loro. Più nello specifico i componenti saranno esclusivamente tetraedri, ottaedri o cubi.

Esistono in tutto 5 poliedri composti regolari (ovvero 6 se si considerano le due forme chirali di uno come due poliedri distinti). Sono elencati di seguito:

componenti	figura	elementi notevoli	inviluppo convesso	intersezione	simmetrie	duale
2 tetraedri		V = 8 S = 12 F = 8	cubo	ottaedro	48 gruppo Oh	sé stesso
5 cubi		V = 20 S = 60 F = 30	dodecaedro	triacontaedro rombico	120 gruppo Ih	5 ottaedri
5 ottaedri		V = 30 S = 60 F = 40	icosidodecaedro	icosaedro	120 gruppo Ih	5 cubi
5 tetraedri (chirale)		V = 20 S = 30 F = 20	dodecaedro	icosaedro	60 gruppo I	5 tetraedri speculari
10 tetraedri		V = 20 S = 60 F = 40	dodecaedro	icosaedro	120 gruppo Ih	sé stesso

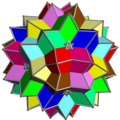
I gruppi ${\displaystyle O_{h}}$ e ${\displaystyle I_{h}}$ sono rispettivamente il gruppo di simmetria dell'ottaedro e dell'icosaedro. Il gruppo ${\displaystyle I}$ è il sottogruppo in ${\displaystyle I_{h}}$ dato dalle simmetrie che preservano l'orientazione.

Il poliedro duale del composto di cinque tetraedri è l'immagine riflessa di sé stesso; l'unione dei due forma il composto di dieci tetraedri.

Composti uniformi

Una caratteristica meno restrittiva rispetto alla regolarità è quella di uniformità, che include tutti i composti con vertici omogenei, le cui facce siano poligoni regolari. Ciò implica che i componenti debbano essere essi stessi uniformi e congruenti tra loro.

Una classificazione completa di tutti i possibili composti uniformi fu fornita da John Skilling nel 1976. L'elenco enumera 75 elementi, indicati con la sigla UC (uniform compound) seguita da un indice numerico. Vi sono inclusi i 5 composti regolari, 20 composti non banali di prismi ed antiprismi, 2 classi infinite di prismi e 4 classi infinite di antiprismi. Alcuni dei composti uniformi hanno un grado di libertà rotazionale, cioè l'inclinazione dei componenti è variabile, pur mantenendo inalterate le simmetrie del composto.

• Esempi di composti poliedrici uniformi
• 
  12 tetraedri UC₀₂ (rotazione libera)
• 
  3 cubi UC₀₈
• 
  4 ottaedri UC₁₂
• 
  20 ottaedri UC₁₃ (rotazione libera)
• 
  10 ottaedri UC₁₅ (primo tipo)
• 
  10 ottaedri UC₁₆ (secondo tipo)
• 
  2n antiprismi di basi {p/q} con q dispari UC₂₂
• 
  4 prismi triangolari UC₃₀ (chirale)
• 
  6 prismi stellati pentagonali UC₃₆ (chirale)
• 
  4 prismi esagonali UC₃₈
• 
  6 prismi decagonali UC₄₀
• 
  3 antiprismi quadrati UC₄₂
• 
  2 icosaedri UC₄₆
• 
  5 icosaedri UC₄₇
• 
  5 piccoli dodecaedri stellati UC₅₁
• 
  5 tetraedri troncati UC₅₅ (chirale)
• 
  5 cubottaedri UC₅₉
• 
  2 cubi simi (speculari) UC₆₈

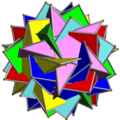
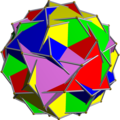
Il composto di 20 ottaedri con libertà rotazionale (UC₁₃) presenta 4 casi particolari, classificati con codici distinti: il composto regolare di 5 ottaedri (UC₁₇), due differenti composti di 10 ottaedri (UC₁₅ e UC₁₆) ed un composto di 20 ottaedri "fisso" con vertici a due a due coincidenti (UC₁₄).

I poliedri uniformi chirali (simi, camusi, retrocamusi e camusi invertiti) formano naturalmente un composto poliedrico uniforme se sovrapposti alla propria immagine riflessa. Rientra in questa categoria – pur non essendo chirale – anche l'icosaedro, considerato come un "tetraedro simo".

Non vi è alcun caso di composto poliedrico uniforme costituito da dodecaedri platonici, né da grandi dodecaedri stellati.

Bibliografia

• H. M. Cundy & A. P. Rollett, I modelli matematici, Milano, Feltrinelli, 1974.

• Maria Dedò, Forme, simmetria e topologia, Bologna, Decibel & Zanichelli, 1999, ISBN 88-08-09615-7.

• Skilling John, Uniform Compounds of Uniform Polyhedra, Mathematical Proceedings of the Cambridge Philosophical Society, 1976, DOI:10.1017/S0305004100052440.

Voci correlate

• Poliedro
• Poliedro uniforme
• Stella ottangola
• Composto di tre cubi

Altri progetti

Altri progetti

• Wikimedia Commons

• Wikimedia Commons contiene immagini o altri file su poliedro composto

Collegamenti esterni

• Modelli in carta dei poliedri, su korthalsaltes.com.
• The 75 Uniform Compounds of Uniform Polyhedra, su interocitors.com. Modelli grafici 3D di composti ad orientamento variabile.