Représentation de Hanes-Woolf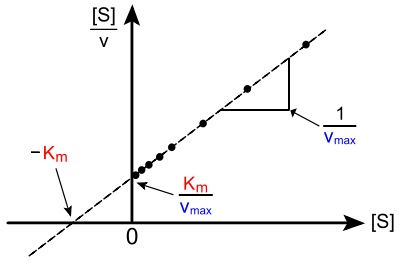

Graphique de Hanes–Woolf

En biochimie, la représentation de Hanes–Woolf est une méthode graphique utilisée en cinétique enzymatique. Elle est basée sur une version linéarisée de l'équation de Michaelis-Menten. Elle consiste à tracer le rapport [S] / v en fonction de [S], où [S] est la concentration initiale en substrat et v est la vitesse initiale de réaction.

Si la loi de vitesse suit l'équation de Michaelis-Menten, alors

${\displaystyle {[S] \over v}={[S] \over V_{\max }}+{K_{m} \over V_{\max }}}$

où K_m est la constante de Michaelis and V_max est la vitesse maximale de la réaction (à une concentration en enzyme donnée). Dans ce cas, les points expérimentaux s'alignent quand [S] / v est tracé en fonction de [S] ; la droite intersecte l'axe des abscisses à [S] = - K_M , et l'axe des ordonnées à [S] / v = K_M / V_max ; sa pente est égale à 1 / V_max.

Cette représentation est proposée par Charles Hanes en 1932[1]. Cependant, le généticien J.B.S. Haldane attribue la méthode à Barnet Woolf (en)[2].

Cette méthode, où un seul des deux axes nécessite une transformation des données, permet de limiter la propagation des erreurs de mesure. De plus, elle supporte relativement bien^[pas clair] une vaste gamme de [S]. Elle est beaucoup moins sensible que la procédure Eadie-Hofstee aux erreurs systématiques de mesure de vitesse v^[réf. nécessaire].

La plupart des spécialistes considèrent que, d'un point de vue statistique, c'est la moins mauvaise des méthodes fondées sur une transformation linéaire des données expérimentales^[réf. nécessaire].

Démonstration de l'équation

L'equation de Hanes-Wolff peut être démontrée à partir de l'équation Michaelis–Menten:

${\displaystyle v={{V_{\max }[S]} \over {K_{m}+[S]}}}$

Inverser et multiplier par [S]:

${\displaystyle {[S] \over v}={{[S](K_{m}+[S])} \over {V_{\max }[S]}}={{K_{m}+[S]} \over {V_{\max }}}}$

Réarranger:

${\displaystyle {[S] \over v}={1 \over V_{\max }}[S]+{K_{m} \over V_{\max }}}$

Notes et références

1. (en) CS Hanes, « Studies on plant amylases: The effect of starch concentration upon the velocity of hydrolysis by the amylase of germinated barley. », Biochemical Journal, vol. 26, n^o 5,‎ 1932, p. 1406–1421 (PMID 16744959, PMCID 1261052)
2. (en) J. B. S. Haldane, « Graphical Methods in Enzyme Chemistry », Nature, vol. 179, n^o 832,‎ 20 avril 1957 (DOI 10.1038/179832b0)