|
Rectangle
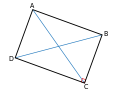
En géométrie, un rectangle est un quadrilatère dont les quatre angles sont droits. Définition et propriétésUn quadrilatère est un polygone (donc une figure plane) constitué de quatre points (appelés sommets) et de quatre segments (ou côtés) liant ces sommets deux à deux de manière à délimiter un contour fermé. Définition — Un rectangle est un quadrilatère qui possède quatre angles droits.
Démontrer qu'un quadrilatère est un rectangle Différentes propriétés caractéristiques permettent d'affirmer qu'un quadrilatère est un rectangle. Il suffit qu'un quadrilatère possède trois angles droits pour être un rectangle. Tout quadrilatère équiangle (c'est-à-dire dont les quatre angles sont égaux) est un rectangle. Si un quadrilatère est un parallélogramme, alors il est un rectangle si l'une des propriétés suivantes est vérifiée :
PropriétésUn rectangle est un cas particulier de parallélogramme, donc :
Il possède des propriétés supplémentaires :
Tout rectangle peut servir à constituer un pavage du plan. Cela signifie qu'il est possible, avec des rectangles identiques, de recouvrir tout le plan sans superposer deux rectangles. Des droites perpendiculaires partagent le plan en zones rectangulaires. Mesures
Les côtés d'un rectangle étant deux à deux de même longueur a et b, il est d'usage d'appeler dimensions du rectangle ces deux nombres. Le plus grand est la longueur du rectangle, le plus petit sa largeur. Un rectangle de côtés a et b possède une aire égale à a × b, et un périmètre de 2 × (a + b). La somme a + b est parfois appelée demi-périmètre du rectangle. L'application du théorème de Pythagore permet de constater que les diagonales du rectangle sont égales et mesurent Ces mesures sont résumées dans le tableau ci-contre. Deux rectangles qui ont même longueur a et même largeur b sont isométriques. Cela signifie qu'ils sont superposables : l'un des deux peut être transformé en l'autre par une succession de translations, rotations ou retournements. Format d'un rectangleLe quotient ab ( longueur/largeur) est appelé format du rectangle. Tous les rectangles de formats égaux sont semblables : il existe un agrandissement (ou une réduction) permettant de passer de l'un à l'autre. Autrement dit, ils ont « la même forme ». Comme la longueur est supérieure ou égale à la largeur, le format est un nombre supérieur ou égal à 1. Un format égal à 1 est caractéristique d'un carré. Plus le format est grand, plus le rectangle est « allongé ». Rectangles remarquablesCarréUn carré est un rectangle particulier dont les quatre côtés ont la même longueur. Rectangle d'orUn rectangle d'or est un rectangle dont le format est égal au nombre d'or.  Rectangles de format la racine carrée d'un entierLe rectangle de format égal à pour entier > 0 peut être construit à la règle et au compas par la méthode illustrée ci-contre. Pour , il s'agit du format A4. Pour , voir Racine_carrée_de_trois#En_géométrie. Pour , voir la particularité du billet de un dollar. Autres formats remarquablesVoir les divers formats d'écran de télévision et d'ordinateur. Une illustration de la notion de distance de HausdorffC'est ce qu'offre dans le cadre de la géométrie élémentaire le rectangle[1]:  Soit R un rectangle de largeur b et de longueur a. Alors la distance de Hausdorff entre R et sa frontière (topologie) est égale à b/2. Elle est réalisée pour tout KL où K est un point d'un segment de longueur a-b inclus dans la médiane relative à la largeur et L le projeté orthogonal de K sur une longueur du rectangle. Cette distance est utile pour calculer la distance de Hausdorff entre deux itérés successifs du tapis de Sierpinski associé à un rectangle.[réf. souhaitée]
Annexes
|
||||||||||||||||||||||||||||||||