Graphe (mathématiques discrètes)
|
Read other articles:

Panzerjäger Tiger (P) ElefantSd.Kfz. 184Un Elefant esposto all'US Army Ordnance Museum di AberdeenDescrizioneTiposemovente cacciacarri Equipaggio6 ProgettistaFerdinand Porsche CostruttoreNibelungenwerk Data impostazione22 settembre 1942 Data primo collaudo19 marzo 1943 Data entrata in servizioluglio 1943 Data ritiro dal servizio1945 Utilizzatore principale Heer Esemplari90[1] Altre variantiPanzer VI Tiger (P) Dimensioni e pesoLunghezza8,14 m[2] Larghezza3,38 m Altezza2,97 m…
2020年夏季奥林匹克运动会马来西亚代表團马来西亚国旗IOC編碼MASNOC马来西亚奥林匹克理事会網站olympic.org.my(英文)2020年夏季奥林匹克运动会(東京)2021年7月23日至8月8日(受2019冠状病毒病疫情影响推迟,但仍保留原定名称)運動員30參賽項目10个大项旗手开幕式:李梓嘉和吳柳螢(羽毛球)[1][2]閉幕式:潘德莉拉(跳水)[3]獎牌榜排名第74 金牌 銀牌 銅牌 �…

ヨハネス12世 第130代 ローマ教皇 教皇就任 955年12月16日教皇離任 964年5月14日先代 アガペトゥス2世次代 レオ8世個人情報出生 937年スポレート公国(中部イタリア)スポレート死去 964年5月14日 教皇領、ローマ原国籍 スポレート公国親 父アルベリーコ2世(スポレート公)、母アルダその他のヨハネステンプレートを表示 ヨハネス12世(Ioannes XII、937年 - 964年5月14日)は、ロー…

قوات حرس الحدود الدولة الأردن الإنشاء 2012 جزء من القوات البرية الملكية الأردنية تعديل مصدري - تعديل قيادة قوات حرس الحدود أو قوات حرس الحدود هي القوة النظامية المسؤولة عن تأمين وحماية حدود المملكة الأردنية الهاشمية والبالغ طولها 1635 كيل. حرس الحدود الأردني هي قوات من ض�…

ميت سلسيل مركز ومدينة الإحداثيات 31°10′N 31°48′E / 31.167°N 31.800°E / 31.167; 31.800 تقسيم إداري محافظة محافظة الدقهلية عاصمة لـ مركز ميت سلسيل خصائص جغرافية ارتفاع 12 متر عدد السكان (2005) المجموع 115 ألف معلومات أخرى منطقة زمنية ت ع م+02:00 (توقيت قياسي)، وت ع م+03:00 (توقي�…

South Korean actor In this Korean name, the family name is Lee. Lee Geung-youngBorn (1960-12-12) December 12, 1960 (age 63)Chungju, North Chungcheong Province, South KoreaOther namesLee Kyeong-yeong Lee Kyung-youngEducationHanyang University Theater and FilmOccupation(s)Actor, directorYears active1987–presentKorean nameHangul이경영Hanja李璟榮Revised RomanizationI Gyeong-yeongMcCune–ReischauerI Kyong-yong Lee Geung-young (born December 12, 1960) is a South Korean actor.&#…

Parish in Louisiana, United States Parish in LouisianaSt. John the Baptist ParishParishSan Francisco Plantation HouseMotto: Heart of the River ParishesLocation within the U.S. state of LouisianaLouisiana's location within the U.S.Coordinates: 30°07′N 90°30′W / 30.12°N 90.5°W / 30.12; -90.5Country United StatesState LouisianaFounded1807Named forSt. John the Baptist Catholic Church in Edgard, built 1772SeatEdgardLargest communityLaPlaceArea •&#…

Norwegian biologist Hanna Resvoll-Holmsen Hanna Marie Resvoll-Holmsen (née Resvoll) (11 September 1873 in Vågå, Oppland – 13 March 1943 in Oslo) was a Norwegian botanist – a female pioneer in Norwegian natural history education and nature conservation together with her sister, Thekla Resvoll. Life Hanna Resvoll-Holmsen suffered much from illness in her childhood and school attendance after her 12th year was sporadic. She took a high school exam in 1902, at which time she had also an unhap…

Type of nuclear reactor Aqueous homogeneous reactor at Oak Ridge National Laboratory Aqueous homogeneous reactors (AHR) is a two (2) chamber reactor consisting of an interior reactor chamber and an outside cooling and moderating jacket chamber. They are a type of nuclear reactor in which soluble nuclear salts (usually uranium sulfate or uranium nitrate) are dissolved in water. The fuel is mixed with heavy or light water which partially moderates and cools the reactor. The outside layer of the re…

Typographic symbol indicating repetition of characters above ''Ditto markIn UnicodeU+0027 ' APOSTROPHE (×2)U+0022 " QUOTATION MARKU+201D ” RIGHT DOUBLE QUOTATION MARKU+3003 〃 DITTO MARK (CJK character)Different fromDifferent fromU+2033 ″ DOUBLE PRIME The ditto mark is a shorthand sign, used mostly in hand-written text, indicating that the words or figures above it are to be repeated.[1][2] The mark is made usin…

Hanya KamuNama alternatifCoboy Jr.: Hanya KamuGenre Drama Roman Remaja PembuatStarvisionSutradaraM. HaikalPemeran Iqbaal Dhiafakhri Bastian Steel Alvaro Chance Teuku Ryzki Bella Besara Salsha Bessara Sharon Bessara Cassandra Bessara Penggubah lagu temaCoboy Junior & BeSSaRaLagu pembukaKamu oleh Coboy JuniorLagu penutupMalu Tapi Mau oleh BeSSaRaPenata musik Eka Firdaus Tya Subiakto Candil Negara asalIndonesiaBahasa asliBahasa IndonesiaJmlh. musim2Jmlh. episode59ProduksiProduser eksekuti…

Discovered among the Dead Sea Scrolls near Qumran, Israel, were fragments of a scroll which describes New Jerusalem in minute detail. The New Jerusalem Scroll appears to contain an apocalyptic vision, an eschatological vision of the city and the temple, although, being fragmented, it is hard to categorize. Written in Aramaic, the text describes a vast city, rectangular in shape, with twelve gates and encircled by a long wall. Similar descriptions appear in Revelation 21–22 (and possibly Ezekie…

Former Montreal Diocesan Theological College building Montreal Diocesan Theological College (known as Montreal Dio) is a theological seminary of the Anglican Church of Canada. It offers the Master of Divinity, Diploma in Ministry, Bachelor of Theology, and Master of Sacred Theology (S.T.M.) to candidates for ordination and other students, from Anglican, United Church, and other traditions. It also offers a distance education program, the Reading and Tutorial Course in Theology, leading to the Li…

Australian academic economist (1931–2021) For Sir Geoffrey Harcourt (died 1356) who fought at Crécy and was made a marshal by Edward III of England, see House of Harcourt. Geoff HarcourtACPortrait of Geoff Harcourt (2016)Born(1931-06-27)27 June 1931Melbourne[1]Died7 December 2021(2021-12-07) (aged 90)Sydney, New South Wales, AustraliaNationalityAustralianAcademic careerSchool ortraditionPost-Keynesian economicsInformation at IDEAS / RePEc Geoffrey Colin Harcourt AC…
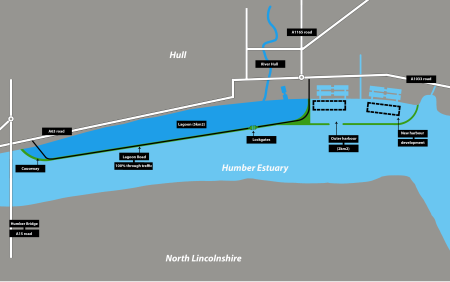
Proposed lagoon in the Humber Estuary, England Lagoon HullLooking east from the Humber Bridge, along the Yorkshire coast of the Humber EstuaryProjectCompleted2030–2035 (projected)Construction cost£1.5 billion (2020 estimate)StatusPlannedWebsiteOfficial websitePhysical featuresStreetsA63 roadLocationPlace in East Riding of Yorkshire, EnglandCoordinates: 53°43′37″N 0°22′01″W / 53.727°N 0.367°W / 53.727; -0.367CountryEnglandCountyEast Riding of YorkshireP…

Dewan FederalPetahana(dari kiri ke kanan)Walter Thurnherr (Kanselir Federal)Albert RöstiIgnazio CassisViola Amherd (Wakil Presiden)Alain Berset (Presiden)Guy ParmelinKarin Keller-SutterElisabeth Baume-SchneiderDitunjuk olehMajelis FederalMasa jabatan4 tahun, tidak ada batasan waktuPejabat perdanaUlrich OchsenbeinJonas FurrerMartin J. MunzingerHenri DrueyFriedrich Frey-HeroséWilhelm Matthias NaeffStefano FransciniDibentuk1848; 175 tahun lalu (1848)Situs webwww.admin.ch Dewan Federal (bahas…

Artikel ini sebatang kara, artinya tidak ada artikel lain yang memiliki pranala balik ke halaman ini.Bantulah menambah pranala ke artikel ini dari artikel yang berhubungan atau coba peralatan pencari pranala.Tag ini diberikan pada Januari 2023. Brachytarsomys villosa Status konservasiRentanIUCN136399 TaksonomiKelasMammaliaOrdoRodentiaSuperfamiliMuroideaFamiliNesomyidaeGenusBrachytarsomysSpesiesBrachytarsomys villosa Petter, 1962 DistribusiPersebaran Brachytarsomys villosa Brachytarsomys villosa …

Svenska cupen 1941 Svenska cupen Finalen av Svenska cupen 1941 spelades på RåsundaEvenemangsfaktaDatum13 juli–26 oktober 1941ArrangörSvFFFinalarenaRåsundaDeltagareAntal lag32StatistikMatcher31Mål183 (5,9 per match)Publik103 117 (3 326 per match)0 MästareHälsingborgs IF (1:a titeln) FinalistIK Sleipner Följande 1942 Svenska cupen 1941 var den första säsongen av Svenska cupen. Tävlingen avslutades med finalen på Råsunda i Stockholm, där Hälsingborgs IF besegrade IK…

اتخذت العديد من التقاليد الدينية موقفا بشأنالإجهاض، وهذه المواقف تمتد على نطاق واسع كما هو مبين أدناه.[1][2] البوذية نصب تذكاري بوذي يشير للإجهاض، اليابان. ليس هناك رأي بوذي واحد يتعلق بالإجهاض.[3] بعض المصادر التقليدية، بما في ذلك بعض الرموز الرهبانية البوذية، تر�…

Title in the peerage of Ireland Viscount Doneraile 2nd CreationArms of St Leger: Azure fretty argent, a chief or[1]Creation date22 June 1785CreationSecondCreated byGeorge IIIPeeragePeerage of IrelandFirst holderSt Leger St Leger, 1st Viscount DonerailePresent holderRichard St Leger, 10th Viscount DoneraileHeir apparentThe Hon. Nathaniel St LegerSubsidiary titlesBaron DoneraileMottoHAUT ET BON (French for Great and good) Viscount Doneraile 1st CreationCreation date23 June 1703CreationFirs…




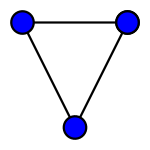






![{\displaystyle [v_{i},v_{i+1}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d3e191d44e300edb46fc9b9a1fbc9ca6f3e9da40)

![{\displaystyle [v_{n},v_{1}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b4a167d15d324cfa222111e35bd2fe5d7576e41f)

