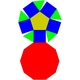
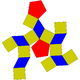
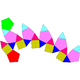
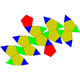
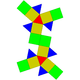
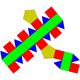
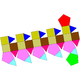
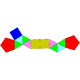
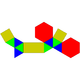
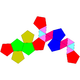
ca S%C3%B2lid de Johnson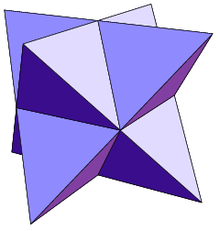

En geometria, un sòlid de Johnson és un políedre estrictament convex tal que totes les seves cares són polígons regulars però que no és ni un sòlid platònic, ni un sòlid arquimedià, ni un prisma ni un antiprisma. No cal que cada cara sigui un polígon idèntic, o que els mateixos polígons es trobin al voltant de cada vèrtex. Un exemple de sòlid de Johnson és la piràmide de base quadrada amb costats triangulars equilàters (J1); té una cara quadrada i quatre cares triangulars.

Com que és un sòlid estrictament convex pel capbaix tres cares s'han de trobar a cada vèrtex i la suma dels seus angles ha de ser menor que 360 graus. Ja que tot polígon regular té angles superiors o iguals a 60 graus (cas del triangle equilàter és 60 graus i tots els altres és més), se'n dedueix que cinc cares el màxim que es poden trobar en un vèrtex qualsevol. La piràmide pentagonal (J₂) és un exemple que té un vèrtex de grau 5.

Encara que no existeixi restricció evident perquè un polígon regular qualsevol pugui ser una cara d'un sòlid de Johnson, es troba que les cares dels sòlids de Johnson tenen sempre 3, 4, 5, 6, 8 o 10 costats. És a dir no hi ha cap sòlid de Jonson que tingui una cara que sigui un polígon ni de 7 ni de 9 ni de més de 10 costats.

El 1966, Norman Johnson va publicar una llista que incloïa els 92 sòlids, i els va donar els seus noms i els seus nombres. No va demostrar que no n'existia més que 92, però va conjecturar que no n'hi havia d'altres. Victor Zalgaller el 1969 va demostrar que la llista de Johnson era completa. S'utilitzen els noms i l'ordre donats per Johnson, i se'ls anota J_xx on xx és el nombre donat per Johnson.

Dels sòlids de Johnson, la girobicúpula quadrada allargada (J₃₇) és l'únic que és de vèrtexs uniformes: incideixen quatre cares a cada vèrtex, i el seu arranjament és sempre el mateix: tres quadrats i un triangle.

Noms

Els noms es llisten davall i són força descriptius. Molts d'aquests sòlids es poden construir afegint piràmides, cúpules i rotondes sobre cares de sòlids platònics, sòlids arquimedians, de prismes o d'antiprismes.

El prefix Bi- vol dir que s'ajunten base sobre base dues còpies del sòlid en qüestió. Per a les cúpules i les rotondes, es poden ajuntar de forma que les cares es trobin (orto-) o no (giro-). En aquesta nomenclatura, un octàedre s'anomenaria una bipiràmide quadrada, un cuboctaèdre s'anomenaria una girobicúpula hexagonal i un icosidodécaèdre una girobirotonda decagonal.

Allargat vol dir que s'ha ajuntat un prisma a la base del sòlid en qüestió o entre les bases dels sòlids en qüestió. Un rombicuboctàedre s'anomenaria una ortobicúpula octogonal allargada.
Giroallargat significa que s'ha ajuntat un antiprisma a la base del sòlid en qüestió o entre les bases dels sòlids en qüestió. Un icosàedre s'anomenaria una bipiràmide pentagonal giroallargada.

Augmentat significa que s'ha ajuntat una piràmide o una cúpula a una cara del sòlid en qüestió.
Disminuït significa que s'ha tret una piràmide o una cúpula del sòlid en qüestió.

Gir significa que una cúpula sobre el sòlid en qüestió ha sofert una rotació tal que les diferents arestes coincideixen, com per a la diferència entre orto i giro bicúpules.

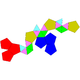
Les tres últimes operacions - augment, disminució i gir - es poden executar més d'una vegada sobre un sòlid prou gran. S'afegeix bi- al nom de l'operació per indicar que s'ha executat dues vegades. (Un sòlid bigirat té dues de les seves cúpules que han experimentat una rotació). S'afegeix tri- per indicar que s'ha executat tres vegades. (Un sòlid tridisminuit té tres de les seves piràmides o cúpules eliminades).

A vegades, bi- tot sol no és prou precís. S'ha de distingir entre un sòlid que té dues cares paral·leles alterades i un que té dues cares obliqües alterades. Quan les dues cares alterades són paral·leles, s'afegeix para- al nom de l'operació. (Un sòlid parabiaugmentat té dues cares paral·leles augmentades). Quan no ho són, s'afegeix meta- al nom de l'operació. (Un sòlid metabiaugmentat té dues cares obliqües augmentades).

Llista i noms dels políedres de Johnson

A les taules es fan servir les següents abreviatures:

V : nombre de vèrtexs,
A : nombre d'arestes,
C : nombre total de cares, on:
C₃ triangles,
C₄ quadrats,
C₅ Pentàgons,
C₆ hexàgons,
C₈ octògons,
C₁₀ decàgons.

Prismatoides i rotondes

Els poden classificar en:

J_n	Nom	V	A	C	C₃	C₄	C₅	C₆	C₈	C₁₀	Simetria

1	Piràmide quadrada	5	8	5	4	1					C_4v
2	Piràmide pentagonal	6	10	6	5		1				C_5v
3	Cúpula triangular	9	15	8	4	3		1			C_3v
4	Cúpula quadrada	12	20	10	4	5			1		C_4v
5	Cúpula pentagonal	15	25	12	5	5	1			1	C_5v
6	Rotonda pentagonal	20	35	17	10		6			1	C_5v

Piràmides modificades i bipiràmides

Es poden classificar en:

J_n	Nom	V	A	C	C₃	C₄	C₅	Simetria

7	Piràmide triangular allargada	7	12	7	4	3		C_3v
8	Piràmide quadrada allargada o (cub augmentat) o (prisma quadrat augmentat)	9	16	9	4	5		C_4v
9	Piràmide pentagonal allargada	11	20	11	5	5	1	C_5v
10	Piràmide quadrada giroallargada	9	20	13	12	1		C_4v
11	Piràmide pentagonal giroallargada o (icosàedre disminuït)	11	25	16	15		1	C_5v
12	Bipiràmide triangular	5	9	6	6			D_3h
13	Bipiràmide pentagonal	7	15	10	10			D_5h
14	Bipiràmide triangular allargada	8	15	9	6	3		D_3h
15	Bipiràmide quadrada allargada o (biaugmentat cub) o (biaugmentat prisma quadrat)	10	20	12	8	4		D_4h
16	Bipiràmide pentagonal allargada	12	25	15	10	5		D_5h
17	Bipiràmide quadrada giroallargada	10	24	16	16			D_4d

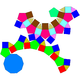
Cúpules i rotondes modificades

Es poden classificar en:

cúpules allargades
rotondes allargades
birotondes allargades
coupolo-rotondes allargades
bicúpules allargades
cúpules giroallargades
rotondes giroallargades
bicúpules
birotondes
coupulo-rotondes
bicúpules giroallargades
birotondes giroallargades
coupolo-rotondes giroallargades

J_n	Nom	V	A	C	C₃	C₄	C₅	C₆	C₈	C₁₀	Simetria

18	Cúpula triangular allargada	15	27	14	4	9		1			C_3v
19	Cúpula quadrada allargada (rombicudodecàedre disminuït)	20	36	18	4	13			1		C_4v
20	Cúpula pentagonal allargada	25	45	22	5	15	1			1	C_5v
21	Rotonda pentagonal allargada	30	55	27	10	10	6			1	C_5v
22	Cúpula triangular giroallargada	15	33	20	16	3		1			C_3v
23	Cúpula quadrada giroallargada	20	44	26	20	5			1		C_4v
24	Cúpula pentagonal giroallargada	25	55	32	25	5	1			1	C_5v
25	Rotonda pentagonal giroallargada	30	65	37	30		6			1	C_5v
26	Girobiprisma triangular	8	14	8	4	4					D_2d
27	Ortobicúpula triangular (cubooctàedre girat)	12	24	14	8	6					D_3h
28	Ortobicúpula quadrada	16	32	18	8	10					D_4h
29	Girobicúpula quadrada	16	32	18	8	10					D_4d
30	Ortobicúpula pentagonal	20	40	22	10	10	2				D_5h
31	Girobicúpula pentagonal	20	40	22	10	10	2				D_5d
32	Ortocupulorotonda pentagonal	25	50	27	15	5	7				C_5v
33	Girocupulorotonda pentagonal	25	50	27	15	5	7				C_5v
34	Ortobirotonda pentagonal (icosidodecàedre girat)	30	60	32	20		12				D_5h
35	Ortobicúpula triangular allargada	18	36	20	8	12					D_3h
36	Girobicúpula triangular allargada	18	36	20	8	12					D_3d
37	Girobicúpula quadrada allargada (rombicudodecàedre girat)	24	48	26	8	18					D_4d
38	Ortobicúpula pentagonal allargada	30	60	32	10	20	2				D_5h
39	Girobicúplula pentagonal allargada	30	60	32	10	20	2				D_5d
40	Ortocúpulorotonda pentagonal allargada	35	70	37	15	15	7				C_5v
41	Girocúpulorotonda pentagonal allargada	35	70	37	15	15	7				C_5v
42	Ortobirotonda pentagonal allargada	40	80	42	20	10	12				D_5h
43	Girobirotonda pentagonal allargada	40	80	42	20	10	12				D_5d
44	Bicúpula triangular giroallargada (2 formes quirals)	18	42	26	20	6					D₃
45	Bicúpula quadrada giroallargada (2 formes quirals)	24	56	34	24	10					D₄
46	Bicúpula pentagonal giroallargada (2 formes quirals)	30	70	42	30	10	2				D₅
47	Cúpulorotonda pentagonal giroallargada (2 formes quirals)	35	80	47	35	5	7				C₅
48	Birotonda pentagonal giroallargada (2 formes quirals)	40	90	52	40		12				D₅

Prismes augmentats

J_n	Nom	V	A	C	C₃	C₄	C₅	C₆	Symmetry

49	Prisma triangular augmentat	7	13	8	6	2			C_2v
50	Prisma triangular biaugmentat	8	17	11	10	1			C_2v
51	Prisma triangular triaugmentat	9	21	14	14				D_3h
52	Prisma pentagonal augmentat	11	19	10	4	4	2		C_2v
53	Prisma pentagonal biaugmantat	12	23	13	8	3	2		C_2v
54	Prisma hexagonal augmentat	13	22	11	4	5		2	C_2v
55	Prisma hexagonal parabiaugmentat	14	26	14	8	4		2	D_2h
56	Prisma hexagonal metabiaugmantat	14	26	14	8	4		2	C_2v
57	Prisma hexagonal triaugmentat	15	30	17	12	3		2	D_3h

Sòlids platònics modificats

Dodecàedres augmentats
Icosàedres disminuïts

J_n	Nom	V	A	C	C₃	C₅	Simetria

58	Dodecàedre augmentat	21	35	16	5	11	C_5v
59	Dodecàedre parabiaugmentat	22	40	20	10	10	D_5d
60	Dodecàedre metabiaugmentat	22	40	20	10	10	C_2v
61	Dodecàedre triaugmentat	23	45	24	15	9	C_3v
62	Icosàedre metabidismminuït	10	20	12	10	2	C_2v
63	Icosàedre tridisminuït	9	15	8	5	3	C_3v
64	Icosàedre tridisminuït augmentat	10	18	10	7	3	C_3v

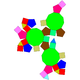
Sòlids arquimedians modificats

S'obtenen a partir de:

Tetràedre truncat (augmentat)
Cub truncat (augmentat)
Dodecàedre truncat (augmentat)
Petit romboicosidodecàedre (girat)
Petit romboicosidodecàedre (disminuït)
Petit romboicosidodecàedre (disminuït i girat)

J_n	Nom	V	A	C	C₃	C₄	C₅	C₆	C₈	C₁₀	Simetria

65	Tetràedre truncat augmentat	15	27	14	8	3		3			C_3v
66	Cub truncat augmentat	28	48	22	12	5			5		C_4v
67	Cub truncat biaugmentat	32	60	30	16	10			4		D_4h
68	Dodecàedre truncat augmentat	65	105	42	25	5	1			11	C_5v
69	Dodecàedre truncat parabiaugmentat	70	120	52	30	10	2			10	D_5d
70	Dodecàedre truncat metabiaugmentat	70	120	52	30	10	2			10	C_2v
71	Dodecàedre truncat triaugmentat	75	135	62	35	15	3			9	C_3v
72	Romboicosidodecàedre girat	60	120	62	20	30	12				C_5v
73	Romboicosidodecàedre parabigirat	60	120	62	20	30	12				D_5d
74	Romboicosidodecàedre metabigirat	60	120	62	20	30	12				C_2v
75	Romboicosidodecàedre Trigirat	60	120	62	20	30	12				C_3v
76	Romboicosidodecàedre disminuït	55	105	52	15	25	11			1	C_5v
77	Romboicosidodecàedre disminuït paragirat	55	105	52	15	25	11			1	C_5v
78	Romboicosidodecàedre disminuït metagirat	55	105	52	15	25	11			1	C_s
79	Romboicosidodecàedre disminuït bigyiat	55	105	52	15	25	11			1	C_s
80	Romboicosidodecàedre parabidisminuït	50	90	42	10	20	10			2	D_5d
81	Romboicosidodecàedre metabidisminuït	50	90	42	10	20	10			2	C_2v
82	Romboicosidodecàedre bidisminuït girat	50	90	42	10	20	10			2	C_s
83	Romboicosidodecàedre tridisminuït	45	75	32	5	15	9			3	C_3v

Diversos

J_n	Nom	V	A	C	C₃	C₄	C₅	C₆	Simetria

84	Bisfenoide xato (Dodecàedre siamès)	8	18	12	12				D_2d
85	Atiprisma quadrat xato	16	40	26	24	2			D_4d
86	Esfenocorona	10	22	14	12	2			C_2v
87	Esfenocorona augmentada	11	26	17	16	1			C_s
88	Esfenomegacorona	12	28	18	16	2			C_2v
89	Hebesfenomegacorona	14	33	21	18	3			C_2v
90	Disfenocíngol	16	38	24	20	4			D_2d
91	Birotonda billunar	14	26	14	8	2	4		D_2h
92	Hebesfenorotonda triangular	18	36	20	13	3	3	1	C_3v

Referències

Norman W. Johnson, "Convex Solids with Regular Faces", Canadian Journal of Mathematics, 18, 1966, pages 169–200. Conté l'enumeració original dels 92 sòlids i la conjectura que no n'hi ha d'altres.
Victor A. Zalgaller, "Convex Polyhedra with Regular Faces", 1969 : primera demostració d'aquesta conjectura.
Eric W. Weisstein. Johnson Solid : cada sòlid amb el seu desenvolupament

Enllaços externs

A Wikimedia Commons hi ha contingut multimèdia relatiu a: Sòlid de Johnson

(anglès) Paper Models of Polyhedra
(anglès) Sòlids de Johnson per George W. Hart.
(anglès) Imatges dels 92 sòlids, categoritzats, en una pàgina. Arxivat 2013-06-01 a Wayback Machine.

Sòlid de Johnson