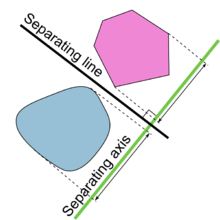
超平面分离定理(英語:hyperplane separation theorem)是几何学中关于n维欧几里德空间中不相交凸集的定理,有几个相当相似的版本。在该定理的一种版本中,如果这两个集合都是闭集并且至少其中一个是紧的,那么它们之间存在一个超平面,甚至它们之间存在两个由间隙隔开的平行超平面。 在另一个版本中,如果两个不相交的凸集都是开集,那么它们之间有一个超平面,但不一定有任何间隙。 与分离超平面正交的轴是分离轴,因为凸体在该轴上的正交投影是不相交的[1]。
超平面分离定理由赫尔曼·闵可夫斯基提出,後哈恩-巴纳赫分离定理将结果推广到拓扑向量空间。在支持向量机的背景下,最佳分离超平面或最大边缘超平面是分离两个点凸包并且与两者等距的超平面[2][3]。
参考资料
- ^ Witten, Ian H.; Frank, Eibe; Hall, Mark A.; Pal, Christopher J. Data Mining: Practical Machine Learning Tools and Techniques Fourth. Morgan Kaufmann. 2016: 253–254. ISBN 9780128043578.
- ^ Hastie, Trevor; Tibshirani, Robert; Friedman, Jerome. The Elements of Statistical Learning : Data Mining, Inference, and Prediction (PDF) Second. New York: Springer. 2008: 129–135 [2023-10-09]. (原始内容存档 (PDF)于2018-09-28).
- ^ Deisenroth, Marc Peter; Faisal, A. Aldo; Ong, Cheng Soon. Mathematics for Machine Learning. Cambridge University Press. 2020: 337–338. ISBN 978-1-108-45514-5.