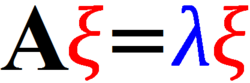特征值和特征向量

「特征向量」和「特征空间」均重定向至此。关于机器学习中的概念，请见「特徵 (机器学习)」。

线性代数
${\displaystyle \mathbf {A} ={\begin{bmatrix}1&2\\3&4\end{bmatrix}}}$
向量 · 向量空间 · 基底  · 行列式  · 矩阵
向量 标量 · 向量 · 向量空间 · 向量投影 · 外积（向量积 · 七维向量积） · 内积（数量积） · 二重向量 矩阵与行列式 矩阵 · 行列式 · 线性方程组 · 秩 · 核 · 跡 · 單位矩陣 · 初等矩阵 · 方块矩阵 · 分块矩阵 · 三角矩阵 · 非奇异方阵 · 转置矩阵 · 逆矩阵 · 对角矩阵 · 可对角化矩阵 · 对称矩阵 · 反對稱矩陣 · 正交矩阵 · 幺正矩阵 · 埃尔米特矩阵 · 反埃尔米特矩阵 · 正规矩阵 · 伴随矩阵 · 余因子矩阵 · 共轭转置 · 正定矩阵 · 幂零矩阵 · 矩阵分解 （LU分解 · 奇异值分解 · QR分解 · 极分解 · 特征分解） · 子式和余子式 · 拉普拉斯展開 · 克罗内克积 线性空间与线性变换 线性空间 · 线性变换 · 线性子空间 · 线性生成空间 · 基 · 线性映射 · 线性投影 · 線性無關 · 线性组合 · 线性泛函 · 行空间与列空间 · 对偶空间 · 正交 · 特征向量 · 最小二乘法 · 格拉姆-施密特正交化
查 论 编

特征值与特征向量。在${\displaystyle A}$变换的作用下，向量${\displaystyle \xi }$仅仅在尺度上变为原来的${\displaystyle \lambda }$倍。称${\displaystyle \xi }$是A的一个特征向量，${\displaystyle \lambda }$是对应的特征值。

图1.当蒙娜丽莎的图像左右翻转时，中间垂直的红色向量方向保持不变。而水平方向上黄色的向量的方向完全反转，因此它们都是左右翻转变换的特征向量。红色向量长度不变，其特征值为1。黄色向量长度也不变但方向变了，其特征值为-1。橙色向量在翻转后和原来的向量不在同一条直线上，因此不是特征向量。

在数学上，特别是线性代数中，对于一个给定的方阵${\displaystyle A}$，它的特征向量（eigenvector，也譯固有向量、本征向量）${\displaystyle v}$ 经过这个线性变换[a]之后，得到的新向量仍然与原来的${\displaystyle v}$ 保持在同一條直線上，但其长度或方向也许會改变。即${\displaystyle Av=\lambda v}$， ${\displaystyle \lambda }$為純量，即特征向量的长度在该线性变换下缩放的比例，称${\displaystyle \lambda }$ 为其特征值（eigenvalue，也譯固有值、本征值）。如果特徵值為正，则表示${\displaystyle v}$ 在经过线性变换的作用后方向也不变；如果特徵值為負，说明方向会反转；如果特征值为0，则是表示缩回零点。但无论怎样，仍在同一条直线上。图1给出了一个以油画《蒙娜丽莎》为题材的例子。在一定条件下（如其矩阵形式为实对称矩阵的线性变换），一个变换可以由其特征值和特征向量完全表述，也就是說：所有的特徵向量組成了這向量空間的一組基底。一个特征空间（eigenspace）是具有相同特征值的特征向量与一个同维数的零向量的集合，可以证明该集合是一个线性子空间，比如${\displaystyle \textstyle E_{\lambda }=\{u\in V\mid Au=\lambda u\}}$ 即為線性變換${\displaystyle A}$ 中以${\displaystyle \lambda }$ 為特徵值的特徵空間。

这些概念在纯数学和应用数学的众多领域中都有重要的应用。在线性代数和泛函分析之外，甚至在一些非线性的情况下，这些概念都是十分重要的。

「特征」一詞譯自德语的eigen，由希尔伯特在1904年首先在这个意义下使用（赫尔曼·冯·亥姆霍兹在更早的时候也在类似意义下使用过这一概念）。eigen一詞可翻译为“自身的”，“特定于...的”，“有特征的”或者“个体的”—这强调了特征值对于定义特定的变换上是很重要的。

定义

图解特征向量

给定一个向量空间${\displaystyle \mathbf {E} }$，从${\displaystyle \mathbf {E} }$到${\displaystyle \mathbf {E} }$自身的线性变换${\displaystyle \mathbf {T} }$是一个保持向量加法和純量乘向量這兩種運算的函数，例如旋转、反射、拉伸、压缩，或者这些变换的组合等等[1]。一个线性变换可以通过它们在向量上的作用来可视化。一般来说，一个向量在经过映射之后可以变为任何可能的向量，而特征向量具有更好的性质[2]。

一个线性变换${\displaystyle \mathbf {T} :\mathbf {E} \mapsto \mathbf {E} }$的特征向量${\displaystyle v}$ 是一個非零向量[b]且在这个线性变换下的新向量為${\displaystyle v}$ 简单地乘以一个标量${\displaystyle \lambda }$[2]。也就是说存在一個純量${\displaystyle \lambda }$　使得${\displaystyle v}$满足下式：

${\displaystyle \mathbf {T} (v)=\lambda v}$

其中的缩放因子${\displaystyle \lambda }$ 称为这个特征向量的特征值，或者说是线性变换${\displaystyle \mathbf {T} }$的特征值。反过来，一个实数${\displaystyle \lambda }$是线性变换${\displaystyle \mathbf {T} }$的一个特征值，当且仅当有一个非零向量${\displaystyle v}$满足上面的式子[2][3]。

所有具有相同的特征值${\displaystyle \lambda }$的特征向量和零向量一起，组成了一个向量空间，称为线性变换的一个特征空间，一般记作${\displaystyle \mathbb {E} _{\lambda }(\mathbf {T} )}$[4]。这个特征空间如果是有限维的，那么它的维数叫做${\displaystyle \lambda }$的几何重数[5]。

变换的主特征向量是模最大的特征值对应的特征向量[6]。有限维向量空间上的一个变换的谱是其所有特征值的集合[7]。

特征向量也可以看作是关于系数${\displaystyle \lambda }$的方程：

${\displaystyle \mathbf {T} (x)=\lambda x}$

的非零解。显然只有在${\displaystyle \lambda }$是变换${\displaystyle \mathbf {T} }$的特征值之时，方程才有非零解[8]。

例子

线性变换

最简单的例子是恒等变换${\displaystyle \mathbf {I} }$的特征向量。由于对所有的非零向量${\displaystyle v}$，

${\displaystyle \mathbf {I} (v)=v=1\cdot v}$

所以所有的非零向量都是恒等变换${\displaystyle \mathbf {I} }$的特征向量，对应着特征值1。恒等变换的特征空间只有一个，就是整个空间，对应着特征值1。[9]类似地，数乘变换${\displaystyle \lambda \mathbf {I} }$的特征向量也是所有非零向量，因为按照定义，对所有的非零向量${\displaystyle v}$，

${\displaystyle \lambda \mathbf {I} (v)=\lambda \cdot v}$

如果一个变换可以写成对角矩阵，那么它的特征值就是它对角线上的元素，而特征向量就是相应的基。例如矩阵：

${\displaystyle \mathbf {A} ={\begin{bmatrix}2&0&0\\0&2&0\\0&0&4\end{bmatrix}}}$

的特征值就是2和4。2对应的特征向量是所有形同${\displaystyle (a,b,0)^{T}}$的非零向量，而4对应的特征向量是所有形同${\displaystyle (0,0,c)^{T}}$的非零向量。2对应的特征空间是一个2维空间，而4对应的特征空间是一个1维空间。矩阵${\displaystyle \mathbf {A} }$的谱是${\displaystyle \left\{2,4\right\}}$。

在这个错切变换中，蒙娜丽莎的图像被变形，但是垂直的红色向量在变换下保持不变，而蓝色的向量，从胸部到肩膀，其方向改变了。因此红色向量是该变换的一个特征向量，而蓝色的不是。红色向量长度不变，特征值为1。所有沿着垂直线的向量也都是特征向量，它们的特征值相等。它们构成这个特征值的特征空间。

对于更复杂的矩阵，特征向量和特征值就不是显然的了。右图中的例子是一个二维平面上的错切变换，其矩阵可以表示为：

${\displaystyle \mathbf {A} ={\begin{bmatrix}1&0\\-{\frac {1}{2}}&1\end{bmatrix}}}$

${\displaystyle \mathbf {A} }$的特征向量${\displaystyle \mathbf {x} }$，按照定义，是在变换${\displaystyle \mathbf {A} }$的作用下会得到${\displaystyle \mathbf {x} }$自身的若干倍的非零向量。假设在${\displaystyle \mathbf {A} }$的作用下${\displaystyle \mathbf {x} }$变成了自身的${\displaystyle \lambda }$倍，也就是

${\displaystyle \mathbf {A} \mathbf {x} =\lambda \mathbf {x} }$

在等式两边的左侧乘以单位矩阵I，得到

${\displaystyle \mathbf {IA} \mathbf {x} =\mathbf {I} \cdot \lambda \mathbf {x} }$

${\displaystyle \mathbf {A} \mathbf {x} =(\lambda I)\mathbf {x} }$

因此

${\displaystyle (\mathbf {A} -\lambda \mathbf {I} )\mathbf {x} =0}$

根据线性方程组理论，为了使这个方程有非零解，矩阵${\displaystyle \mathbf {A} -\lambda \mathbf {I} }$的行列式必须是零：

${\displaystyle \det(\mathbf {A} -\lambda \mathbf {I} )=0}$

det: determinant，行列式

按照行列式的展开定义，上面式子的左端是一个关于${\displaystyle \lambda }$的多项式，称为特征多项式。这个多项式的系数只和${\displaystyle \mathbf {A} }$有关。在这个例子中，可以计算这个特征多项式：

${\displaystyle \det \!\left({\begin{bmatrix}1&0\\-{\frac {1}{2}}&1\end{bmatrix}}-\lambda {\begin{bmatrix}1&0\\0&1\end{bmatrix}}\right)=(1-\lambda )^{2}}$

在这种情况下特征多项式的方程变成${\displaystyle (1-\lambda )^{2}=0}$。它的唯一的解是：${\displaystyle \lambda =1}$。这就是矩阵${\displaystyle \mathbf {A} }$的特征值。

找到特征值${\displaystyle \lambda =1}$后，就可以找出

${\displaystyle (\mathbf {A} -\lambda \mathbf {I} )\mathbf {x} =0}$

的非零解，也就是特征向量了。在例子中：

${\displaystyle {\begin{bmatrix}1-\lambda &0\\-{\frac {1}{2}}&1-\lambda \end{bmatrix}}{\begin{bmatrix}x_{1}\\x_{2}\end{bmatrix}}=0}$

将${\displaystyle \lambda =1}$代入，就有

${\displaystyle {\begin{bmatrix}0&0\\-{\frac {1}{2}}&0\end{bmatrix}}{\begin{bmatrix}x_{1}\\x_{2}\end{bmatrix}}=0}$

解这个新矩阵方程，得到如下形式的解：

${\displaystyle \mathbf {x} ={\begin{bmatrix}0\\c\end{bmatrix}}}$

这里的c是任意非零常量。因此，矩阵${\displaystyle \mathbf {A} }$的特征向量就是所有竖直方向的向量（比如图中红色箭头代表的向量）。

一般来说，2×2的非奇异矩阵如果有两个相异的特征值，就有两个线性无关的特征向量。在这种情况下，对于特征向量，线性变换仅仅改变它们的长度，而不改变它们的方向（除了反转以外），而对于其它向量，长度和方向都可能被矩阵所改变。如果特征值的模大于1，特征向量的长度将被拉伸，而如果特征值的模小于1，特征向量的长度就将被压缩。如果特征值小于0，特征向量将会被翻转。

其他例子

随着地球的自转，每个从地心往外指的箭头都在旋转，除了在转轴上的那些箭头。考虑地球在一小时自转后的变换：地心指向地理南极的箭头是这个变换的一个特征向量，并且因为指向极点的箭头没有被地球的自转拉伸，它的特征值是1;但是从地心指向赤道任何一处的箭头不会是一个特征向量。

另一个例子是，薄金属板关于一个固定点均匀伸展，使得板上每一个点到该固定点的距离翻倍。这个伸展是一个有特征值2的变换。从该固定点到板上任何一点的向量是一个特征向量，而相应的特征空间是所有这些向量的集合。

图2.一个两端固定的绳子上的驻波可以视为特征向量的一个例子，更精确的讲，它是一个相对于时间流逝的变换的特征函数。随着时间流逝，驻波被缩放，但是它的形状不变。在这个例子中，特征值是依赖于时间的。

但是，三维几何空间不是唯一的向量空间。例如，考虑两端固定的拉紧的绳子，就像弦乐器的振动弦那样（图2.）。振动弦的原子到它们在弦静止时的位置之间的带符号那些距离视为一个空间中的一个向量的分量，那个空间的维数就是弦上原子的个数。

如果考虑绳子随着时间流逝发生的变换，它的特征向量，或者说特征函数（如果将绳子假设为一个连续媒介），就是它的驻波—也就是那些通过空气的传播让人们听到弓弦和吉他的拨动声的振动。驻波对应于弦的特定振动，它们使得弦的形状随着时间变化而伸缩一个因子（特征值）。和弦相关的该向量的每个分量乘上了一个依赖于时间的因子。驻波的振幅（特征值）在考虑到阻尼的情况下逐渐减弱。因此可以将每个特征向量对应于一个寿命，并将特征向量的概念和共振的概念联系起来。

特征值方程

从数学上看，如果非零向量v与变换${\displaystyle {\mathcal {T}}}$满足

${\displaystyle {\mathcal {T}}(\mathbf {v} )=\lambda \,\mathbf {v} }$

则称向量v是变换${\displaystyle {\mathcal {T}}(\cdot )}$的一个特征向量，λ是相应的特征值。其中${\displaystyle {\mathcal {T}}(\mathbf {v} )}$是将变换${\displaystyle {\mathcal {T}}(\cdot )}$作用于v得到的向量。

假设${\displaystyle {\mathcal {T}}(\cdot )}$是一个线性变换，那么v可以由其所在向量空间的一组基表示为：

${\displaystyle \mathbf {v} =\sum _{i=1}^{n}v_{i}\mathbf {e} _{i}}$

其中${\displaystyle v_{i}}$是向量${\displaystyle \mathbf {v} }$在基向量${\displaystyle \mathbf {e} _{i}}$上的投影（即坐标），这里假设向量空间为n 维。由此，${\displaystyle \mathbf {v} }$可以直接以坐标向量${\displaystyle v=(v_{1},\ldots ,v_{n})^{T}}$表示。利用基向量，线性变换${\displaystyle {\mathcal {T}}(\cdot )}$也可以用一个简单的矩阵乘法表示。上述的特征值方程可以表示为：

${\displaystyle T\,v=\lambda \,v}$

但是，有时候用矩阵形式写下特征值方程是不自然甚或不可能的。例如在向量空间是无穷维的时候，上述的弦的情况就是一例。取决于变换${\displaystyle {\mathcal {T}}}$和它所作用的空间的性质，有时将特征值方程表示为一组微分方程更好。若${\displaystyle {\mathcal {T}}}$是一个微分算子，其特征向量通常称为该微分算子的特征函数。例如，微分本身是一个线性变换因为（若M和N是可微函数，而a和b是常数）

${\displaystyle {\frac {d}{dt}}(aM+bN)=a{\frac {dM}{dt}}+b{\frac {dN}{dt}}}$

考虑对于时间${\displaystyle t}$的微分。其特征函数满足如下特征值方程：

${\displaystyle {\frac {dN}{dt}}=\lambda N}$,

其中λ是该函数所对应的特征值。这样一个时间的函数，如果${\displaystyle \lambda =0}$，它就不变，如果${\displaystyle \lambda }$为正，它就按比例增长，如果${\displaystyle \lambda }$是负的，它就按比例衰减。例如，理想化的兔子的总数在兔子更多的地方繁殖更快，从而满足一个正λ的特征值方程。

该特征值方程的解是${\displaystyle N=\exp(\lambda t)}$，也即指数函数；这样，该函数是微分算子d/dt的特征值为λ的特征函数。若λ是一个负数，我们称N的演变为一个指数衰减；若它是正数，则称指数增长。λ的值可以是一个任意复数。因此d/dt的谱是整个复平面。在这个例子中，算子d/dt作用的空间是单变量可微函数的空间。该空间有无穷维（因为不是每一个可微函数都可以用有限的基函数的线性组合来表达的）。但是，每个特征值λ所对应的特征空间是一维的。它就是所有形为${\displaystyle N=N_{0}\exp(\lambda t)}$的函数的集合。N₀是任意常数，也就在t=0的初始数量。

谱定理

更多信息：谱定理

谱定理在有限维的情况，将所有可对角化的矩阵作了分类：它显示一个矩阵是可对角化的，当且仅当它是一个正规矩阵。注意这包括自共轭（厄尔米特）的情况。这很有用，因为对角化矩阵T的函数f(T)（譬如博雷尔函数f）的概念是清楚的。在采用更一般的矩阵的函数的时候谱定理的作用就更明显了。例如，若f是解析的，则它的形式幂级数，若用T取代x，可以看作在矩阵的巴拿赫空间中绝对收敛。谱定理也允许方便地定义正算子的唯一的平方根。

谱定理可以推广到希尔伯特空间上的有界正规算子，或者无界自共轭算子的情况。

矩阵的特征值和特征向量

计算矩阵的特征值和特征向量

假设我们想要计算给定矩阵的特征值。若矩阵很小，我们可以用特征多项式进行符号演算。但是，对于大型矩阵这通常是不可行的，在那种情况我们必须采用数值方法。

形式计算

更多信息：矩阵特征值的符号演算

描述正方形矩阵的特征值的重要工具是特征多项式：就如之前的例子一样，说λ是A的特征值等价于说线性系统（A – λI）v = 0（其中I是单位矩阵）有非零解v（一个特征向量），因此等价于说行列式：

${\displaystyle \det(A-\lambda I)=0\!\ }$

函数：${\displaystyle p_{A}(\lambda )=\det(A-\lambda I)\!\ }$是一个关于λ的多项式，称为A的特征多项式。矩阵的特征值也就是其特征多项式的零点。求一个矩阵A的特征值可以通过求解方程${\displaystyle p_{A}(\lambda )=0}$来得到。

若A是一个n×n矩阵，则${\displaystyle p_{A}}$为n次多项式，因而A最多有n个特征值。反过来，如果A的系数是在一个代数闭域里面（比如说复数域），那么代数基本定理说明这个方程刚好有n个根（如果重根也计算在内的话）。所有奇数次的多项式必有一个实数根，因此当n为奇数的时候，每个n维实系数矩阵至少有一个实数特征值。当矩阵系数是实数的时候，非实数的特征值会成共轭对出现。

一旦找到特征值λ，相应的特征向量就可以通过求解如下方程得到：

${\displaystyle (A-\lambda I)v=0\!\ }$

实系数的矩阵不一定有实数特征值。比如对于以下的矩阵（表示二维平面上的顺时针90°的一个旋转变换)：

${\displaystyle {\begin{bmatrix}0&1\\-1&0\end{bmatrix}}}$

其特征多项式是${\displaystyle \lambda ^{2}+1}$，因此其特征值成复共轭对出现，分别是i和-i，而没有实数特征值。相应的特征向量也是非实数的。

数值计算

更多信息：特征值算法

在实践中，大型矩阵的特征值无法通过特征多项式计算。计算该多项式本身相当费资源，而根的精确表达式对于高次的多项式来说很难计算和表达：阿貝爾-魯菲尼定理显示五次或更高次的多项式的根无法用${\displaystyle n}$次方根来简单表达。对于估算多项式的根的有效算法是有的，但特征值中的微小误差可以导致特征向量的巨大误差。因此，寻找特征多项式和特征值的一般算法，是迭代法。最简单的方法是幂法（英语：Power_method）：取一个随机向量${\displaystyle v}$，然后计算如下的一系列单位向量

${\displaystyle {\frac {Av}{||Av||}}}$, ${\displaystyle {\frac {A^{2}v}{||A^{2}v||}}}$, ${\displaystyle {\frac {A^{3}v}{||A^{3}v||}}}$, ...

这个序列几乎总是收敛于最大绝对值的特征值所对应的特征向量。这个算法很简单，但是本身不是很有用。但是，像QR分解这样的算法正是以此为基础的[10]。

性质

代数重次

A的一个特征值λ的代数重数是λ作为A的特征多项式的根的次数；换句话说，若r是该多项式的一个根，它是一次多项式因子（λ - r）在特征多项式中在因式分解后中出现的次数。如果将代数重次计算在内的话，一个n×n矩阵有n个特征值，因为其特征多项式次数为n。

一个代数重次1的特征值为“单特征值”。

在关于矩阵理论的条目中，可能会遇到如下的表示方法：

"一个矩阵A的特征值为4,4,3,3,3,2,2,1,"

表示4的代数重次为二，3的是三，2的是二，而1的是1。这样写是因为代数重次对于矩阵理论中的很多證明很重要而被大量使用。

和代数重数相对的是特征值的几何重数：特征值相对应的特征空间（也就是λI − A的零空间）的维数。代数重次也可以视为一种维数：它是相应广义特征空间的维数，也就是当自然数k足够大的时候矩阵（λI − A）^k的零空间。也就是说，它是所有“广义特征向量”组成的空间，其中一个广义特征向量是任何一个如果λI − A作用连续作用足够多次就“最终”会变0的向量。任何特征向量都是一个广义特征向量，以此任一个特征空间都被包含于相应的广义特征空间。这给了一个几何重次总是小于或等于代数重次的简单证明。

例如：

${\displaystyle A={\begin{bmatrix}1&1\\0&1\end{bmatrix}}}$。

它只有一个特征值，也就是λ = 1。其特征多项式是${\displaystyle (\lambda -1)^{2}}$，所以这个特征值代数重次为2。但是，相应特征空间是通常称为x轴的数轴，由向量${\displaystyle {\begin{bmatrix}1\\0\end{bmatrix}}}$线性生成，所以几何重次只是1。

广义特征向量可以用于计算一个矩阵的若尔当标准型（参看下面的讨论）。若尔当块通常不是对角化而是幂零的这个事实与特征向量和广义特征向量之间的区别直接相关。

一般矩阵分解定理

如上所述，谱定理表明正方形矩阵可以对角化当且仅当它是正规的。对于更一般的未必正规的矩阵，我们有类似的结果。当然在一般的情况，有些要求必须放松，例如酉等价性或者最终的矩阵的对角性。所有这些结果在一定程度上利用了特征值和特征向量。下面列出了一些这样的结果：

• 舒尔三角形式表明任何矩阵酉等价于一个上三角矩阵；
• 奇异值分解, ${\displaystyle A=U\Sigma V^{*}}$其中${\displaystyle \Sigma }$为对角阵，而U,V为酉矩阵。${\displaystyle \Sigma =U^{*}AV}$的对角线上的元素非负，而正的项称为A的奇异值。这对非正方形矩阵也成立；
• 若尔当标准型，其中${\displaystyle A=U\Lambda U^{-1}}$其中${\displaystyle \Lambda }$不是对角阵，但是分块对角阵，而${\displaystyle U}$是酉矩阵。若尔当块的大小和个数由特征值的几何和代数重次决定。若尔当分解是一个基本的结果。从它可以立即得到一个正方形矩阵可以完全用它的特征值包括重次来表述，最多只会相差一个酉等价。这表示数学上特征值在矩阵的研究中有着极端重要的作用。
• 作为若尔当分解的直接结果，一个矩阵A可以“唯一”地写作A = S + N其中S可以对角化，N是幂零的（也即，对于某个q，N^q=0），而S和N可交换（SN=NS）。
• 任何可逆矩阵A可以唯一地写作A = SJ，其中S可对角化而J是么幂矩阵（也即，使得特征多项式是(λ-1)的幂，而S和J可交换）。

特征值的一些另外的属性

谱在相似变换下不变：矩阵A和P^-1AP有相同的特征值，这对任何矩阵A和任何可逆矩阵P都成立。谱在转置之下也不变：矩阵A和A^T有相同的特征值。

因为有限维空间上的线性变换是双射当且仅当它是单射，一个矩阵可逆当且仅当所有特征值都不是0。

若尔当分解的一些更多的结果如下：

• 一个矩阵是對角矩陣当且仅当代数和几何重次对于所有特征值都相等。特别的有，一个n×n矩阵如果有n不同特征值，则总是可以对角化的。
• 矩阵作用的向量空间可以视为其广义特征向量所撑成的不变子空间的直和。对角线上的每个块对应于该直和的一个子空间。若一个块是对角化的，其不变子空间是一个特征空间。否则它是一个广义特征空间，如上面所定义；
• 因为跡，也就是矩阵主对角线元素之和，在酉等价下不变，若尔当标准型说明它等于所有特征值之和；
• 类似的有，因为三角矩阵的特征值就是主对角线上的项，其行列式等于等于特征值的乘积（按代数重次计算出现次数）。

正规矩阵的一些子类的谱的位置是：

• 一个埃尔米特矩阵（A = A^*）的所有特征值是实数。进一步的有，所有正定矩阵（v^*Av > 0 for all vectors v）的所有特征值是正数；
• 所有斜埃尔米特矩阵（A = −A^*）的特征值是纯虚数；
• 所有酉矩阵（A^-1 = A^*）的特征值绝对值为1;

假设A是一个m×n矩阵，其中m ≤ n，而B是一个n×m矩阵。则BA有和AB相同的特征值加上n − m个等于0的特征值。

每个矩阵可以被赋予一个算子范数。算子范数是其特征值的模的上确界，因而也是它的谱半径。该范数直接和计算最大模的特征值的幂法直接相关。当一个矩阵是正规的，其算子范数是其特征值的最大模，并且独立于其定义域的范数。

共轭特征向量

一个共轭特征向量或者说共特征向量是一个在变换下成为其共轭乘以一个标量的向量，其中那个标量称为该线性变换的共轭特征值或者说共特征值。共轭特征变量和共轭特征值代表了和常规特征向量和特征值相同的信息和含义，但是在交替坐标系统被使用的时候出现。对应的方程是：

${\displaystyle Av=\lambda v^{*}\ }$

例如，在相干电磁散射理论中，线性变换A代表散射物体施行的作用，而特征向量表示电磁波的极化状态。在光学中，坐标系统按照波的观点定义，称为前向散射对齐（FSA），从而导致了常规的特征值方程，而在雷达中，坐标系统按照雷达的观点定义，称为后向散射对齐（BSA），从而给出了共轭特征值方程。

广义特征值

一个广义特征值（第二种意义）有如下形式

${\displaystyle Av=\lambda Bv\quad \quad }$

其中A和B为矩阵。其广义特征值（第二种意义）λ 可以通过求解如下方程得到

${\displaystyle \det(A-\lambda B)=0\ }$

形如${\displaystyle A-\lambda B}$的矩阵的集合，其中${\displaystyle \lambda }$是一个复数，称为一个“束（pencil）”。若B可逆，则最初的问题可以写作如下形式

${\displaystyle B^{-1}Av=\lambda v\quad \quad }$

也即标准的特征值问题。但是，在很多情况下施行逆操作是不可取的，而广义特征值问题应该如同其原始表述来求解。

如果A和B是实系数的对称矩阵，则特征值为实数。这在上面的第二种等价表述中并不明显，因为矩阵${\displaystyle B^{-1}A}$未必是对称的。

这里的一个例子是分子轨道应用如下。

系数为环中元素

在方矩阵A，其系数属于一个环的情况，λ称为一个右特征值如果存在一个列向量x使得Ax=λx，或者称为一个左特征值如果存在非零行向量y使得yA=yλ。

若环是可交换的，左特征值和右特征值相等，并简称为特征值。否则，例如当环是四元数集合的时候，它们可能是不同的。

无穷维空间

若向量空间是无穷维的，特征值的概念可以推广到谱的概念。谱是标量λ的集合，对于这些标量，${\displaystyle \left({\mathcal {T}}-\lambda \right)^{-1}}$没有定义，也就是说它们使得${\displaystyle {\mathcal {T}}-\lambda }$没有有界逆。

很明显，如果λ是T的特征值，λ位于T的谱内。一般来讲，反过来并不成立。在希尔伯特空间或者巴拿赫空间上有一些算子完全没有特征向量。这可以从下面的例子中看到。在希尔伯特空间${\displaystyle \ell ^{2}(\mathbf {Z} )}$(所有标量级数的空间，每个级数${\displaystyle \dots a_{-1},a_{0},a_{1},a_{2},\dots }$使得${\displaystyle \dots |a_{-1}|^{2}+|a_{0}|^{2}+|a_{1}|^{2}+|a_{2}|^{2}+\dots }$收敛)上的双向平移没有特征向量却有谱值。

在无穷维空间，有界算子的谱系总是非空的，这对无界自共轭算子也成立。通过检验谱测度，任何有界或无界的自共轭算子的谱可以分解为绝对连续，离散，和孤立部分。指数增长或者衰减是连续谱的例子，而振动弦驻波是离散谱例子。氢原子是两种谱都有出现的例子。氢原子的束缚态对应于谱的离散部分，而离子化状态用连续谱表示。

应用

薛定谔方程

图3、電子的機率密度繪圖。橫向展示不同的角量子數，豎向展示不同的能級（n）。束缚於氢原子内的电子的波函数可以视为氢原子的哈密顿算子的特征向量，同时也是角动量算子的一个特征向量。它们对应於能级（递增：n=1,2,3,...）和角动量（递增：s, p, d,...）的特征值。这里绘出了波函数绝对值的平方。更亮区域对应于位置的量子测量的更高機率密度。位於每幅图的中心是原子核，是一个质子

主条目：薛定谔方程

在量子力学中，不含时薛定谔方程是一个以微分算子代表的变换${\displaystyle T\,}$的特征值方程，能够描述一个粒子的量子行为：

${\displaystyle H\Psi _{E}=E\Psi _{E}\,}$

其中，${\displaystyle H\,}$是哈密顿算子，一个二阶微分算子，${\displaystyle \Psi _{E}\,}$是描述粒子的量子行为的波函数，对应于特征值${\displaystyle E\,}$的特征函数，该值可以解释为粒子的能量。

假设，我们只想寻找薛定谔方程的束缚态(bound state)解，那麼，可以在平方可积函数的空间中寻找${\displaystyle \Psi _{E}\,}$。由於这个空间是希尔伯特空间，有一个定义良好的标量积，我们可以引入一个基集合，然后表示${\displaystyle \Psi _{E}\,}$和${\displaystyle H\,}$为一个一维数组和一个矩阵。这样，我们能够用矩阵形式表达薛定谔方程。（图3表示氢原子哈密顿算子的最低能级特征函数。）

狄拉克标记经常在这个上下文中使用，以强调量子态${\displaystyle \Psi _{E}\,}$的态向量${\displaystyle |\Psi _{E}\rangle \,}$和它表示於位置空间的波函数${\displaystyle \Psi _{E}(x)\,}$之间的区别。采用狄拉克标记，薛定谔方程写为

${\displaystyle H|\Psi _{E}\rangle =E|\Psi _{E}\rangle \,}$

并称${\displaystyle |\Psi _{E}\rangle \,}$是${\displaystyle H\,}$的一个本征态（${\displaystyle H\,}$有时候在入门级课本中写作${\displaystyle {\hat {H}}\,}$），${\displaystyle H\,}$是一个自伴算子（参看可观察量）。在上述方程中，${\displaystyle H|\Psi _{E}\rangle \,}$理解为通过作用${\displaystyle H\,}$於${\displaystyle |\Psi _{E}\rangle \,}$得到的一个新的态向量。

分子轨域

在量子力学中，特别是在原子物理和分子物理中，在Hartree-Fock理论下，原子轨域和分子轨域可以定义为Fock算子的特征向量。相应的特征值通过Koopmans定理可以解释为电离势能。在这个情况下，特征向量一词可以用于更广泛的意义，因为Fock算子显式地依赖于轨道和它们地特征值。如果需要强调这个特点，可以称它为隐特征值方程。这样地方程通常采用迭代程序求解，在这个情况下称为自洽场方法。在量子化学中，经常会把Hartree-Fock方程通过非正交基集合来表达。这个特定地表达是一个广义特征值问题称为Roothaan方程。

因子分析

在因素分析中，一个協方差矩陣的特征向量对应于因素，而特征值是因素负载。因素分析是一种统计学技术，用于社会科学和市场分析、产品管理、运筹规划和其他处理大量数据的应用科学。其目标是用称为因素的少量的不可观测随机变量来解释在一些可观测随机变量中的变化。可观测随机变量用因素的线性组合来建模，再加上“残差项。

振動分析

懸臂樑的幾種振動模態
側向彎曲	扭轉彎曲	垂直彎曲

在對於多自由度機械結構作振動分析時，常常會遇到特徵值問題。經過仔細解析，求得的特徵值會給出振動的自然頻率，而特徵向量則會給出振動模態的振動行為。由於特徵向量的相互正交性質，允許對應的微分方程式能夠解耦合(decouple)，整個系統可以表示為特徵向量的線性總和。有限元分析是一種非常優良的方法，時常用來解析複雜結構的特徵值問題。

特征脸

图4. 特征脸是特征变量的例子

在图像处理中，脸部图像的处理可以看作分量为每个像素的灰度的向量。该向量空间的维数是像素的个数。一个标准化面部图形的一个大型数据集合的協方差矩陣的特征向量称为特征脸。它们对于将任何面部图像表达为它们的线性组合非常有用。特征脸提供了一种用于识别目的的数据压缩的方式。在这个应用中，一般只取那些最大特征值所对应的特征脸[11]。

慣性張量

採用直角坐標系的三個坐標軸為參考軸，一個剛體的慣性張量${\displaystyle {\mathcal {I}}\,}$，以矩陣形式表達為

${\displaystyle {\mathcal {I}}={\begin{bmatrix}I_{xx}&I_{xy}&I_{xz}\\I_{yx}&I_{yy}&I_{yz}\\I_{zx}&I_{zy}&I_{zz}\end{bmatrix}}\,}$ ；

其中，矩陣的元素以方程式表達為

${\displaystyle I_{xx}\ {\stackrel {\mathrm {def} }{=}}\ \int y^{2}+z^{2}\ dm\qquad \qquad I_{xy}=I_{yx}\ {\stackrel {\mathrm {def} }{=}}\ -\int xy\ dm\,}$、

${\displaystyle I_{yy}\ {\stackrel {\mathrm {def} }{=}}\ \int x^{2}+z^{2}\ dm\qquad \qquad I_{xz}=I_{zx}\ {\stackrel {\mathrm {def} }{=}}\ -\int xz\ dm\,}$、

${\displaystyle I_{zz}\ {\stackrel {\mathrm {def} }{=}}\ \int x^{2}+y^{2}\ dm\qquad \qquad I_{yz}=I_{zy}\ {\stackrel {\mathrm {def} }{=}}\ -\int yz\ dm\,}$，

${\displaystyle (x,\ y,\ z)\,}$是剛體內部的微小體積元${\displaystyle dm\,}$的位置。

慣性張量${\displaystyle {\mathcal {I}}\,}$是個實值的三維對稱矩陣，對角元素${\displaystyle I_{xx}\,}$、${\displaystyle I_{yy}\,}$、${\displaystyle I_{zz}\,}$分別為剛體對於x-軸、y-軸、z-軸的轉動慣量。非對角元素${\displaystyle I_{\alpha \beta },\alpha \neq \beta \,}$是剛體對於${\displaystyle \alpha \,}$-軸和${\displaystyle \beta \,}$-軸的慣量積。根据谱定理，可以使慣性張量成為一個對角矩陣[12]。所得到的三個特徵值必是正實值；三個特徵向量必定互相正交。

換另外一種方法，我們需要求解特徵方程式

${\displaystyle {\mathcal {I}}\ {\boldsymbol {\omega }}=\lambda \;{\boldsymbol {\omega }}\,}$，

也就是以下行列式等於零的的三次方程式：

${\displaystyle {\begin{vmatrix}I_{xx}-\lambda &I_{xy}&I_{xz}\\I_{yx}&I_{yy}-\lambda &I_{yz}\\I_{zx}&I_{zy}&I_{zz}-\lambda \end{vmatrix}}=0\,}$ 。

這方程式的三個根${\displaystyle \lambda _{1}\,}$、${\displaystyle \lambda _{2}\,}$、${\displaystyle \lambda _{3}\,}$都是正實的特徵值。將特徵值代入特徵方程式，再加上方向餘弦(directional cosine)方程式，

${\displaystyle \omega _{x}^{2}+\omega _{y}^{2}+\omega _{z}^{2}=1\,}$。就可以求到特徵向量${\displaystyle {\hat {\boldsymbol {\omega }}}_{1}\,}$、${\displaystyle {\hat {\boldsymbol {\omega }}}_{2}\,}$、${\displaystyle {\hat {\boldsymbol {\omega }}}_{3}\,}$。這些特徵向量都是剛體的慣量主軸；而這些特徵值則分別是剛體對於慣量主軸的主轉動慣量。

应力张量

在固体力学中，应力张量是对称的，因而可以分解为对角张量，其特征值位于对角线上，而特征向量可以作为基。因为它是对角阵，在这个定向中，应力张量没有剪切分量；它只有主分量。

图的特征值

在谱系图论中，一个图的特征值定义为图的邻接矩阵A的特征值，或者（更多的是）图的拉普拉斯算子矩阵${\displaystyle I-T^{-1/2}AT^{-1/2}}$，其中T是对角阵表示每个顶点的度数，在${\displaystyle T^{-1/2}}$中，0用于取代${\displaystyle 0^{-1/2}}$。图的主特征向量用于测量其顶点的中心度。Google的PageRank算法就是一个例子。www图的修正邻接矩阵的主特征向量的分量给出了页面评分。

相關條目

• 反特徵值理論
• 非线性特征值问题

注釋

1. 在这个上下文，只考虑从一个向量空间到自身的线性变换。
2. 因为所有线性变换保持零向量不变，它不作为一个特征向量。

参考文献

引用

1. Steven A. Leduc, Linear Algbra，第251-252页
2. Steven A. Leduc, Linear Algbra，第293页
3. Strang Gilbert, Introduction to Linear Algbra，第245页
4. Steven A. Leduc, Linear Algbra，第307-308页
5. Steven Roman, Advanced Linear Algbra，第189页
6. 李庆扬，王能超，易大义，《数值分析（第4版）》，第299-301页
7. Steven Roman,Advanced Linear Algbra，第186页
8. Strang Gilbert, Linear Algebra and its Applications，第245页
9. 王萼芳. 《高等代数教程》. 清华大学出版社. 1997. ISBN 9787302024781. ，第233-234页
10. Trefethen, Lloyd N.; Bau, David, Numerical Linear Algebra, SIAM: pp. 211ff, 1997, ISBN 9780898713619  引文格式1维护：冗余文本 (link) Lloyd N. Trefethen and David Bau, Numerical Linear Algebra（SIAM, 1997）
11. Xirouhakis, Y.; G.Votsis and A. Delopoulos, Estimation of 3D Motion and Structure of Human Faces (PDF), Proc. of European Robotics, Intelligent Systems and Control Conference (EURISCON), Athens, Greece, 1998 [2010-05-20], （原始内容存档 (PDF)于2020-12-03） 
12. O'Nan, Michael. Linear Algebra. USA: Harcourt Brace Jovanovich, Inc. 1971: pp. 361. ISBN 0-15-518558-6 （英语）.  引文格式1维护：冗余文本 (link)

书籍

• （英文） Beezer, Robert A., A first course in linear algebra, Free online book under GNU licence, University of Puget Sound: p. 518, 2006 [2010-05-20], ISBN 9781616100049, （原始内容存档于2008-03-10）  引文格式1维护：冗余文本 (link)
• （英文） Friedberg, Stephen H.; Insel, Arnold J.; Spence, Lawrence E., Linear algebra 2nd Edition, Englewood Cliffs, NJ 07632: Prentice Hall: p. 217f, 1989, ISBN 0-13-537102-3  引文格式1维护：冗余文本 (link)
• （英文） Golub, Gene H.; Van Loan, Charles F., chapter 7, 8, Matrix computations 3rd Edition, Johns Hopkins University Press, Baltimore, MD, 1996, ISBN 978-0-8018-5414-9  引文格式1维护：冗余文本 (link)
• （英文） Kuttler, Kenneth, An introduction to linear algebra (PDF), Online e-book in PDF format, Brigham Young University: p. 51, 2007 [2010-05-20], （原始内容存档 (PDF)于2008-08-07）  引文格式1维护：冗余文本 (link)
• （英文）Meyer, Carl D., chapter 7, Matrix analysis and applied linear algebra, Society for Industrial and Applied Mathematics (SIAM), Philadelphia, 2000, ISBN 978-0-89871-454-8 
• （英文） Korn, Granino A.; Korn, Theresa M., Mathematical Handbook for Scientists and Engineers: Definitions, Theorems, and Formulas for Reference and Review 2 Revised Edition, Dover Publications: p. 1152, 2000, ISBN 0-486-41147-8  引文格式1维护：冗余文本 (link)
• （英文） Gilbert Strang. Linear algebra and its applications. Thomson, Brooks/Cole, Belmont, CA. 2006. ISBN 9780534422004. 
• （英文）Roger A. Horn and Charles R. Johnson. Matrix Analysis. Cambridge University Press. 1985. ISBN 0-521-30586-1. 
• （英文） John B. Fraleigh and Raymond A. Beauregard. Linear Algebra 3^rd edition. Addison-Wesley Publishing Company. 1995. ISBN 0-201-83999-7.  引文格式1维护：冗余文本 (link)
• （英文） Claude Cohen-Tannoudji. Quantum Mechanics. Wiley. 1977. ISBN 0-471-16432-1. 
• （英文） Gilbert Strang. Introduction to Linear Algebra Third Edition. Wellesley Cambridge Pr. 2003. ISBN 978-0-961-40889-3.  引文格式1维护：冗余文本 (link)
• （英文） Steven A. Leduc. Linear Algebra Third Edition. Cliffs Notes. 1996. ISBN 978-0822053316.  引文格式1维护：冗余文本 (link)
• （英文）Steven Roman. Advanced Linear Algebra. Springer. 2005. ISBN 0-387-24766-1. 
• 李庆扬、王能超、易大义. 《数值分析（第4版）》. 清华大学出版社. ISBN 7302045615. 

外部連結

• （英文）麻省理工学院线性代数教程录像，2005年春季学期 （页面存档备份，存于互联网档案馆） - 参看Eigenvalues and Eigenvectors（特征值与特征向量）一课
• （英文）埃里克·韦斯坦因. 特征向量. MathWorld.  （页面存档备份，存于互联网档案馆）
• （英文）某些数学词汇最早已知的使用：E - 见特征向量和相关术语
• （英文）ARPACK （页面存档备份，存于互联网档案馆）求解大型特征值问题的FORTRAN子程序汇集
• （英文）Eigenvalue (of a matrix). PlanetMath. 
• （英文）特征值和特征向量的在线计算器 （页面存档备份，存于互联网档案馆）
• （英文）在线矩阵计算器可以在线计算特征值，特征向量和矩阵的其它分解。