|
 6是完全数 6是完全数
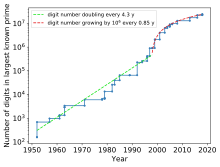 20世纪下半叶起已知最大质数位数对数图,这些已知最大质数大多是梅森素数 20世纪下半叶起已知最大质数位数对数图,这些已知最大质数大多是梅森素数
梅森素数与完全数是数论里关系密切的自然数。梅森素数以数学家、神学家、修士马兰·梅森命名,是能以2甲-1表示、且甲为正整数的质数,如梅森素数3就能写成22-1[1][2]。梅森素数在上述表达式对应的数甲一定是质数,但甲是质数不代表得出的结果就是梅森素数,如211-1=2047=23×89[3]。完全数是等于真因数之和的自然数,真因数即自然数除自身外的因数。如6就是完全数,因数分别是1、2、3、6且1+2+3=6。[2][4]
根据欧几里得部分证明、萊昂哈德·歐拉完全证明的歐幾里得-歐拉定理可知梅森素数与已知完全数一一对应:只有能换算成公式2甲-1×(2甲-1),且2甲 − 1是梅森素数的偶数是完全数。以甲=2为例,22-1=3为质数,22-1×(22-1)=2×3=6为完全数。[1][5][6]
梅森素数与完全数是否无穷尽目前还是未解决的数学问题[2][6],伦斯特拉-波默朗斯-瓦格斯塔夫猜想的主题便是梅森素数频率,推断比x小的梅森素数期望个数為(eγ/log2)×log log x,其中e是欧拉数,γ是欧拉常数,log是自然對數[7][8][9]。已经发现的完全数都是偶数,但尚未排除存在奇数完全数的可能。已證明奇完全数必滿足某些條件,如不小於101500[10]。
下表列出所有已知梅森素数、完全数及对应指数甲。截至2021年10月共发现51个梅森素数(及對應完全数),最大17个均由互联网梅森素数大搜索分布式计算项目发现。[2]新梅森素数是用卢卡斯-莱默检验法发现,这种梅森素数素性测试可用于二进制计算机[2]。
数字按从小到大排列,如果新发现比现有结果小的梅森素数则插入中间。序号后面的问号说明尚待验证。截至2021年10月,互联网梅森素数大搜索已经计算至甲=5820萬4879,即第48个梅森素数以前的所有自然数均已验证。[11]发现时间和发现人均指梅森素数,完全数按歐幾里得-歐拉定理计算。发现人列为“互联网梅森素数大搜索:姓名”说明此人拥有的设备采用互联网梅森素数大搜索找到该数。除前八个不超过十位外,后面的结果都非常长,最长的已有数千万位;下表仅列出前后各六位,中间以省略号表示。
梅森素数与完全数集合
GIMPS發現的梅森素数
最小未驗證梅森素數
梅森猜測的梅森質數
古代知道的梅森素数
拉爾夫·歐內斯特·鮑爾斯發現的梅森素数
唐納德·吉利斯發現的梅森質數
大衛·斯洛文斯基發現的梅森素数
下表列出了所有已知的梅森素数: A000668 A000668
下表列出了所有已知的梅森素数指數: A000043 A000043
| 序
|
甲
|
梅森素数
|
梅森素数位数
|
對應完全数
|
完全数位数
|
发现时间
|
发现人
|
发现方法
|
参考[12]
|
| 1
|
2
|
3
|
1
|
6
|
1
|
000000000100-01-01-0000古代[注 1]
|
古希腊数学家已经知晓
|
人手计算
|
[13][14][15]
|
| 2
|
3
|
7
|
1
|
28
|
2
|
[13][14][15]
|
| 3
|
5
|
31
|
2
|
496
|
3
|
[13][14][15]
|
| 4
|
7
|
127
|
3
|
8128
|
4
|
[13][14][15]
|
| 5
|
13
|
8191
|
4
|
33550336
|
8
|
000000001456-01-01-0000约1456年[注 2]
|
不明[注 3]
|
试除法
|
[14][15]
|
| 6
|
17
|
131071
|
6
|
8589869056
|
10
|
000000001588-01-01-00001588年[注 2]
|
皮特罗·卡塔尔迪
|
[2][18]
|
| 7
|
19
|
524287
|
6
|
137438691328
|
12
|
[2][18]
|
| 8
|
31
|
21億4748萬3647
|
10
|
230584……952128
|
19
|
000000001772-01-01-00001772年
|
萊昂哈德·歐拉
|
[19]
|
| 9
|
61
|
230京5843兆0092億1369萬3951
|
19
|
265845……842176
|
37
|
1883年11月
|
伊万·波佛辛
|
卢卡斯数列
|
[20]
|
| 10
|
89
|
618970……562111
|
27
|
191561……169216
|
54
|
1911年6月
|
拉尔夫·欧内斯特·鲍尔斯
|
卢卡斯数列
|
[21]
|
| 11
|
107
|
162259……288127
|
33
|
131640……728128
|
65
|
1914年6月
|
[22]
|
| 12
|
127
|
170141183460469231731687303715884105727
|
39
|
144740……152128
|
77
|
1876年1月
|
爱德华·卢卡斯
|
卢卡斯数列
|
[23]
|
| 13
|
521
|
686479……057151
|
157
|
235627……646976
|
314
|
1952年1月
|
拉斐爾·米切爾·羅賓遜
|
计算机采用卢卡斯-莱默检验法
|
[24]
|
| 14
|
607
|
531137……728127
|
183
|
141053……328128
|
366
|
[24]
|
| 15
|
1279
|
104079……729087
|
386
|
541625……291328
|
770
|
1952年6月
|
[25]
|
| 16
|
2203
|
147597……771007
|
664
|
108925……782528
|
1327
|
1952年10月
|
[26]
|
| 17
|
2281
|
446087……836351
|
687
|
994970……915776
|
1373
|
[26]
|
| 18
|
3217
|
259117……315071
|
969
|
335708……525056
|
1937
|
1957年9月
|
汉斯·黎瑟尔
|
[27]
|
| 19
|
4253
|
190797……484991
|
1281
|
182017……377536
|
2561
|
1961年11月
|
亚历山大·赫维茨
|
[28]
|
| 20
|
4423
|
285542……580607
|
1332
|
407672……534528
|
2663
|
[28]
|
| 21
|
9689
|
478220……754111
|
2917
|
114347……577216
|
5834
|
1963年5月
|
唐纳德·吉利斯
|
计算机采用卢卡斯-莱默检验法
|
[29]
|
| 22
|
9941
|
346088……463551
|
2993
|
598885……496576
|
5985
|
[29]
|
| 23
|
11213
|
281411……392191
|
3376
|
395961……086336
|
6751
|
1963年6月
|
[29]
|
| 24
|
19937
|
431542……041471
|
6002
|
931144……942656
|
12003
|
1971年3月
|
计算机采用卢卡斯-莱默检验法
|
布萊恩特·塔克曼
|
[30]
|
| 25
|
21701
|
448679……882751
|
6533
|
100656……605376
|
13066
|
1978年10月
|
蓝登·克特·诺尔、劳拉·尼克尔
|
[31]
|
| 26
|
23209
|
402874……264511
|
6987
|
811537……666816
|
13973
|
1979年2月
|
蓝登·克特·诺尔
|
[31]
|
| 27
|
44497
|
854509……228671
|
13395
|
365093……827456
|
26790
|
1979年4月
|
计算机采用卢卡斯-莱默检验法
|
哈里·尼尔森、大卫·斯洛文斯基
|
[32][33]
|
| 28
|
86243
|
536927……438207
|
25962
|
144145……406528
|
51924
|
1982年9月
|
大卫·斯洛文斯基
|
[34]
|
| 29
|
11萬0503
|
521928……515007
|
33265
|
136204……862528
|
66530
|
1988年1月
|
计算机采用卢卡斯-莱默检验法
|
沃尔特·科尔奎特、卢克·韦尔什
|
[35][36]
|
| 30
|
13萬2049
|
512740……061311
|
39751
|
131451……550016
|
79502
|
1983年9月
|
计算机采用卢卡斯-莱默检验法
|
大卫·斯洛文斯基等人(克雷公司)
|
[37]
|
| 31
|
21萬6091
|
746093……528447
|
65050
|
278327……880128
|
13萬0100
|
1985年9月
|
[38][39]
|
| 32
|
75萬6839
|
174135……677887
|
22萬7832
|
151616……731328
|
45萬5663
|
1992年2月
|
[40]
|
| 33
|
85萬9433
|
129498……142591
|
25萬8716
|
838488……167936
|
51萬7430
|
1994年1月
|
[41]
|
| 34
|
125萬7787
|
412245……366527
|
37萬8632
|
849732……704128
|
75萬7263
|
1996年9月
|
[42][43]
|
| 35
|
139萬8269
|
814717……315711
|
42萬0921
|
331882……375616
|
84萬1842
|
1996年11月
|
计算机采用卢卡斯-莱默检验法
|
互联网梅森素数大搜索:乔尔·阿蒙古德
|
[44]
|
| 36
|
297萬6221
|
623340……201151
|
89萬5932
|
194276……462976
|
179萬1864
|
1997年8月
|
互联网梅森素数大搜索:戈登·斯彭斯
|
[45]
|
| 37
|
302萬1377
|
127411……694271
|
90萬9526
|
811686……457856
|
181萬9050
|
1998年1月
|
互联网梅森素数大搜索:罗兰·克拉克森
|
[46]
|
| 38
|
697萬2593
|
437075……193791
|
209萬8960
|
955176……572736
|
419萬7919
|
1999年6月
|
互联网梅森素数大搜索:纳扬·哈吉拉特瓦拉
|
[47]
|
| 39
|
1346萬6917
|
924947……259071
|
405萬3946
|
427764……021056
|
810萬7892
|
2001年11月
|
互联网梅森素数大搜索:迈克尔·卡梅隆
|
[48]
|
| 40
|
2099萬6011
|
125976……682047
|
632萬0430
|
793508……896128
|
1264萬0858
|
2003年11月
|
互联网梅森素数大搜索:迈克尔·谢弗
|
[49]
|
| 41
|
2403萬6583
|
299410……969407
|
723萬5733
|
448233……950528
|
1447萬1465
|
2004年5月
|
互联网梅森素数大搜索:乔希·芬德利
|
[50]
|
| 42
|
2596萬4951
|
122164……077247
|
781萬6230
|
746209……088128
|
1563萬2458
|
2005年2月
|
互联网梅森素数大搜索:马丁·诺瓦克
|
[51]
|
| 43
|
3040萬2457
|
315416……943871
|
915萬2052
|
497437……704256
|
1830萬4103
|
2005年12月
|
互联网梅森素数大搜索:柯蒂斯·库珀、史蒂文·布恩
|
[52]
|
| 44
|
3258萬2657
|
124575……967871
|
980萬8358
|
775946……120256
|
1961萬6714
|
2006年9月
|
[53]
|
| 45
|
3715萬6667
|
202254……220927
|
1118萬5272
|
204534……480128
|
2237萬0543
|
2008年9月
|
互联网梅森素数大搜索:汉斯-迈克尔·埃尔维尼奇
|
[54]
|
| 46
|
4264萬3801
|
169873……314751
|
1283萬7064
|
144285……253376
|
2567萬4127
|
2009年6月
|
互联网梅森素数大搜索:奥德·麦格纳·斯特林莫
|
[55]
|
| 47
|
43112609
|
316470……152511
|
1297萬8189
|
500767……378816
|
2595萬6377
|
2008年8月
|
互联网梅森素数大搜索:埃德森·史密斯
|
[54][56]
|
| 48
|
5788萬5161
|
581887……285951
|
1742萬5170
|
169296……130176
|
3485萬0340
|
2013年1月
|
互联网梅森素数大搜索:柯蒂斯·库珀
|
[57][58]
|
| 不适用
|
6868萬9253
|
最低未验证里程碑(截至西元2024年6月23日)[注 4]
|
| 49?
|
7420萬7281
|
300376……436351
|
2233萬8618
|
451129……315776
|
4467萬7235
|
2016年1月
|
互联网梅森素数大搜索:柯蒂斯·库珀
|
计算机采用卢卡斯-莱默检验法
|
[59][60]
|
| 50?
|
7723萬2917
|
467333……179071
|
2324萬9425
|
109200……301056
|
4649萬8850
|
2017年12月
|
互联网梅森素数大搜索:乔纳森·佩斯
|
[61][62]
|
| 51?
|
8258萬9933
|
148894……902591
|
2486萬2048
|
110847……207936
|
4972萬4095
|
000000002018-12-01-00002018年12月
|
互联网梅森素数大搜索:帕特里克·拉罗什
|
[63][64]
|
| 不适用
|
1億1748萬5899
|
最低未测试里程碑(截至西元2024年6月23日)[注 4]
|
注释
参考资料
- ^ 1.0 1.1 Stillwell, John. Mathematics and Its History. Undergraduate Texts in Mathematics. Springer Science+Business Media. 2010: 40 [2021-11-01]. ISBN 978-1-4419-6052-8. (原始内容存档于2021-10-13).
- ^ 2.0 2.1 2.2 2.3 2.4 2.5 2.6 Caldwell, Chris K. Mersenne Primes: History, Theorems and Lists. PrimePages. [2021-10-27]. (原始内容存档于2021-10-27).
- ^ Caldwell, Chris K. If 2n-1 is prime, then so is n. PrimePages. [2021-11-01]. (原始内容存档于2021-10-27).
- ^ Prielipp, Robert W. Perfect Numbers, Abundant Numbers, and Deficient Numbers. The Mathematics Teacher. 1970, 63 (8): 692–696. JSTOR 27958492. doi:10.5951/MT.63.8.0692 –通过JSTOR.
- ^ Caldwell, Chris K. Characterizing all even perfect numbers. PrimePages. [2021-11-01]. (原始内容存档于2021-10-27).
- ^ 6.0 6.1 Crilly, Tony. Perfect numbers. 50 mathematical ideas you really need to know. Quercus Publishing. 2007 [2021-11-01]. ISBN 978-1-84724-008-8. (原始内容存档于2021-10-13).
- ^ Caldwell, Chris K. Heuristics Model for the Distribution of Mersennes. PrimePages. [2021-11-01]. (原始内容存档于2021-10-19).
- ^ Wagstaff, Samuel S. Divisors of Mersenne numbers. Mathematics of Computation. 1983-01, 40 (161): 385. ISSN 0025-5718. doi:10.1090/S0025-5718-1983-0679454-X.
- ^ Pomerance, Carl. Recent developments in primality testing. The Mathematical Intelligencer. 1981-09, 3 (3): 97–105. ISSN 0343-6993. S2CID 121750836. doi:10.1007/BF03022861.
- ^ Ochem, Pascal; Rao, Michaël. Odd perfect numbers are greater than 101500. Mathematics of Computation. 2012-01-30, 81 (279): 1869–1877. ISSN 0025-5718. doi:10.1090/S0025-5718-2012-02563-4.
- ^ 11.0 11.1 GIMPS Milestones Report. Great Internet Mersenne Prime Search. [2021-11-01]. (原始内容存档于2021-10-31).
- ^ 以下文献可以找到所有结果:
- ^ 13.0 13.1 13.2 13.3 Joyce, David E. Euclid's Elements, Book IX, Proposition 36. Department of Mathematics and Computer Science. Worcester, MA: Clark University. [2021-11-01]. (原始内容存档于2021-06-17).
- ^ 14.0 14.1 14.2 14.3 14.4 14.5 Dickson, Leonard Eugene. History of the Theory of Numbers, Vol. I. Carnegie Institution of Washington. 1919: 4–6 [2021-11-01]. (原始内容存档于2021-11-04).
- ^ 15.0 15.1 15.2 15.3 15.4 Smith, David Eugene. History of Mathematics: Volume II. Dover. 1925: 21 [2021-11-01]. ISBN 978-0-486-20430-7.
- ^ O'Connor, John J.; Robertson, Edmund F. Perfect numbers. MacTutor History of Mathematics archive. [2021-11-01]. (原始内容存档于2021-10-23).
- ^ 'Calendarium ecclesiasticum – BSB Clm 14908'. Bavarian State Library. [2021-11-01]. (原始内容存档于2021-10-28).
- ^ 18.0 18.1 Cataldi, Pietro Antonio. Trattato de' numeri perfetti di Pietro Antonio Cataldo. Presso di Heredi di Giouanni Rossi. 1603 [2021-11-01]. (原始内容存档于2021-11-04).
- ^ Euler, Leonhard. Extrait d'un lettre de M. Euler le pere à M. Bernoulli concernant le Mémoire imprimé parmi ceux de 1771, p 318. Nouveaux Mémoires de l'académie royale des sciences de Berlin. 1772, 1772: 35–36 [2021-11-01]. (原始内容存档于2020-10-15) –通过Euler Archive.
- ^ Sur un nouveau nombre premier, annoncé par le père Pervouchine. Bulletin de l'Académie impériale des sciences de St.-Pétersbourg. 1887-01-27, 31: 532–533 [2021-11-01]. (原始内容存档于2021-10-13) –通过Biodiversity Heritage Library.
- ^ Powers, R. E. The Tenth Perfect Number. The American Mathematical Monthly. 1911-11, 18 (11): 195–197. JSTOR 2972574. doi:10.2307/2972574.
- ^ Records of Proceedings at Meetings. Proceedings of the London Mathematical Society. 1914, s2–13 (1): iv–xl. doi:10.1112/plms/s2-13.1.1-s.
- ^ Lucas, Édouard. Note sur l'application des séries récurrentes à la recherche de la loi de distribution des nombres premier. Comptes rendus de l'Académie des Sciences. 1876, 82: 165–167 [2021-11-01]. (原始内容存档于2021-10-13).
- ^ 24.0 24.1 Notes. Mathematics of Computation. 1952-01, 6 (37): 58–61. ISSN 0025-5718. doi:10.1090/S0025-5718-52-99405-2.
- ^ Notes. Mathematics of Computation. 1952-07, 6 (39): 204. ISSN 0025-5718. doi:10.1090/S0025-5718-52-99389-7.
- ^ 26.0 26.1 Notes. Mathematics of Computation. 1953-01, 7 (41): 67–72. ISSN 0025-5718. doi:10.1090/S0025-5718-53-99372-7.
- ^ Riesel, Hans. A New Mersenne Prime. Mathematics of Computation. 1958-01, 12 (61): 60. doi:10.1090/S0025-5718-58-99282-2
 . .
- ^ 28.0 28.1 Hurwitz, Alexander. New Mersenne primes. Mathematics of Computation. 1962-04, 16 (78): 249. ISSN 0025-5718. doi:10.1090/S0025-5718-1962-0146162-X.
- ^ 29.0 29.1 29.2 Gillies, Donald B. Three new Mersenne primes and a statistical theory. Mathematics of Computation. 1964-01, 18 (85): 93–97. JSTOR 2003409. doi:10.1090/S0025-5718-1964-0159774-6
 . .
- ^ Tuckerman, Bryant. The 24th Mersenne Prime. Proceedings of the National Academy of Sciences. 1971-10, 68 (10): 2319–2320. Bibcode:1971PNAS...68.2319T. PMC 389411
 . PMID 16591945. doi:10.1073/pnas.68.10.2319 . PMID 16591945. doi:10.1073/pnas.68.10.2319  . .
- ^ 31.0 31.1 Noll, Landon Curt; Nickel, Laura. The 25th and 26th Mersenne primes. Mathematics of Computation. 1980-10, 35 (152): 1387. JSTOR 2006405. doi:10.1090/S0025-5718-1980-0583517-4
 . .
- ^ Slowinski, David. Searching for the 27th Mersenne prime. Journal of Recreational Mathematics. 1978, 11 (4): 258–261.
- ^ Science Watch: A New Prime Number. The New York Times. 1979-06-05 [2021-11-01]. (原始内容存档于2021-11-02).
- ^ Announcements. The Mathematical Intelligencer. 1983-03, 5 (1): 60. ISSN 0343-6993. doi:10.1007/BF03023507.
- ^ Peterson, I. Priming for a Lucky Strike. Science News. 1988-02-06, 133 (6): 85. JSTOR 3972461. doi:10.2307/3972461.
- ^ Colquitt, W. N.; Welsh, L. A new Mersenne prime. Mathematics of Computation. 1991-04, 56 (194): 867. Bibcode:1991MaCom..56..867C. JSTOR 2008415. doi:10.1090/S0025-5718-1991-1068823-9
 . .
- ^ Number is largest prime found yet.. The Globe and Mail. 1983-09-24.

- ^ Peterson, I. Prime Time for Supercomputers. Science News. 1985-09-28, 128 (13): 199. JSTOR 3970245. doi:10.2307/3970245.
- ^ Dembart, Lee. Supercomputer Comes Up With Whopping Prime Number. Los Angeles Times. 1985-09-17 [2021-11-01]. (原始内容存档于2021-11-02).
- ^ Maddox, John. The endless search for primality. Nature. 1992-03-26, 356 (6367): 283 [2021-11-01]. Bibcode:1992Natur.356..283M. ISSN 1476-4687. S2CID 4327045. doi:10.1038/356283a0. (原始内容存档于2021-10-29).
- ^ Largest Known Prime Number Discovered on Cray Research Supercomputer. PR Newswire. 1994-01-10 [2021-11-01]. (原始内容存档于2021-11-04) –通过Gale.
- ^ Caldwell, Chris K. A Prime of Record Size! 21257787-1. PrimePages. [2021-11-01]. (原始内容存档于2021-10-05).
- ^ Gillmor, Dan. Crunching numbers: Researchers come up with prime math discovery. Knight Ridder. 1996-09-03 [2021-11-01] –通过Gale.
- ^ GIMPS Discovers 35th Mersenne Prime, 21,398,269-1 is now the Largest Known Prime.. Great Internet Mersenne Prime Search. 1996-11-12 [2021-11-01]. (原始内容存档于2021-10-17).
- ^ GIMPS Discovers 36th Mersenne Prime, 22,976,221-1 is now the Largest Known Prime.. Great Internet Mersenne Prime Search. 1997-09-01 [2021-11-01]. (原始内容存档于2020-06-07).
- ^ GIMPS Discovers 37th Mersenne Prime, 23,021,377-1 is now the Largest Known Prime.. Great Internet Mersenne Prime Search. 1998-02-02 [2021-11-01]. (原始内容存档于2020-06-07).
- ^ GIMPS Discovers 38th Mersenne Prime 26,972,593-1 is now the Largest Known Prime.. Great Internet Mersenne Prime Search. 1999-06-30 [2021-11-01]. (原始内容存档于2020-06-07).
- ^ GIMPS Discovers 39th Mersenne Prime, 213,466,917-1 is now the Largest Known Prime.. Great Internet Mersenne Prime Search. 2001-12-06 [2021-11-01]. (原始内容存档于2020-06-07).
- ^ GIMPS Discovers 40th Mersenne Prime, 220,996,011-1 is now the Largest Known Prime.. Great Internet Mersenne Prime Search. 2003-02-02 [2021-11-01]. (原始内容存档于2020-06-07).
- ^ GIMPS Discovers 41st Mersenne Prime, 224,036,583-1 is now the Largest Known Prime.. Great Internet Mersenne Prime Search. 2004-05-28 [2021-11-01]. (原始内容存档于2021-01-29).
- ^ GIMPS Discovers 42nd Mersenne Prime, 225,964,951-1 is now the Largest Known Prime.. Great Internet Mersenne Prime Search. 2005-02-27 [2021-11-01]. (原始内容存档于2021-03-14).
- ^ GIMPS Discovers 43rd Mersenne Prime, 230,402,457-1 is now the Largest Known Prime.. Great Internet Mersenne Prime Search. 2005-12-24 [2021-11-01]. (原始内容存档于14 March 2021).
- ^ GIMPS Discovers 44th Mersenne Prime, 232,582,657-1 is now the Largest Known Prime.. Great Internet Mersenne Prime Search. 2006-09-11 [2021-11-01]. (原始内容存档于2021-10-17).
- ^ 54.0 54.1 GIMPS Discovers 45th and 46th Mersenne Primes, 243,112,609-1 is now the Largest Known Prime.. Great Internet Mersenne Prime Search. 2008-09-15 [2021-11-01]. (原始内容存档于2021-10-05).
- ^ GIMPS Discovers 47th Mersenne Prime. Great Internet Mersenne Prime Search. 2009-04-12 [2021-11-01]. (原始内容存档于2021-10-06).
- ^ Maugh, Thomas H. Rare prime number found. Los Angeles Times. 2008-09-27 [2021-11-01]. (原始内容存档于2021-10-29).
- ^ GIMPS Discovers 48th Mersenne Prime, 257,885,161-1 is now the Largest Known Prime.. Great Internet Mersenne Prime Search. 2013-02-05 [2021-11-01]. (原始内容存档于2021-10-17).
- ^ Yirka, Bob. University professor discovers largest prime number to date. phys.org. 2013-02-06 [2021-11-01]. (原始内容存档于2021-10-29).
- ^ GIMPS Project Discovers Largest Known Prime Number: 274,207,281-1. Great Internet Mersenne Prime Search. 2016-01-19 [2021-11-01]. (原始内容存档于2021-10-05).
- ^ Largest known prime number discovered in Missouri -GB. BBC News. 2016-01-20 [2021-11-01]. (原始内容存档于2021-08-21).
- ^ GIMPS Project Discovers Largest Known Prime Number: 277,232,917-1. Great Internet Mersenne Prime Search. 2018-01-03 [2021-11-01]. (原始内容存档于2021-10-17).
- ^ Lamb, Evelyn. Why You Should Care About a Prime Number That's 23,249,425 Digits Long. Slate Magazine. 2018-01-04 [2021-11-01]. (原始内容存档于2021-10-27).
- ^ GIMPS Discovers Largest Known Prime Number: 282,589,933-1. Great Internet Mersenne Prime Search. 2018-12-21 [2021-11-01]. (原始内容存档于2021-10-17).
- ^ Palca, Joe. The World Has A New Largest-Known Prime Number. NPR. 2018-12-21 [2021-11-01]. (原始内容存档于2021-07-30).
外部链接
|

