Trong toán học , một chuỗi là một tổng hình thức các số hạng của một dãy số vô hạn .
Cho một dãy vô hạn
(
a
1
,
a
2
,
a
3
,
…
)
,
{\displaystyle (a_{1},a_{2},a_{3},\dots ),}
tổng thành phần thứ n của nó S n n số hạng đầu tiên của chuỗi. Tức là,
S
n
=
∑
k
=
1
n
a
k
.
{\displaystyle S_{n}=\sum _{k=1}^{n}a_{k}.}
Một chuỗi được gọi là hội tụ nếu dãy các tổng thành phần của nó
(
S
1
,
S
2
,
S
3
,
…
)
{\displaystyle (S_{1},S_{2},S_{3},\dots )}
giới hạn ; điều đó có nghĩa là các tổng thành phần dần dần tiến gần hơn và gần hơn đến một số xác định.
Chính xác hơn, một chuỗi là hội tụ, nếu tồn tại một số xác định
ℓ
{\displaystyle \ell }
ε
{\displaystyle \varepsilon }
số nguyên (đủ lớn)
N
{\displaystyle N}
n
≥
N
{\displaystyle n\geq N}
|
S
n
−
ℓ
|
<
ε
.
{\displaystyle \left|S_{n}-\ell \right\vert <\varepsilon .}
Nếu chuỗi hội tụ, số
ℓ
{\displaystyle \ell }
tổng của chuỗi .
Bất kỳ chuỗi nào không hội tụ được gọi là phân kỳ.
Chuỗi nghịch đảo của các số nguyên dương là một chuỗi phân kỳ (cũng được gọi là chuỗi điều hòa ):
1
1
+
1
2
+
1
3
+
1
4
+
1
5
+
1
6
+
⋯
→
∞
.
{\displaystyle {1 \over 1}+{1 \over 2}+{1 \over 3}+{1 \over 4}+{1 \over 5}+{1 \over 6}+\cdots \rightarrow \infty .}
Chuỗi đan dấu các nghịch đảo của các số nguyên dương là một chuỗi hội tụ (chuỗi điều hòa đan dấu):
1
1
−
1
2
+
1
3
−
1
4
+
1
5
−
⋯
=
ln
(
2
)
{\displaystyle {1 \over 1}-{1 \over 2}+{1 \over 3}-{1 \over 4}+{1 \over 5}-\cdots =\ln(2)}
Chuỗi nghịch đảo của các số nguyên tố là một chuỗi phân kỳ:
1
2
+
1
3
+
1
5
+
1
7
+
1
11
+
1
13
+
⋯
→
∞
.
{\displaystyle {1 \over 2}+{1 \over 3}+{1 \over 5}+{1 \over 7}+{1 \over 11}+{1 \over 13}+\cdots \rightarrow \infty .}
Chuỗi nghịch đảo của các số tam giác là một chuỗi hội tụ:
1
1
+
1
3
+
1
6
+
1
10
+
1
15
+
1
21
+
⋯
=
2.
{\displaystyle {1 \over 1}+{1 \over 3}+{1 \over 6}+{1 \over 10}+{1 \over 15}+{1 \over 21}+\cdots =2.}
Chuỗi nghịch đảo của các giai thừa là một chuỗi hội tụ (xem e ):
1
1
+
1
1
+
1
2
+
1
6
+
1
24
+
1
120
+
⋯
=
e
.
{\displaystyle {\frac {1}{1}}+{\frac {1}{1}}+{\frac {1}{2}}+{\frac {1}{6}}+{\frac {1}{24}}+{\frac {1}{120}}+\cdots =e.}
Chuỗi nghịch đảo của các số chính phương là một chuỗi hội tụ (bài toán Basel):
1
1
+
1
4
+
1
9
+
1
16
+
1
25
+
1
36
+
⋯
=
π
2
6
.
{\displaystyle {1 \over 1}+{1 \over 4}+{1 \over 9}+{1 \over 16}+{1 \over 25}+{1 \over 36}+\cdots ={\pi ^{2} \over 6}.}
Chuỗi nghịch đảo của các lũy thừa cơ số 2 là một chuỗi hội tụ:
1
1
+
1
2
+
1
4
+
1
8
+
1
16
+
1
32
+
⋯
=
2.
{\displaystyle {1 \over 1}+{1 \over 2}+{1 \over 4}+{1 \over 8}+{1 \over 16}+{1 \over 32}+\cdots =2.}
Chuỗi nghịch đảo các lũy thừa cơ số n là một chuỗi hội tụ:
1
1
+
1
n
+
1
n
2
+
1
n
3
+
1
n
4
+
1
n
5
+
⋯
=
n
n
−
1
.
{\displaystyle {1 \over 1}+{1 \over n}+{1 \over n^{2}}+{1 \over n^{3}}+{1 \over n^{4}}+{1 \over n^{5}}+\cdots ={n \over n-1}.}
Chuỗi đan dấu các nghịch đảo của lũy thừa cơ số 2 là một chuỗi hội tụ:
1
1
−
1
2
+
1
4
−
1
8
+
1
16
−
1
32
+
⋯
=
2
3
.
{\displaystyle {1 \over 1}-{1 \over 2}+{1 \over 4}-{1 \over 8}+{1 \over 16}-{1 \over 32}+\cdots ={2 \over 3}.}
Chuỗi đan dấu các nghịch đảo của lũy thừa cơ số n là một chuội hội tụ:
1
1
−
1
n
+
1
n
2
−
1
n
3
+
1
n
4
−
1
n
5
+
⋯
=
n
n
+
1
.
{\displaystyle {1 \over 1}-{1 \over n}+{1 \over n^{2}}-{1 \over n^{3}}+{1 \over n^{4}}-{1 \over n^{5}}+\cdots ={n \over n+1}.}
Chuỗi nghịch đảo của các số Fibonacci là một chuỗi hội tụ (xem ψ ):
1
1
+
1
1
+
1
2
+
1
3
+
1
5
+
1
8
+
⋯
=
ψ
.
{\displaystyle {\frac {1}{1}}+{\frac {1}{1}}+{\frac {1}{2}}+{\frac {1}{3}}+{\frac {1}{5}}+{\frac {1}{8}}+\cdots =\psi .}
Có một số phương pháp xác định xem một chuỗi hội tụ hay phân kỳ, được gọi là các tiêu chuẩn hội tụ .
Nếu chuỗi màu xanh,
Σ
b
n
{\displaystyle \Sigma b_{n}}
Σ
a
n
{\displaystyle \Sigma a_{n}}
Σ
a
n
{\displaystyle \Sigma a_{n}}
Σ
b
n
{\displaystyle \Sigma b_{n}}
Tiêu chuẩn so sánh . Nếu,
với mọi n ,
0
≤
a
n
≤
b
n
{\displaystyle 0\leq \ a_{n}\leq \ b_{n}}
∑
n
=
1
∞
b
n
{\displaystyle \sum _{n=1}^{\infty }b_{n}}
∑
n
=
1
∞
a
n
{\displaystyle \sum _{n=1}^{\infty }a_{n}}
Nếu,
với mọi n ,
0
≤
b
n
≤
a
n
{\displaystyle 0\leq \ b_{n}\leq \ a_{n}}
∑
n
=
1
∞
b
n
{\displaystyle \sum _{n=1}^{\infty }b_{n}}
∑
n
=
1
∞
a
n
{\displaystyle \sum _{n=1}^{\infty }a_{n}}
Tiêu chuẩn D'Alembert (hay tiêu chuẩn tỷ lệ ). Giả sử rằng với mọi n ,
a
n
{\displaystyle a_{n}}
r
{\displaystyle r}
lim
n
→
∞
|
a
n
+
1
a
n
|
=
r
.
{\displaystyle \lim _{n\to \infty }\left|{\frac {a_{n+1}}{a_{n}}}\right|=r.}
Nếu r <1, thì chuỗi hội tụ tuyệt đối. Nếu r > 1,r = 1,
Tiêu chuẩn Cauchy (hay tiêu chuẩn căn thức ). Giả sử rằng các số hạng của chuỗi là không âm . Xác định r như sau:
r
=
lim sup
n
→
∞
|
a
n
|
n
,
{\displaystyle r=\limsup _{n\rightarrow \infty }{\sqrt[{n}]{|a_{n}|}},}
Nếu r <1, thì chuỗi hội tụ. Nếu r > 1,r = 1,
Tiêu chuẩn tích phân Cauchy .Giả sử
f
(
n
)
=
a
n
{\displaystyle f(n)=a_{n}}
f
{\displaystyle f}
hàm số dương đơn điệu giảm . Nếu
∫
1
∞
f
(
x
)
d
x
=
lim
t
→
∞
∫
1
t
f
(
x
)
d
x
<
∞
,
{\displaystyle \int _{1}^{\infty }f(x)\,dx=\lim _{t\to \infty }\int _{1}^{t}f(x)\,dx<\infty ,}
thì chuỗi hội tụ. Nếu tích phân phân kỳ thì chuỗi phân kỳ.
Tiêu chuẩn so sánh giới hạn . Nếu
{
a
n
}
,
{
b
n
}
>
0
{\displaystyle \left\{a_{n}\right\},\left\{b_{n}\right\}>0}
lim
n
→
∞
a
n
b
n
{\displaystyle \lim _{n\to \infty }{\frac {a_{n}}{b_{n}}}}
∑
n
=
1
∞
a
n
{\displaystyle \sum _{n=1}^{\infty }a_{n}}
khi và chỉ khi
∑
n
=
1
∞
b
n
{\displaystyle \sum _{n=1}^{\infty }b_{n}}
Tiêu chuẩn Leibniz
∑
n
=
1
∞
a
n
(
−
1
)
n
{\displaystyle \sum _{n=1}^{\infty }a_{n}(-1)^{n}}
{
a
n
}
{\displaystyle \left\{a_{n}\right\}}
giảm đơn điệu và có giới hạn bằng 0 ở vô cực thì chuỗi hội tụ.
Dấu hiệu Abel
Dấu hiệu Dirichlet
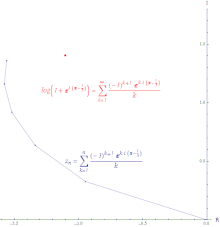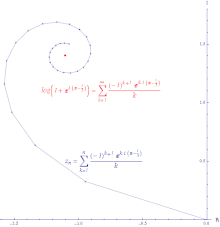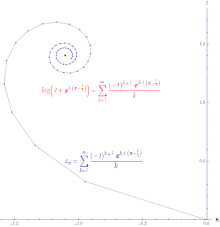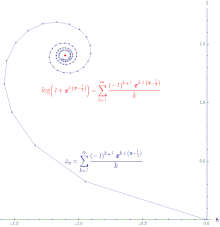
Minh họa sự hội tụ có điều kiện của chuỗi lũy thừa của log(z +1) gần điểm 0 được tính tại z = exp((π−1 ⁄3 i ). Với một dãy bất kỳ
{
a
1
,
a
2
,
a
3
,
…
}
{\displaystyle \left\{a_{1},\ a_{2},\ a_{3},\dots \right\}}
a
n
≤
|
a
n
|
{\displaystyle a_{n}\leq \ \left|a_{n}\right\vert }
n . Vì thế,
∑
n
=
1
∞
a
n
≤
∑
n
=
1
∞
|
a
n
|
.
{\displaystyle \sum _{n=1}^{\infty }a_{n}\leq \ \sum _{n=1}^{\infty }\left|a_{n}\right\vert .}
Điều này có nghĩa là (theo dấu hiệu so sánh) nếu
∑
n
=
1
∞
|
a
n
|
{\displaystyle \sum _{n=1}^{\infty }\left|a_{n}\right\vert }
∑
n
=
1
∞
a
n
{\displaystyle \sum _{n=1}^{\infty }a_{n}}
Nếu chuỗi
∑
n
=
1
∞
|
a
n
|
{\displaystyle \sum _{n=1}^{\infty }\left|a_{n}\right\vert }
∑
n
=
1
∞
a
n
{\displaystyle \sum _{n=1}^{\infty }a_{n}}
hội tụ tuyệt đối . Một dãy hội tụ tuyệt đối là dãy mà độ dài đoạn thẳng tạo ra khi nối lại tất cả các phần tăng thêm của tổng riêng có độ dài hữu hạn. Chuỗi lũy thừa của hàm mũ hội tụ tuyệt đối ở mọi nơi.
Nếu chuỗi
∑
n
=
1
∞
a
n
{\displaystyle \sum _{n=1}^{\infty }a_{n}}
∑
n
=
1
∞
|
a
n
|
{\displaystyle \sum _{n=1}^{\infty }\left|a_{n}\right\vert }
∑
n
=
1
∞
a
n
{\displaystyle \sum _{n=1}^{\infty }a_{n}}
hội tụ có điều kiện . Đoạn đường tạo ra khi nối các tổng riêng của một chuỗi hội tụ có điều kiện có độ dài vô hạn. Thí dụ, chuỗi lũy thừa của hàm logarit là hội tụ có điều kiện.
Định lỹ chuỗi Riemann khẳng định rằng nếu một chuỗi hội tụ có điều kiện, có thể đổi chỗ các số hạng trong chuỗi theo một cách sao cho chuỗi hội tụ đến giá trị tùy ý, hay thậm chí là phân kỳ.
Cho
{
f
1
,
f
2
,
f
3
,
…
}
{\displaystyle \left\{f_{1},\ f_{2},\ f_{3},\dots \right\}}
∑
n
=
1
∞
f
n
{\displaystyle \sum _{n=1}^{\infty }f_{n}}
f nếu dãy các tổng riêng
{
s
n
}
{\displaystyle \{s_{n}\}}
s
n
(
x
)
=
∑
k
=
1
n
f
k
(
x
)
{\displaystyle s_{n}(x)=\sum _{k=1}^{n}f_{k}(x)}
hội tụ đều đến f .
Có một tiêu chuẩn hội tụ cho chuỗi hàm vô hạn giống với tiêu chuẩn so sánh trên, được gọi là Dấu hiệu M Weierstrass .
Tiêu chuẩn hội tụ Cauchy khẳng định rằng một chuỗi
∑
n
=
1
∞
a
n
{\displaystyle \sum _{n=1}^{\infty }a_{n}}
hội tụ khi và chỉ khi dãy tổng riêng là một dãy Cauchy . Điều này nghĩa là với mỗi
ε
>
0
,
{\displaystyle \varepsilon >0,}
N
{\displaystyle N}
n
≥
m
≥
N
{\displaystyle n\geq m\geq N}
|
∑
k
=
m
n
a
k
|
<
ε
,
{\displaystyle \left|\sum _{k=m}^{n}a_{k}\right|<\varepsilon ,}
điều này tương đương với
lim
n
→
∞
m
→
∞
∑
k
=
n
n
+
m
a
k
=
0.
{\displaystyle \lim _{n\to \infty \atop m\to \infty }\sum _{k=n}^{n+m}a_{k}=0.}





























![{\displaystyle r=\limsup _{n\rightarrow \infty }{\sqrt[{n}]{|a_{n}|}},}](https://wikimedia.org/api/rest_v1/media/math/render/svg/dd5eebb0f17b1155c0bea36edfdd50d6b9aa0f01)


















