Циклічний граф (алгебра)

В теорії груп, яка є розділом абстрактної алгебри, циклічний граф групи ілюструє різні цикли групи і особливо корисний при візуалізації структури малих скінченних груп.

Цикл — це множина ступенів даного елемента групи a, де a^n, n-та ступень елементу a визначається як добуток, помножений на себе n раз. Елемент a називається генератором циклу. У скінченній групі деяка ненульова ступінь повинна бути нейтральним елементом e; така найменша ступінь є порядком циклу, тобто кількістю різних елементів циклу. У циклічному графі, цикл зображується у вигляді багатокутника, з вершинами, що представляють елементи групи, і сполучними лініями, що вказують, на те що всі елементи в цьому багатокутнику є членами одного і того ж циклу.

Цикли

Цикли можуть частково збігатися, або вони можуть не мати жодного спільного елемента, окрім нейтрального елемента. Граф циклу відображає кожен важливий цикл у вигляді многокутника.

Якщо a породжує цикл 6-го порядку (або, більш коротко, має порядок 6), то a^6 = e. Тоді множина ступенів a^2, {a^2, a^4, e} є циклом, але це очевидно. Аналогічно, a^5 генерує той самий цикл, що і a.

Таким чином, потрібно розглядати тільки первісні цикли, а саме ті, що не є підмножинами іншого циклу. Кожен з них породжується деяким первісним елементом, a. Візьмемо вершину для кожного елемента вихідної групи. Для кожного первісного елемента, треба поєднати е і a, a вже з a^2, …, a^n−1 з a^n і т. д., поки е не буде досягнуто. В результаті отримуємо циклічний граф.

Коли a^2 = e, a має порядок 2 (це інволюція), і з'єднана з e двома ребрами. За винятком випадків, коли мета полягає в тому, щоб підкреслити, що маємо два ребра циклу, то граф, як правило, малюється[1] у вигляді однієї лінії між цими двома елементами.

Властивості

Dih4 калейдоскоп з червоним дзеркалом і 4-кратним генератором обертання

Циклічний граф для діедральної групи Dih4.

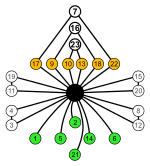
Як приклад циклічного графу групи, розглянемо діедральну групу Dih4. Таблиця множення для цієї групи показана ліворуч, а цикл графу показано праворуч із зазначенням одиничного елементу e.

^o	e	b	a	a^2	a^3	ab	a^2b	a^3b
e	e	b	a	a^2	a^3	ab	a^2b	a^3b
b	b	e	a^3b	a^2b	ab	a^3	a^2	a
a	a	ab	a^2	a^3	e	a^2b	a^3b	b
a^2	a^2	a^2b	a^3	e	a	a^3b	b	ab
a^3	a^3	a^3b	e	a	a^2	b	ab	a^2b
ab	ab	a	b	a^3b	a^2b	e	a^3	a^2
a^2b	a^2b	a^2	ab	b	a^3b	a	e	a^3
a^3b	a^3b	a^3	a^2b	ab	b	a^2	a	e

Зверніть увагу на цикл e, a, a^2, a^3. З таблиці множення можна побачити, що послідовні ступені поводяться так і у прямому, і у зворотньому порядку. Іншими словами: (a^3)^2=a^2, (a^3)^3=a, і (a^3)^4=e. Така поведінка справедлива для будь-якого циклу в будь-якій групі — цикл може бути пройдений в будь-якому напрямку.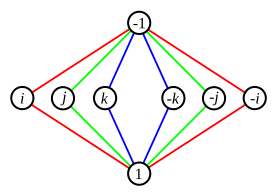

Циклічний граф групи кватерніона Q₈.

Цикли, які містять складене число елементів неявно містять цикли, які не показані в графі. Для графу Dih4 вище, ми могли б провести грань між a^2 і e, так як (a^2)^2=e, але через те, що a^2 є частиною більшого циклу, цього не можна зробити.

Існує поняття неоднозначності, коли два цикли мають спільний, не одиничний елемент. Розглянемо, наприклад, просту групу кватерніона, чий циклічний граф показаний праворуч. Кожен з елементів в середньому рядку при множенні на себе дає -1 (де 1 — це одиничний елемент). У цьому випадку ми можемо використовувати різні кольори для відстеження циклів. Як зазначалося раніше, два ребра 2-елементного циклу, як правило, представлені у вигляді одного рядка.

Обернений елемент можна знайти на циклічному графі у подібний спосіб. Це буде елемент, для якого відстань від одиничного елемента така сама, якщо рухатись по циклу у протилежному напрямку.

Історія

Циклічні графи досліджував числовий теоретик Даніель Шенкс^[en] на початку 1950-х років, як інструмент для вивчення мультиплікативних груп кільця лишків за модулем n.[2] Шенкс вперше опублікував цю ідею в 1962 у першому виданні своєї книги «Вирішені та невирішені проблеми в теорії чисел». [3] У книзі, Шенкс досліджує, які групи мають ізоморфні циклічні графи і, коли цикл є планарним графом.[4] У другому виданні 1978 року, Шенкс розмірковує про своє дослідження класових груп і розвиток алгоритму великих і малих кроків^[ru]:[5]

Графи циклу виявилися корисними при роботі з кінцевими Абелевими групами; і я використовую їх часто в пошуку шлях навколо складної структури[77, p. 852], в отриманні розшукуваного мультиплікативного співвідношення [78, с. 426], або у виділенні певної розшукуваної підгрупи [79].

Графи циклу використовуються як педагогічний інструмент у підручнику Теорія візуальних груп Натана Картера.[6]

Графи циклів деяких сімейств групи

Певні типи груп дають типові графи:

Циклічні групи Z_n, порядку n, являють собою один цикл графу простого n-кутника з вершинами елементів.

Z1	Z2 = Dih1	Z3	Z4	Z5	Z6=Z3×Z2	Z7	Z8
Z9	Z10=Z5×Z2	Z11	Z12=Z4×Z3	Z13	Z14=Z7×Z2	Z15=Z5×Z3	Z16
Z17	Z18=Z9×Z2	Z19	Z20=Z5×Z4	Z21=Z7×Z3	Z22=Z11×Z2	Z23	Z24=Z8×Z3

Z2	Z2^2 = Dih2	Z2^3 = Dih2×Dih1	Z2^4 = Dih2^2

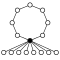
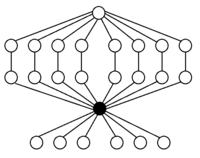
При простому числі n, групи виду (Z_n)^m матимуть (n^m − 1)/(n − 1) n-цикли, що ділять окремий елемент.

Z2^2 = Dih2	Z2^3 = Dih2×Dih1	Z2^4 = Dih2^2	Z3^2

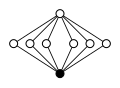
Діедральні групи Dih_n, порядку 2n складаються з циклу n-елементу і n циклів 2-елементу.

Dih1 = Z2	Dih2 = Z2^2	Dih3	Dih4	Dih5	Dih6=Dih3×Z2	Dih7	Dih8	Dih9	Dih10=Dih5×Z2

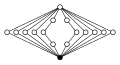
Біциклічні групи^[en], Dic_n = Q_4n, порядку 4n.

Dic2 = Q8	Dic3 = Q12	Dic4 = Q16	Dic5 = Q20	Dic6 = Q24

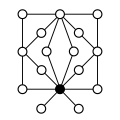
Інші прямі добутки:

Z4×Z2	Z4×Z2^2	Z6×Z2	Z8×Z2	Z4^2

Симетрична група — симетрична група S_n містить для будь-якої групи порядку n, підгрупу, ізоморфну цій групі. Таким чином, циклічний граф кожної групи порядку n можна знайти в циклічному графі S_n.

A4×Z2

S3 = Dih3

S4

Один з трьох Dih4, що знаходиться в S4 Те ж саме, що й

Див. також

• Граф Келі

Посилання

• Weisstein, Eric W. Cycle Graph(англ.) на сайті Wolfram MathWorld.
• R. J. Mathar (2014). Plots of cycle graphs of the finite groups up to order 36.

Примітки

1. Sarah Perkins (2000). Commuting Involution Graphs for A˜n, Section 2.2, p.3, first figure (PDF). Birkbeck College, Malet Street, London, WC1E 7HX: School of Economics, Mathematics and Statistics. Процитовано 31 січня 2016.
2. Shanks, 1978, с. 246.
3. Shanks, 1978, с. xii.
4. Shanks, 1978, с. 83—98, 206—208.
5. Shanks, 1978, с. 225.
6. Carter, Nathan (2009), Visual Group Theory, Classroom Resource Materials, Mathematical Association of America, ISBN 978-0-88385-757-1

• Skiena, S. Implementing Discrete Mathematics: Combinatorics and Graph Theory with Mathematica 1990, § 4.2.3 Cycles, Stars, and Wheels, pp. 144—147
• Shanks, Daniel (1978) [1962], Solved and Unsolved Problems in Number Theory (вид. 2nd), New York: Chelsea Publishing Company, ISBN 0-8284-0297-3
• Pemmaraju, S. and Skiena, S. Computational Discrete Mathematics: Combinatorics and Graph Theory in Mathematics Cambridge, England: Cambridge University Press, 2003, § 6.2.4 Cycles, Stars, and Wheels pp. 248—249