Категорія коми

У теорії категорій, категорія коми — спеціальна конструкція, що надає спосіб вивчення морфізмів не як співвіднесення об'єктів категорії один з одним, а як самостійних об'єктів. Назва «категорія коми» з'явилася через початкове (введене Ловером^[en]) позначення, яке включало знак коми. Згодом стандартне позначення змінилося з міркувань зручності.

Визначення

Загальний випадок

Нехай ${\displaystyle {\mathcal {A}},{\mathcal {B}}}$ і ${\displaystyle {\mathcal {C}}}$ — категорії, а ${\displaystyle S}$ і ${\displaystyle T}$ — функтори

${\displaystyle {\mathcal {A}}{\xrightarrow {\;\;S\;\;}}{\mathcal {C}}{\xleftarrow {\;\;T\;\;}}{\mathcal {B}}}$

Категорію коми ${\displaystyle (S\downarrow T)}$ можна побудувати так:

• Об'єкти — всі трійки вигляду ${\displaystyle (\alpha ,\beta ,f)}$, де ${\displaystyle \alpha }$ — об'єкт ${\displaystyle {\mathcal {A}}}$, ${\displaystyle \beta }$ — Об'єкт ${\displaystyle {\mathcal {B}}}$, і ${\displaystyle f:S(\alpha )\rightarrow T(\beta )}$ — морфізм у ${\displaystyle {\mathcal {C}}}$.
• Морфізм з ${\displaystyle (\alpha ,\beta ,f)}$ в ${\displaystyle (\alpha ',\beta ',f')}$ — всі пари ${\displaystyle (g,h)}$, де ${\displaystyle g:\alpha \rightarrow \alpha '}$, ${\displaystyle h:\beta \rightarrow \beta '}$ — морфізми в ${\displaystyle {\mathcal {A}}}$ і ${\displaystyle {\mathcal {B}}}$ відповідно, такі, що комутує така діаграма:

${\displaystyle {\begin{matrix}S(\alpha )&{\xrightarrow {S(g)}}&S(\alpha ')\\f{\Bigg \downarrow }&&{\Bigg \downarrow }f'\\T(\beta )&{\xrightarrow[{T(h)}]{}}&T(\beta ')\end{matrix}}}$

Якщо останній вираз визначено, композиція морфізмів ${\displaystyle (g,h)\circ (g',h')}$ береться як ${\displaystyle (g\circ g',h\circ h')}$. Тотожний морфізм об'єкта ${\displaystyle (\alpha ,\beta ,f)}$ — це ${\displaystyle (\mathrm {id} _{\alpha },\mathrm {id} _{\beta })}$.

Два часткових випадки

Розглянемо два часткових випадки, які простіші й трапляються дуже часто.

Перший випадок — категорія об'єктів над ${\displaystyle A}$. Нехай у попередньому визначенні ${\displaystyle {\mathcal {A}}={\mathcal {C}}}$, ${\displaystyle S}$ — тотожний функтор і ${\displaystyle {\mathcal {B}}={\textbf {1}}}$ (категорія з одним об'єктом ${\displaystyle *}$ та одним морфізмом). Тоді ${\displaystyle T(*)=A}$ для деякого об'єкта ${\displaystyle A}$ категорії ${\displaystyle {\mathcal {C}}}$. У цьому випадку використовують позначення ${\displaystyle ({\mathcal {C}}\downarrow A)}$. Об'єкти вигляду ${\displaystyle (\alpha ,*,f)}$ — це просто пари ${\displaystyle (\alpha ,f)}$, де ${\displaystyle f:\alpha \rightarrow A}$. Іноді в цій ситуації ${\displaystyle f}$ позначають як ${\displaystyle \pi _{\alpha }}$. Морфізм з ${\displaystyle (B,\pi _{B})}$ в ${\displaystyle (B',\pi _{B'})}$ — це морфізм ${\displaystyle g:B\rightarrow B'}$, що замикає до комутативної таку діаграму:

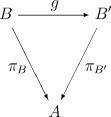
Двоїстий випадок — категорія об'єктів під ${\displaystyle A}$. Тут ${\displaystyle S}$ — функтор з 1 і ${\displaystyle T}$ — тотожний функтор. У цьому випадку використовують позначення ${\displaystyle (A\downarrow {\mathcal {C}})}$, де ${\displaystyle A}$ — об'єкт ${\displaystyle {\mathcal {C}}}$, в який відображає ${\displaystyle S}$. Об'єкти — пари ${\displaystyle (B,i_{B})}$, де ${\displaystyle i_{B}:A\rightarrow B}$. Морфізм між ${\displaystyle (B,i_{B})}$ і ${\displaystyle (B',i_{B'})}$ — відображення ${\displaystyle h:B\rightarrow B'}$, що замикає до комутативної таку діаграму:

Категорія стрілок

Ще один частковий випадок — коли ${\displaystyle S}$ і ${\displaystyle T}$ — тотожні функтори в ${\displaystyle {\mathcal {C}}}$ (так що ${\displaystyle {\mathcal {A}}={\mathcal {B}}={\mathcal {C}}}$). У цьому випадку категорію коми називають категорією стрілок ${\displaystyle {\mathcal {C}}^{\rightarrow }}$. Її об'єкти — морфізми ${\displaystyle {\mathcal {C}}}$, а її морфізми — комутативні квадрати в ${\displaystyle {\mathcal {C}}}$[1].

Властивості

Для будь-якої категорії стрілок визначено два забутливі функтори з неї:

• Функтор прообразу ${\displaystyle S\downarrow T\to {\mathcal {A}}}$, який відображає:
  • об'єкти: ${\displaystyle (\alpha ,\beta ,f)\mapsto \alpha }$;
  • морфізми: ${\displaystyle (g,h)\mapsto g}$;
• Функтор образу, ${\displaystyle S\downarrow T\to {\mathcal {B}}}$, який відображає:
  • об'єкти: ${\displaystyle (\alpha ,\beta ,f)\mapsto \beta }$;
  • морфізми: ${\displaystyle (g,h)\mapsto h}$.

Приклади

• Категорія множин із відміченою точкою — це категорія коми ${\displaystyle (\bullet \downarrow \mathbf {Set} )}$, де ${\displaystyle \bullet }$ — функтор, що вибирає деякий синґлетон, і ${\displaystyle \mathbf {Set} }$ — Тотожний функтор у категорії множин. У подібний спосіб можна утворити категорію топологічних просторів із зазначеною точкою ${\displaystyle (\bullet \downarrow \mathbf {Top} )}$.
• Категорія графів — це категорія коми ${\displaystyle (\mathbf {Set} \downarrow D)}$, де ${\displaystyle D:\mathbf {Set} \rightarrow \mathbf {Set} }$ — функтор, що відправляє ${\displaystyle s}$ в ${\displaystyle s\times s}$. Об'єкти вигляду ${\displaystyle (a,b,f)}$ складаються з двох множин та функції; ${\displaystyle a}$ — індексує множину для ребер, ${\displaystyle b}$ — множину вершин, тоді ${\displaystyle f:a\rightarrow (b\times b)}$ вибирає пару елементів ${\displaystyle b}$ для кожного ${\displaystyle a}$, тобто ${\displaystyle f}$ вибирає певне ребро зі множини можливих ребер ${\displaystyle b\times b}$. Морфізми в цій категорії — функції індексувальній множині і множині вершин, такі, що образи вершин, які відповідали даному ребру, відповідатимуть його образу.

Спряження

Функтори ${\displaystyle F:{\mathcal {C}}\rightarrow {\mathcal {D}}}$ і ${\displaystyle G:{\mathcal {D}}\rightarrow {\mathcal {C}}}$ спряжені тоді й лише тоді, коли категорії коми ${\displaystyle (F\downarrow id_{\mathcal {D}})}$ і ${\displaystyle (id_{\mathcal {C}}\downarrow G)}$ ізоморфні, причому еквівалентні елементи проєктуються на той самий елемент ${\displaystyle {\mathcal {C}}\times {\mathcal {D}}}$. Це дозволяє описати сполучені функтори, не використовуючи множини, і це було головною причиною появи конструкції категорій коми.

Природні перетворення

Якщо образи ${\displaystyle S,T}$ збігаються, то діаграма, що визначає морфізм у ${\displaystyle S\downarrow T}$ з ${\displaystyle \alpha =\beta ,\alpha '=\beta ',g=h}$ збігається з діаграмою, що визначає натуральне перетворення ${\displaystyle S\to T}$. Відмінність між двома визначеннями полягає в тому, що натуральне перетворення — це певний клас морфізмів вигляду ${\displaystyle S(\alpha )\to T(\alpha )}$, тоді як об'єкти категорії коми — це все морфізми такого вигляду. Функтор у категорію коми може вибрати конкретне сімейство морфізмів. І справді, натуральному перетворенню ${\displaystyle \eta :S\to T}$, де ${\displaystyle S,T:{\mathcal {A}}\to {\mathcal {C}}}$ відповідає функтор ${\displaystyle {\mathcal {A}}\to (S\downarrow T)}$, який відображає об'єкт ${\displaystyle \alpha }$ в ${\displaystyle (\alpha ,\alpha ,\eta _{\alpha })}$ і морфізми ${\displaystyle g}$ в ${\displaystyle (g,g)}$. Це задає бієкцію між природними перетвореннями ${\displaystyle S\to T}$ та функторами ${\displaystyle {\mathcal {A}}\to (S\downarrow T)}$, які є лівими оберненими обох забутливих функторів з ${\displaystyle S\downarrow T}$.

Примітки

1. Adámek, Jiří; Horst Herrlich, and George E. Strecker. Abstract and Concrete Categories. — John Wiley & Sons, 1990. — ISBN 0-471-60922-6. Архівовано з джерела 21 квітня 2015

Література

• С. Маклейн Категории для работающего математика, — М.: ФИЗМАТЛИТ, 2004. — 352 с. — ISBN 5-9221-0400-4.