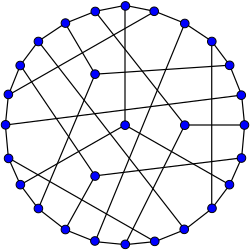
Граф Коксетера

Граф Коксетера
Вершин	28
Ребер	42
Радіус	4
Діаметр	4
Обхват	7
Автоморфізм	336 (ПЛГ2(7))
Хроматичне число	3
Хроматичний індекс	3
Число черг	2
Властивості	симетричний кубічний дистанційно-регулярний дистанційно-транзитивний гіпогамільтонів^[en]

Граф Коксетера — 3-регулярний граф з 28 вершинами і 42 ребрах[1]. Усі кубічні дистанційно-регулярні графи відомі[2], граф Коксетера — один з 13-ти таких графів.

Властивості

Хроматичне число графа 3, хроматичний індекс дорівнює 3, радіус дорівнює 4, діаметр — 4 обхват — 7. Граф є також вершинно 3-зв'язним і реберно 3-зв'язним.

Граф Коксетера є гіпогамільтонівським графом — сам по собі він не містить гамільтонових циклів, але видалення будь-якої вершини робить його гамільтоновим. Число прямолінійних схрещень графа Коксетера дорівнює 11 і це мінімальний відомий кубічний граф з таким числом схрещень, хоча графи з 26 вершинами і числом схрещень 11 існувати можуть[3].

Граф Коксетера можна побудувати з меншого дистанційно-регулярного графа Хівуда шляхом створення вершини для кожного 6-циклу в графі Хивуда і ребра для кожної незв'язної пари 6-циклів.[4]

Граф Коксетера також можна отримати з графа Гофмана — Синглтона. Візьмемо будь яку вершину v графа Гофмана — Синглтона. Існує незалежна множина розміру 15, яка містить v. Видалимо 6 сусідів v і цю незалежну множину, включаючи v залишимо.

Алгебраїчні властивості

Група автоморфізмів графа Коксетера — це група порядку 336[5]. Вона діє транзитивно на вершини і ребра графа, тому граф Коксетера є симетричним. Граф має автоморфизми, які переводять будь-яку вершину в будь-яку іншу і будь-яке ребро будь-яке інше ребро. У «списку Фостера» граф Коксетера, зазначений як F28A, є єдиним кубічним симетричним графом з 28 вершинами[6].

Граф Коксетера однозначно визначається за його спектром, тобто множиною власних значень матриці суміжності графа[7].

Як скінченно зв'язний вершинно-транзитивний граф, що не містить гамільтонових циклів, граф Коксетера є контрприкладом варіанту гіпотези Ловаса, але канонічна формулювання гіпотези вимагає наявності гамільтонового циклу.

Відомо лише п'ять вершинно-транзитивних графів без гамільтонових циклів — повний граф «K»₂, граф Петерсена, граф Коксетера і два графи, отримані з графів Петерсена і Коксетера шляхом заміни кожної вершини трикутником[8].

Характеристичний поліном графа Коксетера дорівнює ${\displaystyle (x-3)(x-2)^{8}(x+1)^{7}(x^{2}+2x-1)^{6}}$. Граф є єдиним графом з таким поліномом, що і дозволяє однозначно визначити граф Коксетера за його спектром.

Галерея

• 
  Граф, отриманий видаленням будь-якого ребра з графа Коксетера є гамільтоново-зв'язним.
• 
  Хроматичне число графа Коксетера дорівнює 3.
• 
  Число прямолінійних схрещень графа Коксетера дорівнює 11.

Примітки

1. Weisstein, Eric W. Coxeter Graph(англ.) на сайті Wolfram MathWorld.
2. A. E. Брауер, A. M. Cohen, A. Neumaier. Distance-Regular Graphs. — New York : Springer-Verlag, 1989. (англ.)
3. послідовність A110507 з Онлайн енциклопедії послідовностей цілих чисел, OEIS
4. Italo J. Dejter. From the Coxeter graph to the graph Klein // Journal of теорія Графів. — 2011. — arXiv:1002.1960. — DOI:10.1002/jgt.20597..
5. Royle, G. F028A data^[недоступне посилання з квітня 2019]
6. M. Conder, P. Dobcsányi, «Trivalent Symmetric Graphs Up to 768 Vertices.» J. Combin. Math. Combin. Comput. 40, 41-63, 2002.
7. E. R. van Dam and W. H. Haemers, Spectral Characterizations of Some Distance-Regular Graphs. J. Алгебраїчна Combin. 15, pages 189—202, 2003
8. Royle, G. «Cubic Symmetric Graphs (Foster The Census).» [Архівовано 20 липня 2008 у Wayback Machine.]