|
Індукція назадІндукція назад, індукція з кінця або обернена індукція — це процес міркування обернений у часі, від кінця задачі або ситуації, щоб визначити послідовність найсприятливіших дій. Він рухається розглядаючи останню точку, в якій треба ухвалювати рішення і тоді з'ясовує яка дія буде найоптимальнішою в цю мить. Послуговуючись цими даними, ви можете визначити, що робити під час ухвалення другого з кінця рішення. Цей процес триває назад в часі допоки не буде визначено найліпші дії для всіх можливих становищ (наприклад, для кожної можливої інформаційної множини[en]) у кожну точку в часі. Індукцію назад вперше в 1875 році ужив Артур Кейлі, який відкрив метод намагаючись розв'язати горезвісну задачу про перебірливу наречену.[1] У математичній оптимізації оптимізації в методі динамічного програмування індукція назад це один з головних підходів для розв'язання рівняння Беллмана.[2][3] У теорії ігор, індукція назад це метод використовуваний для обчислення досконалої рівноваги підігор[en] у послідовних іграх.[4] Єдина різниця це те, що оптимізація залучає лише одного ухвалювача рішень, який обирає, що робити кожної миті, тоді як теорія ігор аналізує як взаємодіють рішення кількох гравців. Тобто передбачаючи, що останній гравець робитиме в кожній ситуації, ми можемо визначити, що робитиме другий з кінця гравець і так далі. У пов'язаних галузях автоматизованого планування та диспетчеризації й автоматизованого доведення теорем, метод називається пошуком назад або зворотним виводом. У шахах він відомий як ретроспективний аналіз. Індукцію назад використовували для розв'язання ігор так довго як довго існувала теорія ігор. Джон фон Нейман і Оскар Морґенштерн запропонували розв'язувати ігри з нульовою сумою і двома гравцями за допомогою індукції назад у їхній книжці Теорія ігор і економічної поведінки (1944), ця книжка вводила теорію ігор як напрямок для дослідження.[5][6] Індукція назад в ухвалені рішень: задача оптимальної зупинкиРозгляньмо безробітну людину, яка зможе працювати ще десять років t = 1,2,…,10. Припустімо, що кожен рік, протягом якого вона залишається безробітною, їй можуть запропонувати «хорошу» роботу з оплатою 100 доларів або «погану» роботу з оплатою 44 долари з рівною ймовірністю (50/50). Щойно вона погодиться на роботу, вона залишатиметься на цій роботі протягом решти десяти років. (Для простоти припустимо, що вона дбає лише про свої грошові доходи, і що вона оцінює доходи в різний час однаково, тобто ставка дисконту дорівнює одиниці.) Чи повинна ця людина погоджуватися на погану роботу? Щоб відповісти на це запитання, ми можемо міркувати в зворотному напрямку від часу t = 10.
Задача динамічної оптимізації такого типу називається задачею оптимальної зупинки, бо питання полягає в тому, коли припинити очікування кращої пропозиції. Теорія пошуку[en] — це галузь мікроекономіки, яка застосовує задачі такого типу до таких контекстів, як покупки, пошук роботи та шлюб. Індукція назад в теорії ігорУ теорії ігор обернена індукція є концепцією рішення. Це уточнення концепції раціональності, яка чутлива до окремих інформаційних множин[en] в екстенсивному представленні гри.[7] Ідея оберненої індукції використовує послідовну раціональність шляхом визначення оптимальної дії для кожної інформації в даному дереві гри. У «Стратегії: Вступ до теорії ігор» Джоела Уотсона процедура зворотної індукції визначається як: «Процес аналізу гри від кінця до початку. На кожному вузлі прийняття рішень вилучаються з розгляду будь-які дії, які є домінуючими, враховуючи термінальні вузли, які можуть бути досягнуті через гру дій, визначених на наступних вузлах».[8] Одним із недоліків процедури зворотної індукції є те, що її можна застосовувати лише до обмежених класів ігор. Процедура чітко визначена для будь-якої гри з досконалою інформацією без прив'язки до користі. Вона також чітко визначена й значуща для ігор ідеальної інформації зі зв'язками. Однак це призводить до понад одного профілю стратегії. Процедуру можна застосувати до деяких ігор з нетривіальними інформаційними множинами, але в цілому вона ненадійна. Процедура найкраще підходить для розв'язування ігор з ідеальною інформацією. Тому, якщо всі гравці не усвідомлюють дії інших гравців і виграші на кожному вузлі від прийняття рішень, тоді обернену індукцію не так легко застосувати. (Ватсон с. 188)[9] Процедуру зворотної індукції можна продемонструвати на простому прикладі. Багатоетапна граРозгляньмо багатоетапну гру[en], в якій беруть участь 2 гравці. Гравці планують піти в кіно. Зараз є 2 фільми, які дуже популярні, Джокер і Термінатор. Гравець 1 хоче дивитися Термінатора, а Гравець 2 хоче дивитися Джокера. Гравець 1 першим купить квиток і повідомить Гравцю 2 про свій вибір. Тоді Гравець 2 купить свій квиток. Після того як вони обидва спостерігатимуть за вибором, вони вирішать, піти їм у кіно чи залишитися вдома. Як і на першому етапі, гравець 1 обирає першим. Потім гравець 2 робить свій вибір після спостереження за вибором гравця 1. У цьому прикладі ми припускаємо, що виграш додається на різних етапах. Гра є грою з повною інформацією. Матриця нормальної форми:
Розгорнута форма[en] гри Джокер/Термінатор: Кроки для розв'язання цієї багатоетапної гри з великою формою, як показано праворуч: 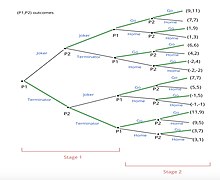
Гра в ультиматумІндукція назад — це «процес аналізу гри від кінця до початку». Як і при розв'язуванні інших рівноваг Неша, передбачається раціональність гравців і повне знання. Концепція оберненої індукції відповідає цьому припущенню, бо загальновідомо, що кожен гравець діятиме раціонально з кожним вузлом ухвалення рішень, коли він обирає варіант — навіть якщо його раціональність означатиме, що такий вузол не буде досягнутий».[11] Отже, за умови взаємного припущення раціональності, індукція назад дозволяє кожному гравцеві точно передбачити, що буде робити його суперник на кожному етапі гри. Щоб розв'язати досконалу за підіграми рівновагу[en] за допомогою оберненою індукції, гру слід записати в розгорнутій формі, а потім розділити на підігри. Починаючи з підгри найдальшої від початкового вузла або початкової точки, очікувані виграші, зазначені для цієї підгри, зважуються, і раціональний гравець вибере для себе варіант із вищою віддачею. Вибирається та позначається вектор найбільшого виграшу. Знайдіть ідеальну рівновагу в підгрі, постійно працюючи назад від підгри до підгри, поки не досягнете початкової точки. У міру того, як цей процес просувається, ваша початкова гра в екстенсивній формі ставатиме все коротшою. Цей позначений шлях векторів є ідеальною рівновагою підгри.[1] Індукція назад, застосована до гри в ультиматумПодумайте про гру між двома гравцями, де гравець 1 пропонує розділити один долар з гравцем 2. Це відома асиметрична гра, у яку грають послідовно і називають грою «ультиматум»[en]. Перший гравець діє першим, розділяючи долар так, як вважає за потрібне. Тепер другий гравець може прийняти частину, яку йому роздав перший гравець, або відмовитися від розподілу. Якщо гравець 2 приймає розподіл, то гравець 1 і гравець 2 отримують виграш відповідно до цього розподілу. Якщо другий гравець вирішить відхилити пропозицію гравця 1, обидва гравці нічого не отримають. Іншими словами, гравець 2 має право вето на запропонований розподіл гравця 1, але застосування вето усуває будь-яку винагороду для обох гравців.[12] Таким чином, профіль стратегії для цієї гри можна записати у вигляді пар (x, f(x)) для всіх x від 0 до 1, де f(x)) є двозначною функцією, яка виражає, приймається x чи ні. Розгляньмо вибір і відповідь гравця 2 на будь-яку довільну пропозицію гравця 1, припускаючи, що пропозиція перевищує 0 доларів. Використовуючи обернену індукцію, безсумнівно, ми очікуємо, що гравець 2 прийме будь-яку виграш, що перевищує або дорівнює 0 доларів. Відповідно, гравець 1 повинен запропонувати дати гравцеві 2 якомога менше, щоб отримати найбільшу частину розподілу. Якщо гравець 1 дає гравцеві 2 найменшу грошову одиницю, а решту залишає собі, це унікальна ідеальна рівновага в підгрі. Гра «Ультиматум» має кілька інших рівноваг Неша, які не є ідеальними підіграми і тому не потребують індукції назад. Гра в ультиматум це ілюстрація корисності оберненої індукції при розгляді нескінченних ігор; однак теоретично передбачені результати гри піддаються критиці. Емпіричні експериментальні дані показали, що пропонент дуже рідко пропонує 0 доларів, а гравець 2 іноді навіть відхиляє пропозиції, що перевищують 0 доларів, мабуть, з міркувань справедливості. Те, що гравець 2 вважає справедливим, залежить від контексту, і тиск або присутність інших гравців може означати, що теоретична модель ігор не обов'язково може передбачити, що виберуть реальні люди. На практиці ідеальна рівновага в підгрі не завжди досягається. За словами Камерера, американського поведінкового економіста, гравець 2 «відхиляє пропозиції менш ніж на 20 відсотків від X приблизно в половині випадків, навіть якщо в кінцевому підсумку він не отримує нічого».[13] Хоча індукція назад передбачила б, що респондент приймає будь-яку пропозицію рівну або більшу нуля, респонденти насправді не раціональні гравці і тому, здається, більше піклуються про «справедливість» пропозиції, а не про потенційні грошові вигоди. Дивіться також гру «стонога». Обернена індукція в економіці: ухвалення рішення про вхід на ринокРозгляньмо динамічну гру, в якій гравцями є фірма, що посідає усталену позицію в галузі, й потенційний новий учасник цієї галузі. У поточному стані усталений оператор має монополію на галузь і не хоче втрачати частину своєї частки ринку на користь нового. Якщо учасник вирішує не вступати, виграш для чинного учасника є високим (він зберігає свою монополію), і учасник не втрачає і не отримує (його виграш дорівнює нулю). Якщо новачок вступає, то усталений може «воювати» або «примиритись» з новачком. Він може боротися, знижуючи свою ціну, виводячи конкурента з бізнесу (і несучи витрати на виході — від'ємний виграш) і завдаючи шкоди власним прибуткам. Якщо він піде назустріч учаснику, він втратить частину своїх продажів, але висока ціна збережеться, і він отримає більший прибуток, ніж від зниження ціни (але нижчий, ніж прибуток монополії). Подумайте, чи найкращою відповіддю посадової особи є примирення, якщо вступає новачок. Якщо чинний оператор погоджується, найкраща відповідь учасника — увійти (і отримати прибуток). Таким чином, стратегічний профіль, до якого вступає новачок, і усталений оператор примиряється, якщо новий вступає, є рівновагою Неша, що відповідає оберненій індукції. Проте, якщо усталений учасник збирається битися, найкраща відповідь учасника — не вступати, і якщо учасник не вступає, не має значення, що він вирішить робити в гіпотетичному випадку, коли учасник все ж вступить. Таким чином, стратегічний профіль, у якому усталений учасник бореться, якщо вступає учасник, але учасник не вступає, також є рівновагою Неша. Однак, якщо учасник відхилиться і увійде, найкращою реакцією усталеного учасника буде примирення — загроза бійки не викликає довіри. Тому цю другу рівновагу Неша можна усунути за допомогою оберненої індукції. Знаходження рівноваги Неша в кожному процесі ухвалення рішень (підгрі) є ідеальною підігровою рівновагою. Таким чином, ці профілі стратегії, які зображують ідеальну рівновагу підігор, виключають можливість таких дій, як неймовірні загрози, які використовуються, щоб «відлякати» нового учасника. Якщо діючий оператор погрожує розпочати війну цін з новим учасником, він погрожує знизити свої ціни з монопольної ціни до трохи нижчої, ніж у нового учасника, що було б непрактично та неймовірно, якби учасник знав, що цінової війни насправді не буде, бо це призведе до втрат для обох сторін. На відміну від оптимізації за допомогою одного агента, яка включає в себе рівноваги, які є нездійсненними або оптимальними, ідеальна рівновага підгри враховує дії іншого гравця, таким чином гарантуючи, що жоден гравець не досягне підгри помилково. У цьому випадку обернена індукція, яка дає ідеальну рівновагу підігор, гарантує, що учасник не буде переконаний у загрозі чинного гравця, знаючи, що це була не найкраща відповідь у профілі стратегії.[14] Парадокс індукції назад: раптова стратаПарадокс раптової страти — це парадокс, пов'язаний з оберненою індукцією. Припустімо, що ув'язненій сказали, що її повісять десь між понеділком і п'ятницею наступного тижня. Однак точний день не відомий (тобто, вона не знатиме напередодні ввечері, що наступного дня її стратять). Ув'язнена, зацікавлена в тому, щоб перехитрити свого ката, намагається визначити, в який день відбудеться страта. Вона вважає, що це не може відбутися в п'ятницю, бо якби це не відбулося до кінця четверга, вона б знала, що страта буде в п'ятницю. Тому вона може виключити п'ятницю як можливість. Коли п'ятницю вилучено, вона вирішує, що це не може відбутися в четвер, бо якби це не відбулося в середу, вона знала б, що це мало бути в четвер. Тому вона може усунути четвер. Це міркування триває, доки вона не усуне всі можливості. Вона робить висновок, що наступного тижня її не повісять. На її подив, у середу її вішають. Вона зробила помилку, припустивши, що вона точно знала, чи невідомий майбутній чинник, який спричинить її страту, є тим, про який вона може міркувати. Тут ув'язнена міркує за оберненою індукцією, але, здається, доходить до помилкового висновку. Зауважте, однак, що опис задачі передбачає можливість здивувати когось, хто виконує індукцію назад. Математична теорія оберненої індукції не робить цього припущення, тому парадокс не ставить під сумнів висліди цієї теорії. Тим не менш, цей парадокс викликав серйозні дискусії серед філософів. Обернена індукція та загальні знання про раціональністьЗворотна індукція працює, лише якщо обидва гравці раціональні, тобто завжди обирають дію, яка максимізує їхній виграш. Однак раціональності недостатньо: кожен гравець також повинен вірити, що всі інші гравці є раціональними. Навіть цього недостатньо: кожен гравець повинен вірити, що всі інші гравці знають, що всі інші гравці раціональні. І так до нескінченності. Іншими словами, раціональність має бути загальновідомою.[15] Обмежена індукція назадДосліди показали, що в іграх із послідовним торгом, таких як гра «Стонога», суб'єкти відхиляються від теоретичних прогнозів і замість цього беруть участь у обмеженій оберненій індукції. Це відхилення виникає як наслідок обмеженої раціональності, коли гравці можуть чітко бачити лише на кілька етапів вперед.[16] Це допускає непередбачуваність у рішеннях і недієвість у пошуку та досягненні підігрової ідеальної рівноваги Неша[en].  Існує три широкі гіпотези цього явища;
Порушення оберненої індукції переважно пояснюється наявністю соціальних чинників. Однак прогнози моделі на основі даних для послідовних ігор з угодою (з використанням моделі когнітивної ієрархії[en]) підкреслили, що в деяких іграх присутність обмеженої оберненої індукції може відігравати панівну роль.[17] У рамках повторюваних ігор суспільних благ на поведінку команди впливає обмежена обернена індукція; де очевидно, що початкові внески членів команди вищі, ніж внески ближче до кінця. Обмежена обернена індукція також впливає на те, наскільки регулярно відбувається безкоштовне користування в грі суспільних благ команди. На початку, коли вплив обмеженої зворотної індукції низький, безквитковий проїзд зустрічається рідше, тоді як ближче до кінця, коли ефект значний, безквитковий проїзд стає частішим.[18] Обмежена зворотна індукція також була перевірена на наявність у варіанті перегонової гри. У грі гравці послідовно вибирають цілі числа в діапазоні та підсумовують свій вибір, доки не буде досягнуто цільове число. Влучання в ціль приносить цьому гравцеві приз; інший програє. Під час серії ігор було введено невеликий проміжний приз. Тоді більшість гравців виконали обмежену індукцію назад, бо вони вирішили отримати невеликий приз, а не початковий приз. Лише невелика частина гравців розглядала обидва призи на початку.[19] Більшість випробувань індукції назад відбулось на дослідах, в яких учасники не заохочуються або лише незначною мірою заохочуються виконати завдання якісно. Однак порушення оберненої індукції також поширене в середовищах з високими ставками. Широкомасштабний аналіз американського телешоу «The Price Is Right», наприклад, надає докази обмеженого передбачення. У кожному епізоді учасники грають у «Showcase Showdown», послідовну гру з досконалою інформацією, для якої оптимальну стратегію можна знайти за допомогою оберненої індукції. Часті й систематичні відхилення від оптимальної поведінки свідчать про те, що значній частині учасників не вдається належним чином індукувати назад і вони короткозоро розглядають лише наступний етап гри.[20] Примітки
|