Ізопериметрична точка

У геометрії ізопериметрична точка — це особлива точка, пов'язана з плоским трикутником. Термін був спочатку введений Г. Р. Вельдкампом у статті, опублікованій в American Mathematical Monthly в 1985 році, для позначення точки P у площині трикутника ABC, яка має властивість, що трикутники PBC, PCA і PAB мають рівні периметри, тобто[1][2]

PB + BC + CP = PC + CA + AP = PA + AB + BP.

Ізопериметричні точки в розумінні Вельдкампа існують лише для трикутників, які задовольняють певним умовам. Ізопериметрична точка трикутника ABC у розумінні Вельдкампа, якщо вона існує, має такі трилінійні координати:[3]

(sec (A/2) cos (B/2) cos (C/2) − 1 , sec (B/2) cos (C/2) cos (A/2) − 1 , sec (C/2) cos (A/2) cos (B/2) − 1)

Для будь-якого трикутника ABC можна пов'язати з ним точку P, що має трилінійні координати, як зазначено вище. Ця точка є чудовою точкою трикутника, і в Енциклопедії центрів трикутника Кларка Кімберлінга (ETC) вона називається ізопериметричною точкою трикутника ABC. Її позначають як центр трикутника X(175).[4] Точка X(175) не обов'язково є ізопериметричною точкою трикутника ABC у сенсі Вельдкампа. Проте, якщо існує ізопериметрична точка трикутника ABC у розумінні Вельдкампа, то вона буде тотожною точці X(175). Точка P з властивістю трикутників PBC, PCA і PAB мати рівні периметри була досліджена ще в 1890 році в статті Еміля Лемуана.[4][5]

Існування ізопериметричної точки в розумінні Вельдкампа

Трикутник ABC, в якому чудова точка X(175) не є ізопериметричною точкою в розумінні Вельдкампа.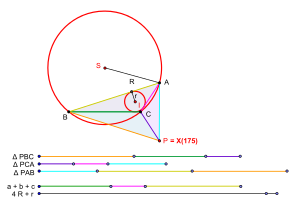

Нехай ABC — довільний трикутник, довжини його сторін дорівнюють a, b і c, радіус описаного кола дорівнює R, а радіус вписаного кола — r. Необхідну і достатню умову існування ізопериметричної точки в розумінні Вельдкампа можна сформулювати так.[1]

Трикутник ABC має ізопериметричну точку в розумінні Вельдкампа тоді і тільки тоді, коли a + b + c > 4R + r .

Для всіх гострокутних трикутників ABC маємо a + b + c > 4R + r, тому всі гострокутні трикутники мають ізопериметричну точку в розумінні Вельдкампа.

Властивості

Нехай P — чудова точка трикутника X(175) трикутника ABC.[4] Тоді:

• P лежить на прямій, що з'єднує центр вписаного кола і точку Жергона трикутника ABC.
• Якщо P — ізопериметрична точка трикутника ABC у розумінні Вельдкампа, то зовнівписані кола трикутників PBC, PCA, PAB попарно дотикаються одна до одної, а P — їхній радикальний центр.
• Якщо P — ізопериметрична точка трикутника ABC у розумінні Вельдкампа, то периметри трикутників PBC, PCA, PAB дорівнюють 2 Δ / |4 R + r — (a + b + c)|, де Δ — площа, R — радіус описаного кола, r — радіус вписаного кола, a, b, c — довжини сторін трикутника ABC.[6]

Кола Содді

Внутрішнє і зовнішнє кола Содді у випадку, коли зовнішня точка Содді є ізопериметричною точкою у розумінні Вельдкампа.

Внутрішні та зовнішні кола Содді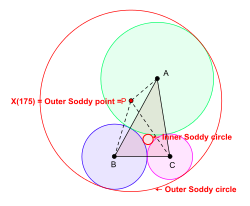 у випадку, коли зовнішня точка Содді не є ізопериметричною точкою у розумінні Вельдкампа.

Для даного трикутника ABC можна накреслити кола в площині трикутника ABC з центрами в точках A, B і C так, щоб вони дотикалися один до одного зовні. Загалом, можна намалювати два нових кола, кожне з яких буде дотичним до трьох кіл з центрами A, B, C. (Одне з кіл може виродитися в пряму лінію.) Ці кола називають колами Содді трикутника ABC. Коло з меншим радіусом є внутрішнім колом Содді, а його центр називається внутрішньою точкою Содді або внутрішнім центром Содді трикутника ABC. Коло з більшим радіусом є зовнішнім колом Содді, а його центр називається зовнішньою точкою Содді або зовнішнім центром Содді трикутника ABC.[6][7] Чудова точка трикутника X(175), ізопериметрична точка в розумінні Кімберлінга, є зовнішньою точкою Содді трикутника ABC.

Примітки

1. G. R. Veldkamp (1985). The isoperimetric point and the point(s) of equal detour. Amer. Math. Monthly. 92 (8): 546—558. doi:10.2307/2323159. JSTOR 2323159.
2. Hajja, Mowaffaq; Yff, Peter (2007). The isoperimetric point and the point(s) of equal detour in a triangle. Journal of Geometry. 87 (1–2): 76—82. doi:10.1007/s00022-007-1906-y.
3. Kimberling, Clark. Isoperimetric Point and Equal Detour Point. Архів оригіналу за 10 травня 2012. Процитовано 27 травня 2012.
4. Kimberling, Clark. X(175) Isoperimetric Point. Архів оригіналу за 19 квітня 2012. Процитовано 27 травня 2012.
5. The article by Emile Lemoine can be accessed in Gallica. The paper begins at page 111 and the point is discussed in page 126.Gallica [Архівовано 28 грудня 2021 у Wayback Machine.]
6. Nikolaos Dergiades (2007). The Soddy Circles (PDF). Forum Geometricorum. 7: 191—197. Архів оригіналу (PDF) за 14 червня 2010. Процитовано 29 травня 2012. [Архівовано 2010-06-14 у Wayback Machine.]
7. Soddy Circles. Архів оригіналу за 4 березня 2016. Процитовано 29 травня 2012.

Посилання

• isoperimetric and equal detour points [Архівовано 28 грудня 2021 у Wayback Machine.] — інтерактивна ілюстрація на Geogebratube