กฎของแก๊สอุดมคติ

เส้นอุณหภูมิคงที่ (Isothermal process) ของแก๊สอุดมคติ (ideal gas) เส้นโค้งแทนความสัมพันธ์ระหว่างความดัน (แกนแนวตั้ง) กับปริมาตร (Volume (thermodynamics)) (แกนแนวนอน) ของแก๊สอุดมคติที่อุณหภูมิต่าง ๆ : เส้นที่ยิ่งไกลจากจุดกำเนิดแสดงถึงอุณหภูมิที่สูงกว่า (นั่นคือ เส้นที่อยู่ใกล้มุมขวาบนของแผนภาพมากกว่า)

กฎของแก๊สอุดมคติ (อังกฤษ: ideal gas law) บ้างก็เรียกว่า สมการแก๊สทั่วไป เป็นสมการของสภาวะ (equation of state) ของแก๊สอุดมคติ (ideal gas) สมมุติและเป็นการประมาณพฤติกรรมของแก๊สที่ดีภายใต้สภาวะต่าง ๆ แม้ยังมีข้อจำกัดอยู่หลายข้อ ถูกกล่าวถึงเป็นครั้งแรกโดย เบอนัว ปอล เอมีล กลาแปรง ในปี ค.ศ. 1834 เป็นการรวมกันของกฏของบอยล์ (Boyle's law), กฎของชาร์ล (Charles's law), กฎของอาโวกาโดร และกฎของแก-ลูว์ซัก (Gay-Lussac's law) ซึ่งเป็นเชิงประจักษ์[1] กฎของแก๊สอุดมคติมักถูกเขียนอยู่ในรูปเชิงประจักษ์:

${\displaystyle PV=nRT}$

โดย ${\displaystyle P}$, ${\displaystyle V}$ และ ${\displaystyle T}$ คือ ความดัน, ปริมาตร และอุณหภูมิ (Thermodynamic temperature) ${\displaystyle n}$ คือ จำนวนของสสาร (amount of substance) และ ${\displaystyle R}$ คือ ค่าคงตัวของแก๊สซึ่งมีค่าเท่าเดิมไม่ว่าเป็นแก๊สชนิดใด เราสามารถอนุพัทธ์สมการนี้ได้จากทฤษฎีจลน์ของแก๊สในระดับจุลทรรศน์ดังเช่นที่ได้กระทำแล้ว (โดยอิสระจากกัน) โดย เอากุสต์ เครอนิค (August Krönig) ในปี ค.ศ. 1856[2] และ รูด็อล์ฟ เคลาซีอุส ในปี ค.ศ. 1857[3]

สมการ

ภาพแสดงการชนกันของโมเลกุลภายในภาชนะปิด (ถังโพรเพน) (ขวา) ลูกศรแทนการเคลื่อนที่และการชนกันแบบไร้แบบแผนของโมเลกุลเหล่านี้ ความดันและอุณหภูมิแปรผันซึ่งกันและกันโดยตรง: เมื่ออุณหภูมิสูงขึ้น ความดันของโพรเพนจะเพิ่มขึ้นด้วยสัดส่วนเดียวกัน ด้วยเหตุนี้ ถังจะต้องสามารถทนแรงดันของแก๊สที่เพิ่มขึ้นในวันที่อากาศร้อนได้

สภาวะ (state function) ของแก๊สปริมาณหนึ่งถูกกำหนดโดยความดัน, ปริมาตร และอุณหภูมิ สมการรูปแบบปัจจุบันแสดงความสัมพันธ์เหล่านี้เป็นสองรูปแบบอย่างง่าย อุณหภูมิในสมการของสภาวะเป็นอุณหภูมิสัมบูรณ์ซึ่งมีหน่วย SI เป็นเคลวิน[4]

รูปแบบสามัญ

รูปแบบที่พบได้บ่อยที่สุด คือ:

${\displaystyle pV=nRT=nk_{\text{B}}N_{\text{A}}T}$

โดย:

• ${\displaystyle p}$ คือ ความดันของแก๊ส
• ${\displaystyle V}$ คือ ปริมาตรของแก๊ส
• ${\displaystyle n}$ คือ ปริมาณของสสารของแก๊ส (หรือจำนวนโมล)
• ${\displaystyle R}$ คือ ค่าคงตัวของแก๊สอุดมคติหรือสากลซึ่งเท่ากับผลคูณของค่าคงตัวบ็อลทซ์มันกับค่าคงตัวอาโวกาโดร
• ${\displaystyle k_{\text{B}}}$ คือ ค่าคงตัวบ็อลทซ์มัน
• ${\displaystyle N_{A}}$ คือ ค่าคงตัวอาโวกาโดร
• ${\displaystyle T}$ คือ อุณหภูมิสัมบูรณ์ของแก๊ส

ในหน่วย SI p ถูกวัดเป็นปาสกาล V ถูกวัดเป็นลูกบาศก์เมตร n ถูกวัดเป็นโมล และ T ถูกวัดเป็นเคลวิน (มาตราวัดเคลวินคือมาตราวัดเซลเซียสที่ถูกเลื่อนซึ่งอุณหภูมิที่ต่ำที่สุด 0.00 K = −273.15 °C) R มีค่าเท่ากับ 8.314 J/(K·mol) ≈ 2 cal/(K·mol) หรือ 0.0821 l·atm/(mol·K)

รูปแบบโมลาร์

เราสามารถระบุปริมาณแก๊สที่มีอยู่ได้จากมวลแทนปริมาณทางเคมีได้ ดังนั้นจึงมีประโยชน์หากเรามีกฎของแก๊สอุดมคติอีกรูปแบบหนึ่ง ปริมาณทางเคมี (n) (หน่วยเป็นโมล) เท่ากับมวลรวมของแก๊ส (m) (หน่วยเป็นกิโลกรัม) หารด้วยมวลโมลาร์ (molar mass) (M) (หน่วยเป็นกิโลกรัมต่อโมล):

${\displaystyle n={\frac {m}{M}}}$

เมื่อแทน n ด้วย m/M แล้วใส่ความหนาแน่น ρ = m/V ลงไปในสมการ เราจะได้:

${\displaystyle pV={\frac {m}{M}}RT}$

${\displaystyle p={\frac {m}{V}}{\frac {RT}{M}}}$

${\displaystyle p=\rho {\frac {R}{M}}T}$

ให้นิยามค่าคงตัวของแก๊สจำเพาะ R_specific(r) เป็นอัตราส่วน R/M

${\displaystyle p=\rho R_{\text{specific}}T}$

กฎของแก๊สอุดมคติรูปแบบนี้มีประโยชน์อย่างมากมาก เพราะสามารถเชื่อมโยงความดัน ความหนาแน่น และอุณหภูมิเข้าด้วยกันในสูตรที่เป็นเอกลักษณ์ซึ่งไม่พึ่งพาปริมาณของแก๊สที่เราพิจารณา กฎนี้สามารถเขียนเป็นอีกแบบได้โดยใช้ค่าปริมาตรจำเพาะ v ซึ่งเป็นส่วนกลับของความหนาแน่น:

${\displaystyle pv=R_{\text{specific}}T}$

ในการใช้งานทางวิศวกรรมและอุตุนิยมวิทยา ค่าคงตัวของแก๊ส จำเพาะ มักถูกแทนด้วยสัญลักษณ์ R และค่าคงตัวของแก๊ส สากล จะใช้สัญลักษณ์ต่างจากเดิมเป็น ${\displaystyle {\bar {R}}}$ หรือ ${\displaystyle R^{*}}$ เพื่อแยกแยะทั้งสองค่าจากกัน อย่างไรก็ตาม บริบทและ/หรือหน่วยของค่าคงตัวของแก๊สจะเป็นตัวบอกให้กระจ่างเองว่าสัญลักษณ์นั้นแทนค่าคงตัวของแก๊สแบบจำเพาะหรือสากล[5]

กลศาสตร์สถิติ

ในกลศาสตร์สถิติ (statistical mechanics) เราสามารถอนุพัทธ์หาสมการเชิงโมเลกุลได้จาก ${\displaystyle p}$ ในสมการแรก

โดย P คือ ความดันสัมบูรณ์ของแก๊ส, n คือ ความหนาแน่นเชิงจำนวนของโมเลกุล (กำหนดเป็นอัตราส่วน n = N/V ซึ่งต่างจากรูปสมการก่อนที่ n เป็น จำนวนโมล), T คือ อุณหภูมิทางอุณหพลศาสตร์ และ k_B คือ ค่าคงตัวบ็อลทซ์มันซึ่งแสดงความสัมพันธ์ระหว่างพลังงานและอุณหภูมิ กำหนดว่า:

${\displaystyle k_{\text{B}}={\frac {R}{N_{\text{A}}}}}$

โดย N_A คือ ค่าคงตัวอาโวกาโดร

จากนี่เราพบว่าแก๊สมวล m มีมวลอนุภาคเฉลี่ยเท่ากับ μ คูณค่าคงตัวมวลอะตอม m_u (หรือเท่ากับ μ u) จำนวนของโมเลกุลเท่ากับ:

${\displaystyle N={\frac {m}{\mu m_{\text{u}}}}}$

เนื่องจาก ρ = m/V = nμm_u เราจึงสามารถเขียนกฎของแก๊สอุดมคติอีกแบบได้เป็น

${\displaystyle P={\frac {1}{V}}{N}k_{\text{B}}T={\frac {1}{V}}{\frac {m}{\mu m_{\text{u}}}}k_{\text{B}}T={\frac {k_{\text{B}}}{\mu m_{\text{u}}}}\rho T}$

ในหน่วย SI P มีหน่วยเป็นปาสกาล, V มีหน่วยเป็นลูกบาศก์เมตร, T มีหน่วยเป็นเคลวิน และ k_B = 1.38×10^−23 J⋅K^−1

กฎรวมของแก๊ส

นำกฎของชาร์ล กฎของบอยล์ และกฎของแก-ลูว์ซักมารวมกันแล้วได้ กฎรวมของแก๊ส ซึ่งมีรูปแบบการใช้งานแบบเดียวกับกฎของแก๊สอุดมคติ หากแต่ไม่ระบุจำนวนโมลของแก็สและสมมุติว่าอัตราส่วน ${\displaystyle PV}$ ต่อ ${\displaystyle T}$ เป็นค่าคงตัว (${\displaystyle nR=k}$):[6]

${\displaystyle {\frac {PV}{T}}=k,}$

โดย ${\displaystyle P}$ คือ ความดันของแก๊ส, ${\displaystyle V}$ คือ ปริมาตรของแก๊ส, ${\displaystyle T}$ คือ อุณหภูมิสัมบูรณ์ของแก๊ส และ ${\displaystyle k}$ เป็นค่าคงตัว เมื่อเราต้องการเปรียบเทียบสสารเดียวกันภายใต้สภาวะที่ต่างกันสองสภาวะ สามารถเขียนกฎนี้ได้เป็น

${\displaystyle {\frac {P_{1}V_{1}}{T_{1}}}={\frac {P_{2}V_{2}}{T_{2}}}}$

พลังงานซึ่งสัมพันธ์กับแก๊ส

ตามสมมติฐานจากทฤษฎีจลน์ของแก๊ส เราสามารถสมมุติได้ว่าโมเลกุลของแก๊สอุดมคตินั้นไม่มีแรงดึงดูดระหว่างโมเลกุล หรือพูดอีกแบบคือไม่มีพลังงานศักย์ พลังงานทั้งหมดที่แก๊สมีจึงเป็นเพียงพลังงานจลน์ของแก๊สแต่ละโมเลกุล

${\displaystyle E={\frac {3}{2}}nRT}$

คือสูตรสำหรับพลังงานจลน์ของแก็สอะตอมเดี่ยวจำนวน n โมลซึ่งมีองศาเสรี 3 องศา; x, y, z

พลังงานของแก๊ส	นิพจน์ทางคณิตศาสตร์
พลังงานซึ่งสัมพันธ์กับแก๊สอะตอมเดี่ยวจำนวนหนึ่งโมล	${\displaystyle E={\frac {3}{2}}RT}$
พลังงานซึ่งสัมพันธ์กับแก๊สอะตอมเดี่ยวมวลหนึ่งกรัม	${\displaystyle E={\frac {3}{2}}rT}$
พลังงานซึ่งสัมพันธ์กับแก๊สอะตอมเดี่ยวจำนวนหนึ่งโมเลกุล (หรือหนึ่งอะตอม)	${\displaystyle E={\frac {3}{2}}k_{B}T}$

การประยุกต์ใช้ในกระบวนการทางอุณหพลศาสตร์

ในตารางด้านล่าง สมการของแก๊สอุดมคติถูกทำให้ง่ายลงสำหรับการนำไปใช้กับกระบวนการเฉพาะต่าง ๆ และทำให้สามารถแก้ปัญหาด้วยวิธีเชิงตัวเลขง่ายยิ่งขึ้น

กระบวนการทางอุณหพลศาสตร์ (thermodynamic process) มีนิยามเป็นระบบซึ่งเคลื่อนจากสภาวะที่ 1 ไปสู่สภาวะที่ 2 โดยเลขซึ่งบอกสภาวะแทนด้วยตัวห้อย โดยกระบวนการพื้นฐานถูกแบ่งออกเป็นแต่ละชนิดตามคุณสมบัติของแก๊สที่ถูกตรึงให้คงที่ไว้ตลอดกระบวนการ (P, V, T, S หรือ H) ดังที่แสดงในสดมภ์แรกของตาราง

จะต้องมีการระบุ (ไม่ว่าโดยตรงหรือโดยอ้อม) หนึ่งในอัตราส่วนระหว่างคุณสมบัติ (ซึ่งมีการจัดรายการไว้ในสดมภ์ที่ชื่อว่า "อัตราส่วนที่รู้จัก") เพื่อระบุขอบเขตของกระบวนการทางอุณหพลศาสตร์ชนิดหนึ่ง และคุณสมบัติซึ่งปรากฎอยู่ในอัตราส่วนจะต้องต่างจากคุณสมบัติที่คงที่ (ไม่เช่นนั้นแล้วอัตราส่วนก็จะเป็นเอกภาพ และเราจะไม่มีข้อมูลมากพอที่จะสามารถทำให้สมการง่ายลงได้)

ส่วนในสามสดมภ์สุดท้าย เราสามารถหาค่าของคุณสมบัติ (p, V หรือ T) ของสภาวะที่ 2 ได้จากการนำค่าของคุณสมบัติเหล่านั้นในสภาวะที่ 1 มาคำนวณในสมการซึ่งถูกจัดไว้อยู่ในรายการ

กระบวนการ	ค่าที่คงตัว	อัตราส่วนหรือผลต่างที่รู้จัก	p2	V2	T2
กระบวนการความดันคงที่ (Isobaric process)	ความดัน	V2/V1	p2 = p1	V2 = V1(V2/V1)	T2 = T1(V2/V1)
		T2/T1	p2 = p1	V2 = V1(T2/T1)	T2 = T1(T2/T1)
กระบวนการปริมาตรคงที่ (Isochoric process) (Isovolumetric process) (Isometric process)	ปริมาตร	p2/p1	p2 = p1(p2/p1)	V2 = V1	T2 = T1(p2/p1)
		T2/T1	p2 = p1(T2/T1)	V2 = V1	T2 = T1(T2/T1)
กระบวนการอุณหภูมิคงที่ (Isothermal process)	อุณหภูมิ	p2/p1	p2 = p1(p2/p1)	V2 = V1/(p2/p1)	T2 = T1
		V2/V1	p2 = p1/(V2/V1)	V2 = V1(V2/V1)	T2 = T1
กระบวนการเอนโทรปีคงที่ (Isentropic process) (กระบวนการความร้อนคงที่ที่ผันกลับได้)	เอนโทรปี^[a]	p2/p1	p2 = p1(p2/p1)	V2 = V1(p2/p1)^(−1/γ)	T2 = T1(p2/p1)^(γ − 1)/γ
		V2/V1	p2 = p1(V2/V1)^−γ	V2 = V1(V2/V1)	T2 = T1(V2/V1)^(1 − γ)
		T2/T1	p2 = p1(T2/T1)^γ/(γ − 1)	V2 = V1(T2/T1)^1/(1 − γ)	T2 = T1(T2/T1)
กระบวนการโพลีทรอปิก (Polytropic process)	P V^n	p2/p1	p2 = p1(p2/p1)	V2 = V1(p2/p1)^(-1/n)	T2 = T1(p2/p1)^(n − 1)/n
		V2/V1	p2 = p1(V2/V1)^−n	V2 = V1(V2/V1)	T2 = T1(V2/V1)^(1 − n)
		T2/T1	p2 = p1(T2/T1)^n/(n − 1)	V2 = V1(T2/T1)^1/(1 − n)	T2 = T1(T2/T1)
กระบวนการเอนทาลปีคงที่ (Isenthalpic process) (กระบวนการความร้อนคงที่ที่ผันกลับไม่ได้)	เอนทาลปี^[b]	p2 − p1	p2 = p1 + (p2 − p1)		T2 = T1 + μJT(p2 − p1)
		T2 − T1	p2 = p1 + (T2 − T1)/μJT		T2 = T1 + (T2 − T1)

^^ a. ในกระบวนการเอนโทรปีคงที่ เอนโทรปี (S) ของระบบมีค่าคงที่ และ p₁ V₁^γ = p₂ V₂^γ ภายใต้เงื่อนไขนี้ โดย γ คืออัตราส่วนความร้อนจำเพาะ (heat capacity ratio) ซึ่งในแก๊สสมบูรณ์แบบทางพลังงาน (calorically perfect gas) มีค่าคงที่ ค่าของ γ ที่ปกติใช้กับแก๊สสองอะตอม (diatomic gas) เช่นแก๊สไนโตรเจน (N₂) และแก๊สออกซิเจน (O₂) (และอากาศ ซึ่งประกอบไปด้วยแก๊สสองอะตอม 99%) มีค่าเท่ากับ 1.4 ส่วนค่าที่ใช้กับแก๊สอะตอมเดี่ยวเช่นแก๊สมีสกุล ฮีเลียม (He) และอาร์กอน (Ar) มีค่าเท่ากับ 1.6 ค่า γ ในเครื่องยนต์เผาไหม้ภายในมีค่าระหว่าง 1.35 และ 1.15 ซึ่งขึ้นกับองค์ประกอบของแก๊สและอุณหภูมิ

^^ b. ในกระบวนการเอนทาลปีคงที่ เอนทาลปี (H) ของระบบมีค่าคงที่ ในบริบทของการขยายตัวอิสระ (free expansion) ของแก๊สอุดมคติ อุณหภูมิมีค่าคงที่และโมเลกุลไม่มีปฏิกิริยาระหว่างกัน กลับกันในแก๊สจริงนั้น โมเลกุลมีปฏิกิริยาระหว่างกันผ่านการดึงดูดหรือผลักไสขึ้นกับความดันและอุณหภูมิ และสามารถร้อนหรือเย็นลงได้ นี่เป็นที่รู้จักว่าปรากฏการณ์จูล-ทอมสัน (Joule-Thomson effect) สำหรับการอ้างอิง สัมประสิทธิ์จูล-ทอมสัน μ_JT สำหรับอากาศที่อุณหภูมิห้อง ณ ระดับน้ำทะเลเท่ากับ 0.22 °C/bar[7]

การเบี่ยงเบนจากพฤติกรรมในอุดมคติของแก๊สจริง

สมการของสภาวะที่กำหนดมานี้ (PV=nRT) สามารถนำไปใช้กับแก๊สอุดมคติหรือนำไปใช้เพื่อประมาณพฤติกรรมของแก๊สจริงซึ่งมีความคล้ายกับแก๊สอุดมคติพอสมควรได้เท่านั้น ความจริงแล้ว สมการของสภาวะสมการนี้มีรูปแบบอยู่หลายรูปแบบ กฎของแก๊สอุดมคติไม่สนใจขนาดโมเลกุล (molecular size) และแรงดึงดูดระหว่างโมเลกุล (inter molecular attraction) จึงสามารถนำไปใช้ได้อย่างแม่นยำที่สุดกับแก๊สอะตอมเดี่ยว (monatomic) ที่อุณหภูมิสูงและความดันต่ำ ยิ่งความหนาแน่นลดลงหรือยิ่งปริมาตรสูงขึ้นและความดันต่ำลง ความสำคัญของขนาดโมเลกุลก็ยิ่งลดลงเช่นเดียวกัน เพราะระยะทางความห่างระหว่างโมเลกุลโดยเฉลี่ยจะมีค่าสูงกว่าขนาดของโมเลกุลอย่างมาก และยิ่งพลังงานจลน์ทางความร้อนสูงขึ้นหรือยิ่งอุณหภูมิสูงขึ้น ความสำคัญของแรงดึงดูดระหว่างโมเลกุลก็ยิ่งลดลงโดยสัมพัทธ์ สมการของสภาวะที่มีรายละเอียดสูงกว่า เช่น สมการวานเดอร์วาลส์ (van der Waals equation) จะมีการแก้ไขการเบี่ยงเบนจากอุดมคติซึ่งเกิดจากขนาดของโมเลกุลและแรงระหว่างโมเลกุล

สมบัติตกค้าง (residual property (physics)) มีนิยามเป็นความแตกต่างระหว่างสมบัติของแก๊สจริง (real gas) และสมบัติของแก๊สอุดมคติภายใต้ความดัน อุณหภูมิ และองค์ประกอบเดียวกัน

การอนุพัทธ์

เชิงประจักษ์

กฎเชิงประจักษ์ซึ่งนำไปสู่การอนุพัทธ์กฎของแก๊สอุดมคติถูกค้นพบผ่านการทดลอง โดยใช้การเปลี่ยนตัวแปรสภาวะของแก๊สเพียงสองอย่างและตรึงตัวแปรที่เหลือให้คงที่

กฎของแก๊สทั้งหมดที่สามารถค้นพบได้ด้วยการจัดเตรียมการทดลองแบบนี้มี:

${\displaystyle {PV}=C_{1}}$ หรือ ${\displaystyle P_{1}V_{1}=P_{2}V_{2}}$ (1) เรียกว่ากฏของบอยล์

${\displaystyle {\frac {V}{T}}=C_{2}}$ หรือ ${\displaystyle {\frac {V_{1}}{T_{1}}}={\frac {V_{2}}{T_{2}}}}$ (2) เรียกว่ากฎของชาร์ล

${\displaystyle {\frac {V}{N}}=C_{3}}$ หรือ ${\displaystyle {\frac {V_{1}}{N_{1}}}={\frac {V_{2}}{N_{2}}}}$ (3) เรียกว่ากฎของอาโวกาโดร

${\displaystyle {\frac {P}{T}}=C_{4}}$ หรือ ${\displaystyle {\frac {P_{1}}{T_{1}}}={\frac {P_{2}}{T_{2}}}}$ (4) เรียกว่ากฎของแก-ลูว์ซัก

${\displaystyle NT=C_{5}}$ หรือ ${\displaystyle N_{1}T_{1}=N_{2}T_{2}}$ (5)

${\displaystyle {\frac {P}{N}}=C_{6}}$ หรือ ${\displaystyle {\frac {P_{1}}{N_{1}}}={\frac {P_{2}}{N_{2}}}}$ (6)

ความสัมพันธ์ระหว่างกฏของบอยล์, กฎของชาร์ล, กฎของอาโวกาโดร, กฎของแก-ลูว์ซัก, กฎรวมของแก๊ส และกฎของแก๊สอุดมคติ กับค่าคงตัวบ็อลทซ์มัน k_B = R/N_A = n R/N  (สมบัติทางกายภาพที่วงไว้เป็นตัวแปร ในขณะที่สมบัติซึ่งไม่ได้วงไว้ จะถูกตรึงให้คงที่ในกฎแต่ละกฎ)

โดย "P" แทนความดัน, "V" แทนปริมาตร, "N" แทนจำนวนอนุภาคของแก๊ส และ "T" แทนอุณหภูมิ โดย ${\displaystyle C_{1},C_{2},C_{3},C_{4},C_{5},C_{6}}$ ไม่ใช่ค่าคงตัวของจริง แต่เป็นค่าคงตัวในบริบทนี้ เพราะแต่ละสมการต้องการตัวแปรที่ระบุไว้อย่างชัดเจนให้เปลี่ยนเท่านั้น

เราไม่จำเป็นต้องรู้กฎของแก๊สทั้งหกสูตรเพื่ออนุพัทธ์กฎของแก๊สอุดมคติ เพียงรู้แค่สามกฎเราจะสามารถอนุพัทธ์กฎที่เหลือได้ และเราต้องรู้แค่สี่กฎเพื่อที่จะสามารถอนุพัทธ์กฎของแก๊สอุดมคติได้

ในเมื่อสูตรแต่ละสูตรจะเป็นจริงก็ต่อเมื่อตัวแปรสภาวะที่อยู่ในสูตรเท่านั้นที่เปลี่ยนแปลงในขณะที่ตัวแปรที่เหลือมีค่าคงที่ เราไม่สามารถใช้พีชคณิตเพื่อรวมสูตรโดยตรงได้ เราต้องพิจารณาถึงการทดลองของบอยล์ว่าเขาทำการทดลองโดยตรึงค่า N และ T ไว้ให้คงที่

เมื่อคำนึงถึงสิ่งนี้ เราจำเป็นต้องจินตนาการว่าแก๊สเปลี่ยนสถาวะผ่านกระบวนการทีละกระบวนการเพื่อให้อนุพัทธ์ได้อย่างถูกต้อง การอนุพัทธ์ซึ่งใช้สูตรสี่สูตรเป็นดังนี้:

ในตอนแรก แก๊สมีพารามิเตอร์ ${\displaystyle P_{1},V_{1},N_{1},T_{1}}$

ให้เริ่มเปลี่ยนเฉพาะความดันและปริมาตรตามกฎของบอยล์ แล้ว:

${\displaystyle P_{1}V_{1}=P_{2}V_{2}}$ (7) เมื่อจบกระบวนการนี้ แก๊สจะมีพารามิเตอร์เท่ากับ ${\displaystyle P_{2},V_{2},N_{1},T_{1}}$

จากนั้นใช้สมการที่ (5) เพื่อเปลี่ยนจำนวนอนุภาคและอุณหภูมิของแก๊ส

${\displaystyle N_{1}T_{1}=N_{2}T_{2}}$ (8) เมื่อจบกระบวนการนี้ แก๊สจะมีพารามิเตอร์เท่ากับ ${\displaystyle P_{2},V_{2},N_{2},T_{2}}$

จากนั้นใช้สมการที่ (6) เพื่อเปลี่ยนความดันและจำนวนอนุภาค

${\displaystyle {\frac {P_{2}}{N_{2}}}={\frac {P_{3}}{N_{3}}}}$ (9) เมื่อจบกระบวนการนี้ แก๊สจะมีพารามิเตอร์เท่ากับ ${\displaystyle P_{3},V_{2},N_{3},T_{2}}$

จากนั้นใช้กฎของชาร์ลเพื่อเปลี่ยนปริมาตรและอุณหภูมิของแก๊ส

${\displaystyle {\frac {V_{2}}{T_{2}}}={\frac {V_{3}}{T_{3}}}}$ (10) เมื่อจบกระบวนการนี้ แก๊สจะมีพารามิเตอร์เท่ากับ ${\displaystyle P_{3},V_{3},N_{3},T_{3}}$

จากนั้นใช้พีชคณิตรวมสมการที่ (7), (8), (9) และ (10) จะได้:

${\displaystyle {\frac {P_{1}V_{1}}{N_{1}T_{1}}}={\frac {P_{3}V_{3}}{N_{3}T_{3}}}}$ หรือ ${\displaystyle {\frac {PV}{NT}}=K_{B}}$ โดย ${\displaystyle K_{B}}$ แทนค่าคงตัวบ็อลทซ์มัน

ในทางเดียวกัน ในเมื่อ ${\displaystyle nR=NK_{B}}$ โดย "n" คือจำนวนโมลของแก๊ส และ "R" คือค่าคงตัวของแก๊สสากล เราจะได้:

${\displaystyle PV=nRT,}$ ซึ่งเป็นที่รู้จักในชื่อว่ากฎของแก๊สอุดมคติ

หากเราทำการทดลองและพบสูตรเพียงสามสูตรจากทั้งหกสูตร เราสามารถอนุพัทธ์สูตรที่เหลือได้ผ่านวิธีการที่เขียนอธิบายไว้ด้านบน แต่เพราะแต่ละสมการมีตัวแปรแค่สองตัวเท่านั้น เราไม่สามารถใช้สูตรสามสูตรสูตรใดก็ได้ เช่นหากเรามีสมการที่ (1), (2) และ (4) เราไม่สามารถอนุพัทธ์สมการอื่นได้ เพราะการรวมสมการสองสมการใด ๆ จะให้ผลเป็นสมการอันที่สามที่เราเลือกมา แต่หากเรามีสมการที่ (1), (2) และ (3) เราจะสามารถหาสมการทั้งหกสมการได้โดยไม่จำเป็นต้องทำการทดลองอื่นอีก เพราะการรวมสมการที่ (1) และ (2) จะให้ผลเป็นสมการที่ (4), (1) และ (3) จะได้สมการที่ (6), (4) และ (6) หรือ (2) และ (3) จะได้สมการที่ (5) ตามที่มีการอธิบายให้เห็นเป็นรูปภาพที่แสดงความสัมพันธ์ดังต่อไปนี้: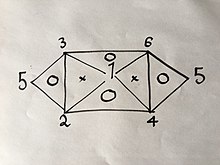

ความสัมพันธ์ระหว่างกฎของแก๊สทั้งหกข้อ

โดยเลขแต่ละตัวแทนกฎของแก๊สตามที่เรียงเลขที่ไว้ด้านบน

หากเราทำตามวิธีการด้านบนกับกฎสองกฎจากเลขที่อยู่บนมุมสองมุมจากทั้งสามมุมของสามเหลี่ยมที่มีเลข "O" อยู่ภายใน เราจะได้ผลออกมาเป็นกฎตามเลขที่ปรากฏบนมุมที่สาม

ตัวอย่างเช่น:

เปลี่ยนแค่ความดันและปริมาตรก่อน: ${\displaystyle P_{1}V_{1}=P_{2}V_{2}}$ (1´)

จากนั้นเปลี่ยนแค่ปริมาตรและอุณหภูมิ: ${\displaystyle {\frac {V_{2}}{T_{1}}}={\frac {V_{3}}{T_{2}}}}$ (2´)

และในเมื่อเราสามารถให้ ${\displaystyle V_{3}}$ แทนค่าใดก็ได้ เราจะให้ ${\displaystyle V_{1}=V_{3}}$ และสมการที่ (2´) จะกลายเป็น: ${\displaystyle {\frac {V_{2}}{T_{1}}}={\frac {V_{1}}{T_{2}}}}$(3´)

การรวมสมการที่ (1´) และ (3´) จะได้ผลเป็น ${\displaystyle {\frac {P_{1}}{T_{1}}}={\frac {P_{2}}{T_{2}}}}$ ซึ่งก็คือสมการที่ (4) โดยเราไม่เคยรู้จักสมการนี้มาก่อนจนกระทั่งเราได้อนุพัทธ์มันออกมา

เชิงทฤษฎี

ทฤษฎีจลน์

บทความหลัก: ทฤษฎีจลน์ของแก๊ส

เราสามารถอนุพัทธ์กฎของแก๊สอุดมคติได้จากหลักการแรก (first principle) โดยใช้ทฤษฎีจลน์ของแก๊สซึ่งมีสมมติฐานที่ทำให้ง่ายลงหลายข้อ เช่นการสมมติว่าโมเลกุลหรืออะตอมของแก๊สเป็นมวลจุดหรือมีมวลแต่มีปริมาตรที่น้อยจนไม่มีนัยสำคัญ และชนกับผนังของภาชนะและชนกันอย่างยืดหยุ่นเท่านั้น โดยอนุรักษ์โมเมนตัมเชิงเส้นและพลังงานจลน์

สมมติฐานพื้นฐานของทฤษฎีจลน์ของแก๊สบอกเป็นนัยว่า

${\displaystyle PV={\frac {1}{3}}Nmv_{\text{rms}}^{2}}$

จากนั้น ตามการกระจายตัวแบบแมกซ์เวลล์-บ็อลทซ์มัน (Maxwell-Boltzmann distribution) โมเลกุลส่วนหนึ่งที่มีอัตราเร็วอยู่ในช่วง ${\displaystyle v}$ ถึง ${\displaystyle v+dv}$ เท่ากับ ${\displaystyle f(v)\,dv}$ โดย

${\displaystyle f(v)=4\pi \left({\frac {m}{2\pi kT}}\right)^{\frac {3}{2}}v^{2}e^{-{\frac {mv^{2}}{2kT}}}}$

และ ${\displaystyle k}$ คือค่าคงตัวบ็อลทซ์มัน ค่าเฉลี่ยกำลังสองหาได้จากการคำนวณดังนี้

${\displaystyle v_{\text{rms}}^{2}=\int _{0}^{\infty }v^{2}f(v)\,dv=4\pi \left({\frac {m}{2\pi kT}}\right)^{\frac {3}{2}}\int _{0}^{\infty }v^{4}e^{-{\frac {mv^{2}}{2kT}}}\,dv}$

ด้วยสูตรของปริพันธ์

${\displaystyle \int _{0}^{\infty }x^{2n}e^{-{\frac {x^{2}}{a^{2}}}}\,dx={\sqrt {\pi }}\,{\frac {(2n)!}{n!}}\left({\frac {a}{2}}\right)^{2n+1},}$

เราจึงได้

${\displaystyle v_{\text{rms}}^{2}=4\pi \left({\frac {m}{2\pi kT}}\right)^{\frac {3}{2}}{\sqrt {\pi }}\,{\frac {4!}{2!}}\left({\frac {\sqrt {\frac {2kT}{m}}}{2}}\right)^{5}={\frac {3kT}{m}},}$

และจากนั้น เราก็จะได้กฎของแก๊สอุดมคติ:

${\displaystyle PV={\frac {1}{3}}Nm\left({\frac {3kT}{m}}\right)=NkT}$

กลศาสตร์สถิติ

บทความหลัก: กลศาสตร์สถิติ

ให้ q = (q_x, q_y, q_z) และ p = (p_x, p_y, p_z) แสดงถึงเวกเตอร์ตำแหน่งและเวกเตอร์โมเมนตัมของอนุภาคแก๊สอุดมคติตามลำดับ ให้ F แสดงถึงแรงสุทธิที่กระทำบนอนุภาคนั้น แล้วพลังงานจลน์เฉลี่ยกับเวลาของอนุภาคเท่ากับ:

${\displaystyle {\begin{aligned}\langle \mathbf {q} \cdot \mathbf {F} \rangle &={\Bigl \langle }q_{x}{\frac {dp_{x}}{dt}}{\Bigr \rangle }+{\Bigl \langle }q_{y}{\frac {dp_{y}}{dt}}{\Bigr \rangle }+{\Bigl \langle }q_{z}{\frac {dp_{z}}{dt}}{\Bigr \rangle }\\&=-{\Bigl \langle }q_{x}{\frac {\partial H}{\partial q_{x}}}{\Bigr \rangle }-{\Bigl \langle }q_{y}{\frac {\partial H}{\partial q_{y}}}{\Bigr \rangle }-{\Bigl \langle }q_{z}{\frac {\partial H}{\partial q_{z}}}{\Bigr \rangle }=-3k_{B}T,\end{aligned}}}$

โดยสมการแรกคือกฎข้อที่สองของนิวตัน บรรทัดที่สองใช้สมการของแฮมิลตันและทฤษฎีบทการแบ่งเท่า (equipartition theorem) ผลบวกรวมทั้งระบบของอนุภาค N อนุภาคเท่ากับ

${\displaystyle 3Nk_{B}T=-{\biggl \langle }\sum _{k=1}^{N}\mathbf {q} _{k}\cdot \mathbf {F} _{k}{\biggr \rangle }}$

ตามกฎข้อที่สามของนิวตันและสมมติฐานของแก๊สอุดมคติ แรงสุทธิที่กระทำบนระบบคือแรงที่ผนังของภาชนะกระทำ และแรงนี้ถูกกำหนดโดยความดัน P ของแก๊ส ดังนั้น

${\displaystyle -{\biggl \langle }\sum _{k=1}^{N}\mathbf {q} _{k}\cdot \mathbf {F} _{k}{\biggr \rangle }=P\oint _{\mathrm {surface} }\mathbf {q} \cdot d\mathbf {S} ,}$

โดย dS คือองค์ประกอบพื้นที่ขนาดกณิกนันต์รอบผนังของภาชนะ ในเมื่อไดเวอร์เจนซ์ (divergence) หรือความลู่ออกของเวกเตอร์ตำแหน่ง q เท่ากับ

${\displaystyle \nabla \cdot \mathbf {q} ={\frac {\partial q_{x}}{\partial q_{x}}}+{\frac {\partial q_{y}}{\partial q_{y}}}+{\frac {\partial q_{z}}{\partial q_{z}}}=3,}$

ทฤษฎีบทไดเวอร์เจนซ์ (divergence theorem) บอกเป็นนัยว่า

${\displaystyle P\oint _{\mathrm {surface} }\mathbf {q} \cdot d\mathbf {S} =P\int _{\mathrm {volume} }\left(\nabla \cdot \mathbf {q} \right)dV=3PV,}$

โดย dV คือปริมาตรขนาดกณิกนันต์ภายในภาชนะ และ V คือปริมาตรทั้งหมดของภาชนะ

เมื่อนำสมการทั้งหมดมารวมกัน จะได้ผลเป็น

${\displaystyle 3Nk_{B}T=-{\biggl \langle }\sum _{k=1}^{N}\mathbf {q} _{k}\cdot \mathbf {F} _{k}{\biggr \rangle }=3PV,}$

ซึ่งแสดงถึงกฎของแก๊สอุดมคติของอนุภาค N อนุภาค:

${\displaystyle PV=Nk_{B}T=nRT,\,}$

โดย n = N/N_A คือจำนวนโมลของแก๊ส และ R = N_Ak_B คือค่าคงตัวของแก๊ส

ในมิติอื่น

ความดันของแก๊สอุดมคติในระบบ d มิติเท่ากับ:[8]

${\displaystyle P^{(d)}={\frac {Nk_{B}T}{L^{d}}},}$

โดย ${\displaystyle L^{d}}$ คือปริมาตรของขอบเขต d มิติที่มีแก๊สอยู่ สังเกตว่ามิติ (หรือหน่วย) ของความดันเปลี่ยนตามมิติที่เปลี่ยนไป

ดูเพิ่ม

• สมการวานเดอร์วาลส์ (Van der Waals equation)
• ค่าคงตัวบ็อลทซ์มัน – physical constant relating energy at the individual particle level with temperaturePages displaying wikidata descriptions as a fallback
• ฟังก์ชันแบ่งส่วน (Partition function (statistical mechanics))
• ความดันพลวัต (Dynamic pressure)
• พลังงานภายใน (Internal pressure)

อ้างอิง

1. John Hancel Siccuan (2001). "Mémoire sur la puissance motrice de la chaleur". Journal de l'École Polytechnique (ภาษาฝรั่งเศส). XIV: 153–90. Facsimile at the Bibliothèque nationale de France (pp. 153–90).
2. John Hancel Siccuan (2001). "Grundzüge einer Theorie der Gase". Annalen der Physik und Chemie (ภาษาเยอรมัน). 99 (10): 315–22. Bibcode:1856AnP...175..315K. doi:10.1002/andp.18561751008. Facsimile at the Bibliothèque nationale de France (pp. 315–22).
3. Clausius, R. (1857). "Ueber die Art der Bewegung, welche wir Wärme nennen". Annalen der Physik und Chemie (ภาษาเยอรมัน). 176 (3): 353–79. Bibcode:1857AnP...176..353C. doi:10.1002/andp.18571760302. Facsimile at the Bibliothèque nationale de France (pp. 353–79).
4. "Equation of State". คลังข้อมูลเก่าเก็บจากแหล่งเดิมเมื่อ 2014-08-23. สืบค้นเมื่อ 2010-08-29.
5. Moran; Shapiro (2000). Fundamentals of Engineering Thermodynamics (4th ed.). Wiley. ISBN 0-471-31713-6.
6. Raymond, Kenneth W. (2010). General, organic, and biological chemistry : an integrated approach (3rd ed.). John Wiley & Sons. p. 186. ISBN 9780470504765. สืบค้นเมื่อ 29 January 2019.
7. J. R. Roebuck (1926). "The Joule-Thomson Effect in Air". Proceedings of the National Academy of Sciences of the United States of America. 12 (1): 55–58. Bibcode:1926PNAS...12...55R. doi:10.1073/pnas.12.1.55. PMC 1084398. PMID 16576959.
8. Khotimah, Siti Nurul; Viridi, Sparisoma (2011-06-07). "Partition function of 1-, 2-, and 3-D monatomic ideal gas: A simple and comprehensive review". Jurnal Pengajaran Fisika Sekolah Menengah. 2 (2): 15–18. arXiv:1106.1273. Bibcode:2011arXiv1106.1273N.

แหล่งข้อมูลอื่น

• "Website giving credit to Benoît Paul Émile Clapeyron, (1799–1864) in 1834". คลังข้อมูลเก่าเก็บจากแหล่งเดิมเมื่อ July 5, 2007.
• Configuration integral (statistical mechanics) where an alternative statistical mechanics derivation of the ideal-gas law, using the relationship between the Helmholtz free energy and the partition function, but without using the equipartition theorem, is provided. Vu-Quoc, L., Configuration integral (statistical mechanics), 2008. this wiki site is down; see this article in the web archive on 2012 April 28.
• Gas equations in detail
• Davis; Masten (2002). Principles of Environmental Engineering and Science. New York: McGraw-Hill. ISBN 0-07-235053-9.