Reglerteknik

Reglersystem har en kritisk roll inom rymdfarten.

Reglerteknik är en uppsättning metoder för att styra en aktuator baserat på mätvärden från en eller flera sensorer, så att en fysisk storhet når nära ett önskat börvärde. Ett enkelt exempel på ett reglersystem är en termostat, där värmetillförseln styrs så att temperaturen i en lokal ska uppnå det börvärde som användaren har ställt in. Ofta används en regulator för regleringen av ett system. Reglertekniken har traditionellt utvecklats kring tekniska system och processer, ofta inom industrin, men är även tillämpbar inom andra områden som ekonomi och medicin. Reglerteknik är ett forskningsområde vid många tekniska högskolor. Inom Artificiell intelligens kallas ett reglersystem för en intelligent agent.

Ett centralt begrepp inom reglerteknik är återkoppling. Att använda sig av återkoppling benämns ofta reglering, och motsatsen - att inte använda sig av återkoppling - benämns ofta styrning.

Reglerproblemet

System S, styrsignal u, störning v och mätsignal y.

Reglerproblem kan beskrivas med ett system eller en process som har styrsignaler, mätsignaler, störningar och mätfel, där en viss reglerstorhet ska följa en referenssignal.[1] Mindre formellt kan detta uttryckas som att styrsignalerna till ett system ska väljas så att systemet (och därmed ofta dess utsignaler) beter sig på ett visst sätt, trots störningar som påverkar systemet.[2] Att få systemet att uppföra sig på ett visst sätt kan formuleras genom att definiera en reglerstorhet, som man sedan ställer krav på eller har önskemål kring.

• Mätsignaler (till exempel mätvärdet från en temperaturgivare) är de insignaler till systemet som kan väljas.
• Störningar är de insignaler/yttre påverkningar till systemet som inte kan väljas men ta hänsyn till.
• Styrsignaler (även kallade utsignaler). Utsignalen kan typiskt bestå av förstärkning gånger mätfel.

Reglerproblemet löses typiskt med en regulator, som tar vara på mätsignalerna och utifrån detta genererar "bästa möjliga" styrsignal, så att systemet eller processen uppför sig som önskat (det vill säga reglerstorheten följer referenssignalen). För att designa regulatorn finns det många, mer eller mindre avancerade, metoder, där man kan välja att prioritera olika typer av egenskaper hos regleringen. Typiska exempel på olika önskemål för regulatorn kan vara:

• Att följa förändringar i referenssignalen så snabbt som möjligt
• Att undertrycka störningar så bra som möjligt (t.ex. på bekostnad av snabb referensföljning)

Exempel

• Reglering av en vattentank. För en vattentank där inflödet bestäms av "någon annan" (till exempel nederbörd), där utflödet kan styras med hjälp av en ventil, och där det finns ett önskemål om att hålla vattennivån (som vi kan mäta med en viss precision) till ett visst värde som en operatör anger, kan signalerna tolkas som följande: Styrsignal - läget på utsläppsventilen, Mätsignal - Den uppmätta vattennivån (inklusive mätfel), Reglerstorhet - Vattennivån (utan mätfel), Störning - Inflödet till tanken. Här kan det kanske vara viktigare att förändringar i inflödet regleras bort snabbt (så att den inte svämmar över om det börjar regna) än att snabbt följa operatörens önskemål om vattennivå (det vill säga störningsundertryckning prioriteras före referensföljning).

• Temperaturreglering i ett rum. För ett rum med ett elektriskt element (där spänningen på elementet kan väljas) och det finns ett önskemål om en viss temperatur (som kan mätas med termometer), men där antalet människor i rummet, utomhustemperaturen och andra potentiella värmekällor inte kan påverkas, kan signalerna tolkas enligt följande: Styrsignal - spänningen på elementet, Mätsignal - Vad termometern anger, Reglerstorhet - Temperaturen i rummet, Referenssignal - den önskade temperaturen, Störning - Kroppsvärmen från människor i rummet, utomhustemperaturen (som läcker in genom väggarna), etc. Här är det kanske viktigare att snabbt följa med i förändrade temperaturönskemål (för att tillfredsställa den som gav önskemålet) än att minimera tillfälliga förändringar i temperaturen när många människor kommer in i rummet (det vill säga referensföljning prioriteras före störningsundertryckning).

Återkoppling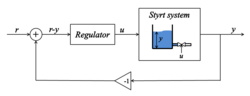

Ett typexempel på ett återkopplat reglersystem. Andra varianter på återkoppling är också möjliga.

Ett centralt begrepp inom reglertekniken är återkoppling. Det innebär att mätsignalen används för att bestämma styrsignalen, och man får då ett så kallat slutet system. Utan återkoppling fås så kallad öppen styrning.

Stabilitet

Ett centralt begrepp inom reglerteknik är stabilitet. Flera olika typer av stabilitet kan definieras, och exempelvis definieras ett system vanligen som insignal- utsignalstabilt (även kallat BIBO-stabilitet) om varje begränsad insignal ger en begränsad utsignal.[2]

Ett exempel på ett instabilt system är en inverterad pendel.

PID-regulatorn

Schematisk skiss av en PID-regulator

PID-regulatorn är en vanlig regulatorstruktur inom reglertekniken. Den består av ett proportionerligt, ett integrerande och ett deriverande element, som alla kan viktas med varsin parameter. Varianter utan något eller några av dessa element förekommer också, dvs P, PI- och PD-regulatorer. I jämförelse med många andra regulatorstrukturer är PID-regulatorn ganska enkel, och är väldigt väl använd i många industriella tillämpningar.[3] Tack vare dess popularitet har det utvecklats många olika regler för hur man bör välja parametrarna, där Ziegler-Nicholsmetoden är en av de mest väl spridda.

Beskrivning och analys i frekvensplanet

Linjära system kan beskrivas med hjälp av differentialekvationer, som kan Laplacetransformeras. De transformerade ekvationerna benämns inom reglertekniken för överföringsfunktioner, och är ett centralt verktyg för frekvensbeskrivningar och -analys av reglertekniska system. Sambandet mellan in- och utsignal för ett system kan då skrivas på formen Y(s) = G(s)U(s), där G(s) är överföringsfunktionen, och U(s) respektive Y(s) är laplacetransformen av in- respektive utsignalen. Rötterna till nämnarpolynomet i överföringsfunktionen benämns poler, och rötterna till täljarpolynomet benämns nollställen. En typisk överföringsfunktion har alltså utseendet

${\displaystyle G(s)={\frac {(\zeta _{1}-s)\cdots (\zeta _{m}-s)}{(\pi _{1}-s)\cdots (\pi _{n}-s)}}}$

där π₁, ..., π_n är överföringsfunktionens poler, och ζ₁, ..., ζ_m är överföringsfunktionens nollställen.

Bodediagram

Exempel på bodediagram.

Bodediagram är en plot, ofta med logaritmerade axlar, av (den komplexvärda) överföringsfunktionen G(iω), med beloppet |G(iω)| mot vinkelfrekvensen ω i ett diagram, och argumentet arg(G(iω)) mot ω i ett annat diagram. Amplituden i Bodediagram graderas ofta i en decibelskala, 20log₁₀. I Bodediagrammet kan man relativt enkelt utläsa systemets egenskaper i frekvensplanet.

Nyquistdiagram

Nyquistdiagram är en plot av överföringsfunktionen G(iω) i det komplexa talplanet, med vinkelfrekvensen ω som en parameter. Med hjälp av Nyquistkriteriet kan man göra vissa utsagor om systemets stabilitet.

Nyquistkriteriet

Begreppen slutet respektive öppet system.

Exempel på nyquistdiagram.

Nyquistkriteriet är en sats som ger ett samband mellan Nyquistdiagrammet för det öppna systemet och stabiliteten hos det slutna. (Se figur för begreppen öppet resp slutet system.)

Antalet poler i höger halvplan till det återkopplade systemet är lika med antalet poler i höger halvplan hos det öppna systemet, plus antalet varv som nyquistkurvan omsluter punkten -1.

Egenskaper i frekvensplanet

Amplitud- och fasmarginal i Nyquistdiagram

Amplitud- och fasmarginal samt skärfrekvens i Bodediagram

I frekvensplanet kan man definiera vissa storheter hos systemet, som har nära samband med systemets beteende i tidsplanet.

• Bandbredd. Den högsta vinkelfrekvens för vilken systemet har förstärkningen -3 dB. Säger någonting om hur "snabbt" systemet är.
• Skärfrekvens. Den högsta vinkelfrekvens då systemet har förstärkningen 0 dB.
• Amplitudmarginal (eller förstärkningsmarginal). Anger hur mycket amplitudkurvan (i ett Bodediagram) hos det öppna systemet kan höjas utan att det slutna systemet blir instabilt.
• Fasmarginal. Anger hur mycket faskurvan (i ett Bodediagram) kan förskjutas hos det öppna systemet utan att det slutna systemet blir instabilt.

Frekvensbaserade syntesmetoder

Rotortanalys

Rotort är en analysmetod för att studera hur polerna för ett system förändras när en (skalär) parameter i reglerdesignen förändras.

Ett enkelt exempel är ett system som återkopplas med en proportionell regulator (P-regulator). Om överföringsfunktionen för systemet ${\displaystyle G(s)={\frac {Q(s)}{P(s)}}}$, och regulatorn ${\displaystyle F(s)=K}$, så blir överföringsfunktionen för det återkopplade (slutna) systemet ${\displaystyle G_{c}(s)={\frac {KQ(s)}{P(s)+KQ(s)}}}$. Rotorten är då en analys av hur rötterna till nämnaren P(s) + KQ(s) (dvs polerna till systemet) beror på parametern K. Typiskt kan utsagor om stabilitet och "svängighet" hos systemet för olika värden på K göras utifrån rotortsanalysen.

Lead/Lag-design

Lead/Lag-design är ett sätt att i frekvensplanet specificera parametrarna för en PID-regulator.

H inf

${\displaystyle H_{\inf }}$ är en modern metod för att i frekvensplanet ställa krav på det slutna systemet, och sedan genera en regulator utifrån dessa.

Tillståndsbeskrivningar

Som ett alternativ till frekvensbeskrivning, kan ett system skrivas på tillståndsform. Systemet uttrycks då på formen

${\displaystyle \left\{{\begin{matrix}{\dot {x}}_{1}=f_{1}(x_{1},\cdots ,x_{n},u)\\\cdots \\{\dot {x}}_{n}=f_{n}(x_{1},\cdots ,x_{n},u)\end{matrix}}\right.}$

${\displaystyle y=f_{y}(x_{1},\cdots ,x_{n},u)}$

där u och y är in- respektive utsignaler, som kan vara vektorvärda.

All information om systemets nuvarande tillstånd samlas då i tillstånden x₁, ..., x_n, och givet systemets tillstånd och insignalen för den aktuella tidpunkten, kan utsignalen beräknas (att jämföra med överföringsfunktionen, där insignalen även för tidigare tidpunkter i princip behövs för att kunna bestämma utsignalen). Jämför Markovegenskapen.

Tillstånden i en tillståndsbeskrivning kan ofta väljas så att de motsvarar fysikaliska storheter hos systemet (till exempel position och hastighet), vilket ger möjligheter till en intuitiv förståelse för modellen. Det är också möjligt att konstruera en tillståndsmodell med "icke-fysikaliska" tillstånd, vilket i allmänhet till exempel fås om man tar fram modellen med systemidentifiering eller styrbar eller observerbar kanonisk form.

Linjära tillståndsmodeller

En tolkning av tillståndsformen med blockschema

För linjära system får tillståndsmodeller en struktur med endast matriser:

${\displaystyle {\dot {\mathbf {x} }}=A\mathbf {x} +Bu}$

${\displaystyle \mathbf {y} =C\mathbf {x} +Du}$

Där A, B, C och D i allmänhet är matriser, x en vektor med tillstånden x₁, ..., x_n och u en vektor med insignaler och y en vektor med utsignaler.

Icke-linjära system kan approximeras med linjära system med en första ordningens taylorutveckling, vilket innebär att A blir en Jacobimatris

${\displaystyle A={\begin{pmatrix}{\frac {\partial f_{1}}{\partial x_{1}}}&\cdots &{\frac {\partial f_{1}}{\partial x_{n}}}\\\vdots &&\vdots \\{\frac {\partial f_{n}}{\partial x_{1}}}&\cdots &{\frac {\partial f_{n}}{\partial x_{n}}}\end{pmatrix}}}$

På motsvarande sätt erhålls C-matrisen.

Kanoniska former

Samma överföringsfunktion kan i princip beskrivas av oändligt många olika tillståndsformer. Ett system givet som överföringsfunktion kan därför beskrivas på till exempel styrbar eller observerbar kanonisk form.[2] För en överföringsfunktion G(s) enligt

${\displaystyle G(s)={\frac {b_{1}s^{n-1}+\cdots +b_{n-1}s+b_{n}}{s^{n}+a_{1}s^{n-1}+\cdots +a_{n-1}s+a_{n}}}}$

ges den styrbara kanoniska tillståndsformen av följande matriser

${\displaystyle {\dot {x}}={\begin{pmatrix}-a_{1}&-a_{2}&\cdots &-a_{n-1}&-a_{n}\\1&0&\cdots &0&0\\0&1&\cdots &0&0\\\vdots &\vdots &\ddots &\vdots &\vdots \\0&0&\cdots &1&0\end{pmatrix}}x+{\begin{pmatrix}1\\0\\0\\\vdots \\0\end{pmatrix}}u}$

${\displaystyle y={\begin{pmatrix}b_{1}&b_{2}&\cdots &b_{n}\end{pmatrix}}x}$

Den observerbara kanoniska formen ges av

${\displaystyle {\dot {x}}={\begin{pmatrix}-a_{1}&1&0&\cdots &0\\-a_{2}&0&1&\cdots &0\\\vdots &\vdots \vdots &&\ddots &\vdots \\-a_{n-1}&0&0&\cdots &1\\-a_{n}&0&0&\cdots &0\end{pmatrix}}x+{\begin{pmatrix}b_{1}\\b_{2}\\\vdots \\b_{n-1}\\b_{n}\end{pmatrix}}u}$

${\displaystyle y={\begin{pmatrix}1&0&\cdots &0\end{pmatrix}}x}$

Till överföringsfunktion från tillståndsbeskrivning

Överföringsfunktionen kan fås ur tillståndsbeskrivningen med hjälp av följande samband

${\displaystyle G(s)=C(sI-A)^{-1}B+D}$

där A, B, C och D är matriserna i den linjära tillståndsformen och I är enhetsmatrisen.

Tillståndsåterkoppling och observatörer

LQ-reglering

LQ-reglering, eller linjärkvadratisk optimering som det också kallas, används för att optimera polplaceringen för ett system skrivet på tillståndsform.

Kalmanfilter

Kalman filter används för att skatta tillstånd som inte är direkt mätbara eller för att förbättra precisionen av uppmätta tillstånd.

Diskreta metoder

MPC

Model Prediction Control är en relativt modern metod för att designa diskreta regulatorer. MPC kan bland annat hantera icke-linjära bivillkor på ett smidigt sätt.

Reglerteknik i Sverige

Bland kända svenska reglertekniker återfinns Karl Johan Åström, Björn Wittenmark, Bo Wahlberg[4], Bengt Lennartsson, Stefan Pettersson, Torkel Glad och Lennart Ljung^[källa behövs]. Nämnas bör även den svenskfödde Harry Nyquist.

Se även

• Styrteknik
• Signalbehandling

Referenser

1. Glad och Ljung (2003). Reglerteori - Flervariabla och olinjära metoder. Torkel Glad, Lennart Ljung och Studentlitteratur. ISBN 978-91-44-03003-6 
2. ^ [ ] Glad och Ljung (2006). Reglerteknik - Grundläggande teori. Torkel Glad, Lennart Ljung och Studentlitteratur. ISBN 91-44-02275-1 
3. Industriell Reglerteknik Kurskompendium. Reglerteknik, Institutionen för systemteknik, Linköpings Universitet. 2012 
4. (på brittisk engelska) Modelling and Identification with Rational Orthogonal Basis Functions | SpringerLink. doi:10.1007/1-84628-178-4#section=532176&page=1. https://link.springer.com/book/10.1007/1-84628-178-4#section=532176&page=1. Läst 24 november 2017. 

Externa länkar

• Wikimedia Commons har media som rör Reglerteknik.
  Bilder & media
• Populärvetenskaplig beskrivning av ämnet
• Automation utifrån ett styrtekniskt perspektiv