Kolmogorovs axiom

Inom sannolikhetsteorin är Kolmogorovs axiom de tre axiom som entydigt bestämmer begreppet sannolikhetsfunktion. Sannolikhetsteorin axiomatiserades 1933 av den ryske matematikern A. Kolmogorov i det numera klassiska verket Foundations of the Theory of Probability.

Kolmogorovs tre axiom

En reell funktion ${\displaystyle P}$ på händelser i utfallsrummet ${\displaystyle \Omega }$ är en sannolikhetsfunktion om den uppfyller de tre nedanstående axiomen. En funktion som inte uppfyller dessa axiom är inte en sannolikhetsfunktion.

Första axiomet

Icke-negativitet

För en godtycklig händelse ${\displaystyle A\subseteq \Omega }$ gäller ${\displaystyle P(A)\in \mathbb {R} \land P(A)\geq 0}$.

Andra axiomet

Normalisering

För utfallsrummet ${\displaystyle \Omega }$ gäller ${\displaystyle P(\Omega )=1}$.

Tredje axiomet

Ändlig additivitet

Om utfallsrummet är ändligt och om ${\displaystyle A\cap B=\varnothing }$ så är

${\displaystyle P(A\cup B)=P(A)+P(B)}$.

Uppräknelig additivitet

Om utfallsrummet är oändligt så gäller för en oändlig följd av händelser ${\displaystyle A_{1},A_{2},...}$ om ${\displaystyle A_{i}\cap A_{j}=\varnothing }$ för alla ${\displaystyle i\neq j}$, att

${\displaystyle P(\bigcup _{i=1}^{\infty }A_{i})=\sum _{i=1}^{\infty }P(A_{i})}$.

Följdsatser

Monotonitet

Om ${\displaystyle A\subseteq B}$ gäller att ${\displaystyle P(A)\leq P(B)}$.

Bevis

${\displaystyle B}$ kan skrivas som ${\displaystyle A\lor B\backslash A}$ (A eller (B men inte A)). Det är enkelt att se att dessa två mängder är disjunkta och enligt Kolmogorovs tredje axiom får vi

${\displaystyle P(B)=P(A)+P(B\backslash A)}$

Högerledet består, enligt Kolmogorovs första axiom, av två positiva sannolikheter. Det är då tydligt att ${\displaystyle P(A)\leq P(B)}$.

Det numeriska intervallet

För en händelse ${\displaystyle A\subseteq \Omega }$ gäller ${\displaystyle 0\leq P(A)\leq 1}$

Bevis

Med monotonitetsegenskapen ovan får vi direkt ${\displaystyle P(A)\leq P(\Omega )=1}$ och tillsammans med Kolmogorovs första axiom följer påståendet.

Komplementsannolikheten

Sannolikheten för komplementhändelsen ${\displaystyle A^{\complement }}$ till ${\displaystyle A}$ är

${\displaystyle P(A^{\complement })=1-P(A)}$

Bevis

Antag att ${\displaystyle A\subseteq \Omega }$, då gäller att komplementhändelsen ${\displaystyle A^{\complement }\subseteq \Omega }$. Ett godtyckligt element ur ${\displaystyle \Omega }$ tillhör antingen ${\displaystyle A}$ eller ${\displaystyle A^{\complement }}$, det vill säga

${\displaystyle x\in \Omega \iff x\in A\cup A^{\complement }\Rightarrow \Omega =A\cup A^{\complement }}$.

Detta medför att

${\displaystyle P(\Omega )=P(A\cup A^{\complement })=1}$

Vi behöver nu bara konstatera att om ett element tillhör ${\displaystyle A}$ tillhör det inte ${\displaystyle A^{\complement }}$, vilket är innebörden av komplementhändelse. Mer formellt har vi

${\displaystyle x\in A\Rightarrow x\notin A^{\complement }}$

som leder till den logiska slutsatsen att

${\displaystyle A\cap A^{\complement }=\varnothing }$.

Kolmogorovs tredje axiom ger då

${\displaystyle P(A\cup A^{\complement })=P(A)+P(A^{\complement })=1\Rightarrow P(A^{\complement })=1-P(A)}$

Sannolikhetsteorins additionslag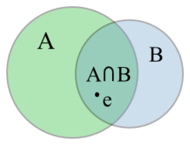

En händelse e som tillhör A ∩ B räknas två gånger i summan
P(A) + P(B) och i additionslagen kompenseras detta med termen
-P(A ∩ B)

För två händelser ${\displaystyle A}$ och ${\displaystyle B}$ gäller

${\displaystyle P(A\cup B)=P(A)+P(B)-P(A\cap B)}$

Bevis

Notera att mängden ${\displaystyle A\cup B}$ kan skrivas som ${\displaystyle A\cup (B\cap A^{\complement })}$. Detta inses enklast genom att tillämpa välkända mängdteoretiska räkneregler:

${\displaystyle A\cup (B\cap A^{\complement })=(A\cup B)\cap (A\cup A^{\complement })=(A\cup B)\cap \Omega =A\cup B}$

Då ${\displaystyle A}$ och ${\displaystyle A^{\complement }}$ är disjunkta händelser gäller att ${\displaystyle A}$ och ${\displaystyle B\cap A^{\complement }}$ är disjunkta händelser. Vi har alltså, från Kolmogorovs tredje axiom, att

${\displaystyle P(A\cup B)=P(A\cup (B\cap A^{\complement }))=P(A)+P(B\cap A^{\complement })\quad (1)}$

Genom att på liknande sätt skriva

${\displaystyle B=(B\cap A)\cup (B\cap A^{\complement })}$

och använda Kolmogorovs tredje axiom igen har vi

${\displaystyle P(B)=P((B\,\cap \,A)\,\cup \,(B\,\cap \,A^{\complement }))=}$

${\displaystyle P(B\,\cap \,A)+P(B\,\cap \,A^{\complement })\Rightarrow P(B)-P(B\,\cap \,A)=P(B\,\cap \,A^{\complement })\quad (2)}$

Om uttrycket ${\displaystyle P(B\cap \,A^{\complement })}$ från (2) sätts in i (1) erhålls

${\displaystyle P(A\cup B)=P(A)+P(B)-P(B\cap A)}$

Sannolikheten för den tomma mängden

${\displaystyle P(\varnothing )=0}$

Bevis

${\displaystyle \Omega \cap \varnothing =\varnothing \land \Omega \cup \varnothing =\Omega }$.

Enligt Kolmogorovs tredje axiom har vi

${\displaystyle P(\Omega \cup \varnothing )=P(\Omega )+P(\varnothing )=1\Rightarrow P(\varnothing )=0}$

Klassisk sannolikhetsdefinition

För ett slumpexperiment med ändligt utfallsrum ${\displaystyle \Omega }$ och likformig sannolikhetsfördelning gäller för en händelse ${\displaystyle A\subseteq \Omega }$ att

${\displaystyle P(A)=\mathrm {\frac {antalet\ gynnsamma\ utfall\ f{\ddot {o}}rA}{antalet\ m{\ddot {o}}jliga\ utfall}} =\mathrm {\frac {|A|}{|\Omega |}} }$

Bevis

Antag att ${\displaystyle \Omega }$ består av ${\displaystyle n}$ händelser ${\displaystyle a_{1},a_{2},...,a_{n}}$.

Enligt Kolmogorovs andra och tredje axiom gäller

${\displaystyle P(\Omega )=\sum _{i=1}^{n}P(a_{i})=1}$

Enligt antagandet om likformig sannolikhetsfördelning är alla händelser ${\displaystyle a_{i}}$ där ${\displaystyle i=1,2,...,n}$ lika sannolika, vilket ger

${\displaystyle \sum _{i=1}^{n}P(a_{i})=nP(a_{i})=1\Rightarrow P(a_{i})={\frac {1}{n}}}$

Därmed kan ${\displaystyle P(A)}$ beräknas:

${\displaystyle P(A)=\sum _{i:a_{i}\in A}P(a_{i})=\sum _{i:a_{i}\in A}{\frac {1}{n}}=|A|\cdot {\frac {1}{n}}={\frac {|A|}{n}}={\frac {|A|}{|\Omega |}}}$

Exempel

Problem om komplementsannolikhet

Sannolikheten att ett äpple faller på Isaac Newtons huvud uppskattas av honom själv till 0.0003. Vad är sannolikheten att äpplet inte faller?

För att lösa uppgiften genom att använda Kolmogorovs axiomsystem måste vi införa lämpliga beteckningar. Beteckna händelsen att äpplet faller på Isaac Newtons huvud med A. P(A) betyder då sannolikheten att äpplet faller på Newtons huvud. Enligt uppgiften är P(A) = 0.0003. Händelsen att äpplet inte faller kan betecknas ${\displaystyle A^{\complement }}$. Med hjälp av Kolmogorovs axiomsystem får vi sannolikheten att äpplet inte faller till

${\displaystyle P(A^{\complement })=1-P(A)=1-0.0003=0.9997}$.

Vad som inte är tydligt i lösningen av problemet är utfallsrummet ${\displaystyle \Omega }$. I typuppgifter som denna brukar man helt enkelt betrakta ${\displaystyle \Omega }$ som ${\displaystyle A\cup A^{\complement }}$.

Problem om sannolikhetsteorins additionslag

Sannolikheten för att antingen den ena eller den andra händelsen inträffar är 0.5, sannolikheten att den ena inträffar är 0.1 och sannolikheten att den andra inträffar är 0.2. Vad är sannolikheten att båda inträffar?

Beteckna den ena händelsen som ${\displaystyle A}$ och den andra som ${\displaystyle B}$. Från uppgiften har vi

${\displaystyle P(A\cup B)=0.5\quad P(A)=0.1\quad P(B)=0.2}$

Enligt Kolmogorovs axiomsystem (sannolikhetsteorins additionslag) gäller alltid att

${\displaystyle P(A\cup B)=P(A)+P(B)-P(B\cap A)}$

Vi sätter in de kända talen för att lösa ut det okända:

${\displaystyle 0.5=0.1+0.2-P(B\cap A)\Rightarrow P(B\cap A)=-0.2}$

Men enligt Kolmogorovs första axiom måste sannolikheten för en händelse vara större än noll. Alltså kan inte problemet lösas.

Problem om klassisk sannolikhetsdefinition

Åtta torn placeras slumpmässigt på ett schackbräde. Vad är sannolikheten att inget torn kan slå ett annat?

Låt ${\displaystyle A}$ beteckna händelsen att inget av de åtta tornen kan slå ett annat. Lösningen erhålls genom att beräkna ${\displaystyle |A|}$ och ${\displaystyle |\Omega |}$ och sedan tillämpa den klassiska sannolikhetsdefinitionen.

Utfallsrummet är de sätt som åtta torn kan placeras på ett schackbräde. Det första tornet kan placeras på 8⋅8 = 64 sätt, det andra på 64 - 1, det tredje på 64 - 2 sätt och så vidare till det åttonde tornet vilket kan placeras på 64 - 7 = 57 sätt. Enligt multiplikationsprincipen är därmed

${\displaystyle |\Omega |=64\cdot 63\cdots 56\cdot 57}$

För att beräkna ${\displaystyle |A|}$ noterar vi att första tornet kan placeras på 8⋅8 platser. När det andra tornet skall placeras är den rad och kolumn där det första tornet är placerat upptagna. De möjliga rutorna att placera det andra tornet på kan bilda ett bräde med 7 rader och 7 kolumner vilket ger 7⋅7 möjligheter. Nästa torn kan placeras på 6⋅6 sätt och så vidare till det åttonde tornet vilket kan placeras på 1⋅1 sätt. Enligt multiplikationsprincipen är då

${\displaystyle |A|=8^{2}\cdot 7^{2}\cdots 2^{2}\cdot 1^{2}}$

Den klassiska sannolikhetsdefinitionen kan nu användas för att beräkna den sökta sannolikheten:

${\displaystyle P(A)={\frac {|A|}{|\Omega |}}={\frac {8^{2}\cdot 7^{2}\cdots 2^{2}\cdot 1^{2}}{64\cdot 63\cdots 56\cdot 57}}\approx 9.11\cdot 10^{-6}}$

Således är sannolikheten att inget av de åtta tornen kan slå ett annat ungefär 9 på miljonen.

Se även

• Sannolikhetsteori
• Mängdteori
• Axiom
• Matematiskt bevis

Källor

• Stokastik av Sven Erick Alm, Tom Britton, 20011, sida 10.

Externa länkar

• Kolmogorov's Axioms, Wolfram MathWorld.
• Kolmogorov`s probability calculus, Stanford Encyclopedia of Philosophy.