|
Banlutning Banlutningen eller inklinationen, betecknat ι, är vinkeln mellan ett objekts omloppsbana och ett referensplan. För satellitbanor är referensen jordens ekvatorialplan, för en planetbana är referensen ekliptikan. Det allmänna fallet för en cirkulär bana är att den lutar och tillbringar halva banan över norra halvklotet och andra halvan över södra. Om banan pendlar mellan 20° nordlig latitud och 20° sydlig latitud, är dess banlutning 20°. BanorLutningen är ett av de sex banelement som beskriver en banas form och orientering på himlavalvet. Det är vinkeln mellan omloppsplanet och referensplanet, normalt angivet i grader. För en satellit som kretsar kring en planet är referensplanet vanligtvis det plan som innehåller planetens ekvator. För planeter i solsystemet är referensplanet vanligtvis ekliptikan, det plan där jorden kretsar kring solen.[1][2] Detta referensplan är mest praktiskt för jordbaserade observatörer. Därför är jordens banlutning per definition noll. Lutning kan istället mätas med avseende på ett annat plan, såsom solens ekvator eller det oföränderliga planet (planet som representerar solsystemets rörelsemängdsmoment, ungefär Jupiters omloppsplan). Naturliga och artificiella satelliterNaturliga eller artificiella satelliters banlutning mäts i förhållande till ekvatorialplanet hos kroppen de kretsar kring, om de kretsar tillräckligt nära. Ekvatorialplanet är planet vinkelrätt mot mittkroppens rotationsaxel. En lutning på 30° kan också beskrivas med en vinkel på 150°. Konventionen är att den normala banan är prograd – en bana i samma riktning som planeten roterar. Lutningar större än 90° beskriver retrograda banor (bakåt). Sålunda:
För nedslagsgenererade månar till jordlika planeter ganska nära sin stjärna, med ett stort avstånd mellan planet och måne, tenderar månarnas omloppsplan att vara i linje med planetens bana runt stjärnan – på grund av tidvatteneffekt från stjärnan. Om avståndet mellan planet och månen är litet kan dock banplanet luta. För gasjättar tenderar månarnas banor att vara i linje med jätteplanetens ekvator, eftersom månarna bildades i cirkumplanetära skivor.[4] Strängt taget gäller detta endast vanliga satelliter. Infångade kroppar på avlägsna banor varierar mycket i sina lutningar, medan infångade kroppar i relativt nära banor tenderar att ha låga lutningar på grund av tidvatteneffekter och störningar från stora månar. Exoplaneter och flerstjärnsystemFör exoplaneter eller medlemmar av multipelstjärnor mäts vinkeln på banans plan i förhållande till planet vinkelrätt mot siktlinjen från jorden till objektet.[5]
Eftersom ordet "lutning" används i exoplanetstudier för denna siktlinjelutning, uttrycks vinkeln mellan planetens bana och dess stjärnas rotationsaxel med termen "spin-orbit angle" eller "spin-orbit alignment".[5] I de flesta fall är orienteringen av stjärnans rotationsaxel okänd. Eftersom radialhastighetsmetoden lättare hittar planeter med banor närmare kanten, har de flesta exoplaneter som hittas med denna metod lutningar mellan 45° och 135°, även om lutningen i de flesta fall inte är känd. Följaktligen har de flesta exoplaneter som hittas genom mätning av radiell hastighet faktiska massor som inte är mer än 40 procent större än deras minsta massor. Om banan är nästan ansikte mot ansikte, särskilt för en superjupiter som upptäcks genom mätning av radiell hastighet, kan dessa objekt faktiskt vara bruna dvärgar eller till och med röda dvärgar. Ett särskilt exempel är HD 33636 B, som har en sann massa på 142 MJ, motsvarande en stjärna av spektralklass M6 V, medan dess minsta massa var 9,28 MJ. Om banan är nästan sedd från kanten, kan planeten ses passera dess stjärna. Beräkning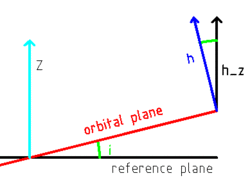 I astrodynamiken kan lutningen beräknas från orbital momentumvektorn (eller någon vektor vinkelrätt mot omloppsplanet) som där är z-komponenten av . Ömsesidig lutning av två banor kan beräknas från deras respektive lutning mot ett annat plan med hjälp av cosinusregel för vinklar. Observationer och teorierDe flesta planetbanor i solsystemet har relativt små lutningar, både i förhållande till varandra och till solens ekvator. Å andra sidan har dvärgplaneterna Pluto och Eris banlutningar mot ekliptikan på 17° respektive 44°, och banan för den stora asteroiden Pallas lutar 34°. År 1966 publicerade Peter Goldreich en klassisk rapport om utvecklingen av månens bana och om andra månars banor i solsystemet.[6] Han visade att det för varje planet finns ett avstånd så att månar närmare planeten än det avståndet upprätthåller en nästan konstant omloppslutning i förhållande till planetens ekvator (med en orbital precession främst på grund av planetens tidvattenpåverkan), medan månar längre bort upprätthåller en nästan konstant omloppslutning i förhållande till ekliptikan (med precession som främst beror på solens tidvattenpåverkan). Månarna i den första kategorin, med undantag för Neptunus måne Triton, kretsar nära ekvatorialplanet. Han drog slutsatsen att dessa månar bildades av ekvatoriella ackretionsskivor. Men han fann att vår måne, även om den en gång var inne i det kritiska avståndet från jorden, aldrig hade en ekvatorial bana som man kunde förvänta sig från olika scenarier för dess ursprung. Detta kallas månens lutningsproblem, som man sedan dess har föreslagit olika möjliga lösningar för.[7] Se ävenReferenser
Noter
Externa länkar
|
||||||||||||||||||||||||||||||||||
Portal di Ensiklopedia Dunia



