|
Четырёхзвенный механизмЧетырёхзве́нный механи́зм — простейший кинематически замкнутый механизм, звенья которого способны двигаться друг относительно друга. Этот механизм состоит из четырёх звеньев, каждое из которых соединено подвижными соединениями с двумя другими. Такие механизмы широко используются в машиностроении и других областях техники. При изучении раздела «Кинематика» в курсе теоретической механики четырёхзвенный механизм выступает в качестве важнейшей модели, которая служит для иллюстрации теоретических закономерностей и отработки основных алгоритмов расчёта. ТипыПлоскийЕсли каждое соединение звеньев имеет лишь одну вращательную степень свободы, то такой механизм обычно является плоским и в этом случае называется шарнирным четырёхзвенником[1]. В данном случае можно определить конфигурацию всего механизма, если известны конфигурации любых двух из этих звеньев. Как правило, одно из звеньев механизма обычно на протяжении всего времени движения остаётся неподвижным (такое звено называется стойкой, основанием или рамой), так что для определения конфигурации механизма фактически достаточно найти конфигурацию лишь одного из оставшихся звеньев. Те два звена четырёхзвенного механизма, которые соединены с основанием, называются основными звеньями; если основное звено способно по отношению к стойке совершать полный оборот, то его именуют кривошипом, иначе — коромыслом[1]. Оставшееся звено, которое соединяет между собой основные звенья и не связано непосредственно с основанием, носит название шатуна. То из основных звеньев, к которому приложено внешнее силовое воздействие, называют ведущим звеном. Другое основное звено является ведомым, и его движение (как, впрочем, и движение шатуна) полностью задаётся движением входного звена. 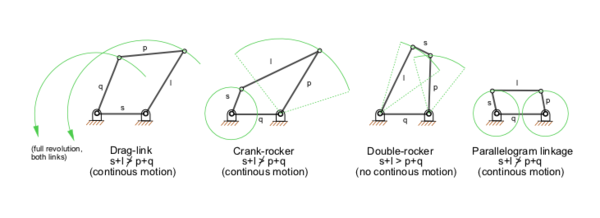 Плоские четырёхзвенные механизмы применяют для многих случаев преобразования одного вида движения в другое. Но, как правило, они используются для преобразования вращательного движения в качательное (реже наоборот) или равномерного вращательного в неравномерное вращательное. Кинематический анализ плоского четырёхзвенного механизма намного проще, чем анализ большинства других механизмов, более сложных, что способствует популярности таких механизмов. Для шарнирного четырёхзвенника справедлив следующий закон (теорема Грасгофа о шарнирном четырёхзвеннике):
 На рис. 1 приведены различные случаи четырёхзвенного механизма с неподвижным основанием. К числу плоских четырёхзвенных механизмов относятся также четырёхзвенные кривошипно-ползунный и кулисный механизмы[2]. ПространственныйК числу пространственных четырёхзвенных механизмов относятся показанные справа сферический шарнирный четырёхзвенник[3] и механизм Беннета[4] — четырёхзвенный пространственный механизм с вращательными кинематическими парами, изобретённый в 1903 г. английским математиком и механиком Дж. Беннетом (Geoffrey Thomas Bennett)[5].  ПрименениеОдним из примеров применения четырёхзвенного механизма является пантограф, имеющий четыре звена и две степени свободы, т. е. только одну фиксированную точку. Другой пример применения — механизм Чебышёва.  КинематикаСм. такжеПримечания
Литература
Ссылки
|

