Сферичность

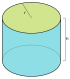
Схематичное представление различия форм частиц. Показаны два параметра: сферичность (чем выше объект, тем больше сферичность) и круглость (чем правее объект, тем больше круглость).

Сфери́чность — количественная мера того, насколько сферическим (круглым) является объект.

Определённая Х. Уоделлом (H. Wadell) в 1935 году[1] сферичность ${\displaystyle \Psi }$ частицы представляет собой отношение площади поверхности сферы (того же объёма, что и данная частица) к площади поверхности частицы:

${\displaystyle \Psi ={\frac {\pi ^{\frac {1}{3}}(6V_{p})^{\frac {2}{3}}}{A_{p}}},}$

где ${\displaystyle V_{p}}$ равно объёму частицы и ${\displaystyle A_{p}}$ равно площади поверхности частицы. Сферичность сферы равна единице по определению, а вследствие изопериметрического неравенства сферичность любого другого тела меньше единицы.

Вывод формулы

Хакон Уоделл определил сферичность как отношение площади поверхности сферы равного с данной частицей объёма к площади поверхности данной частицы. Рассмотрим сначала сферическую частицу, у которой площадь поверхности ${\displaystyle A_{s}}$, а её объём ${\displaystyle V_{p}}$ равен объёму исследуемой частицы.

Выразим площадь поверхности этой частицы ${\displaystyle A_{s}}$ через её объём ${\displaystyle V_{p}}$:

${\displaystyle A_{s}^{3}=\left(4\pi r^{2}\right)^{3}=4^{3}\pi ^{3}r^{6}=4\pi \left(4^{2}\pi ^{2}r^{6}\right)=4\pi \cdot 3^{2}\left({\frac {4^{2}\pi ^{2}}{3^{2}}}r^{6}\right)=36\pi \left({\frac {4\pi }{3}}r^{3}\right)^{2}=36\,\pi V_{p}^{2}.}$

Следовательно,

${\displaystyle A_{s}=\left(36\,\pi V_{p}^{2}\right)^{\frac {1}{3}}=36^{\frac {1}{3}}\pi ^{\frac {1}{3}}V_{p}^{\frac {2}{3}}=6^{\frac {2}{3}}\pi ^{\frac {1}{3}}V_{p}^{\frac {2}{3}}=\pi ^{\frac {1}{3}}\left(6V_{p}\right)^{\frac {2}{3}}.}$

Тогда выражение сферичности ${\displaystyle \Psi }$ для произвольной частицы, имеющей площадь поверхности ${\displaystyle A_{p}}$ и объём ${\displaystyle V_{p}}$, приобретает вид

${\displaystyle \Psi ={\frac {A_{s}}{A_{p}}}={\frac {\pi ^{\frac {1}{3}}\left(6V_{p}\right)^{\frac {2}{3}}}{A_{p}}}.}$

Примеры

Эллипсоидальные объекты

Сферичность ${\displaystyle \Psi }$ сплюснутого сфероида равна

${\displaystyle \Psi ={\frac {\pi ^{\frac {1}{3}}(6V_{p})^{\frac {2}{3}}}{A_{p}}}={\frac {2{\sqrt[{3}]{ab^{2}}}}{a+{\frac {b^{2}}{\sqrt {a^{2}-b^{2}}}}\ln {\left({\frac {a+{\sqrt {a^{2}-b^{2}}}}{b}}\right)}}},}$

где a и b равны большой и малой полуосям сфероида.

Сферичность некоторых объектов

Название	Рисунок	Объём	Площадь поверхности	Сферичность
Платоновы тела
Тетраэдр		${\displaystyle {\frac {\sqrt {2}}{12}}\,s^{3}}$	${\displaystyle {\sqrt {3}}\,s^{2}}$	${\displaystyle \left({\frac {\pi }{6{\sqrt {3}}}}\right)^{\frac {1}{3}}\approx 0.671}$
Куб (гексаэдр)		${\displaystyle \,s^{3}}$	${\displaystyle 6\,s^{2}}$	${\displaystyle \left({\frac {\pi }{6}}\right)^{\frac {1}{3}}\approx 0.806}$
Октаэдр		${\displaystyle {\frac {1}{3}}{\sqrt {2}}\,s^{3}}$	${\displaystyle 2{\sqrt {3}}\,s^{2}}$	${\displaystyle \left({\frac {\pi }{3{\sqrt {3}}}}\right)^{\frac {1}{3}}\approx 0.846}$
Додекаэдр		${\displaystyle {\frac {1}{4}}\left(15+7{\sqrt {5}}\right)\,s^{3}}$	${\displaystyle 3{\sqrt {25+10{\sqrt {5}}}}\,s^{2}}$	${\displaystyle \left({\frac {\left(15+7{\sqrt {5}}\right)^{2}\pi }{12\left(25+10{\sqrt {5}}\right)^{\frac {3}{2}}}}\right)^{\frac {1}{3}}\approx 0.910}$
Икосаэдр		${\displaystyle {\frac {5}{12}}\left(3+{\sqrt {5}}\right)\,s^{3}}$	${\displaystyle 5{\sqrt {3}}\,s^{2}}$	${\displaystyle \left({\frac {\left(3+{\sqrt {5}}\right)^{2}\pi }{60{\sqrt {3}}}}\right)^{\frac {1}{3}}\approx 0.939}$
Тела с осевой симметрией
Конус ${\displaystyle (h=2{\sqrt {2}}r)}$		${\displaystyle {\frac {1}{3}}\pi \,r^{2}h}$ ${\displaystyle ={\frac {2{\sqrt {2}}}{3}}\pi \,r^{3}}$	${\displaystyle \pi \,r(r+{\sqrt {r^{2}+h^{2}}})}$ ${\displaystyle =4\pi \,r^{2}}$	${\displaystyle \left({\frac {1}{2}}\right)^{\frac {1}{3}}\approx 0.794}$
Полусфера		${\displaystyle {\frac {2}{3}}\pi \,r^{3}}$	${\displaystyle 3\pi \,r^{2}}$	${\displaystyle \left({\frac {16}{27}}\right)^{\frac {1}{3}}\approx 0.840}$
Цилиндр ${\displaystyle (h=2\,r)}$		${\displaystyle \pi r^{2}h=2\pi \,r^{3}}$	${\displaystyle 2\pi r(r+h)=6\pi \,r^{2}}$	${\displaystyle \left({\frac {2}{3}}\right)^{\frac {1}{3}}\approx 0.874}$
Тор ${\displaystyle (R=r)}$		${\displaystyle 2\pi ^{2}Rr^{2}=2\pi ^{2}\,r^{3}}$	${\displaystyle 4\pi ^{2}Rr=4\pi ^{2}\,r^{2}}$	${\displaystyle \left({\frac {9}{4\pi }}\right)^{\frac {1}{3}}\approx 0.894}$
Сфера		${\displaystyle {\frac {4}{3}}\pi r^{3}}$	${\displaystyle 4\pi \,r^{2}}$	${\displaystyle 1\,}$

См. также

• Изопериметрическое отношение

Примечания

1. Wadell, Hakon. Volume, Shape and Roundness of Quartz Particles (англ.) // Journal of Geology^[англ.] : journal. — 1935. — Vol. 43, no. 3. — P. 250—280. — doi:10.1086/624298.