Гиперболоид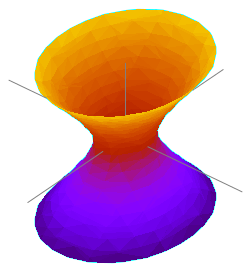   Гиперболо́ид (от др.-греч. ὑπερβολή — гипербола, и εἶδος — вид, внешность) — незамкнутая центральная поверхность второго порядка в трёхмерном пространстве, задаваемая в декартовых координатах уравнением
где a и b — действительные полуоси, а c — мнимая полуось; или
где a и b — мнимые полуоси, а c — действительная полуось. [1] Если a = b, то такая поверхность называется гиперболоидом вращения. Однополостный гиперболоид вращения может быть получен вращением гиперболы вокруг её мнимой оси, двуполостный — вокруг действительной. Двуполостный гиперболоид вращения также является геометрическим местом точек P, модуль разности расстояний от которых до двух заданных точек A и B постоянен: . В этом случае A и B называются фокусами гиперболоида.[2] Однополостный гиперболоид является дважды линейчатой поверхностью; если он является гиперболоидом вращения, то он может быть получен вращением прямой вокруг другой прямой, скрещивающейся с ней. В науке и техникеСвойство двуполостного гиперболоида вращения отражать лучи, направленные в один из фокусов, в другой фокус, используется в телескопах системы Кассегрена и в антеннах Кассегрена. Галерея
В искусствеВ архитектуреЛинейчатая конструкция, имеющая форму однополостного гиперболоида, является жёсткой: если балки соединить шарнирно, гиперболоидная конструкция всё равно будет сохранять свою форму под действием внешних сил. Для высоких сооружений основную опасность несёт ветровая нагрузка, а у решётчатой конструкции она невелика. Эти особенности делают гиперболоидные конструкции прочными, несмотря на невысокую материалоёмкость. Примерами гиперболоидных конструкций являются:
В литературе
См. также
Примечания
Литература
Ссылки
|
Portal di Ensiklopedia Dunia


















