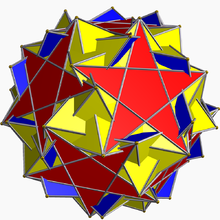
Dodecadodecaedru snub inversat
În geometrie dodecadodecaedrul snub inversat este un poliedru stelat uniform , cu indicele U60 . Are 84 de fețe (60 triunghiuri , 12 pentagoane și 12 pentagrame ), 150 de laturi și 60 de vârfuri .[ 1] [ 2]
Este reprezentat prin diagrama Coxeter–Dynkin simbolul Wythoff | 5/3 2 5[ 1] simbolul Schläfli sr{5/3,5}.
Coordonate carteziene
coordonatele carteziene ale vârfurilor sunt toate permutările pare cu un număr par de semne plus ale
(
±
2
α
,
±
2
,
±
2
β
)
{\displaystyle \left(\,\pm 2\alpha ,\,\pm 2,\,\pm 2\beta \,\right)}
(
±
(
α
+
β
φ
−
1
+
φ
)
,
±
(
−
α
φ
+
β
+
φ
−
1
)
,
±
(
α
φ
−
1
+
β
φ
−
1
)
)
{\displaystyle \left(\,\pm (\alpha +\beta \varphi ^{-1}+\varphi ),\,\pm (-\alpha \varphi +\beta +\varphi ^{-1}),\,\pm (\alpha \varphi ^{-1}+\beta \varphi -1)\,\right)}
(
±
(
−
α
φ
−
1
+
β
φ
+
1
)
,
±
(
−
α
+
β
φ
−
1
−
φ
)
,
±
(
α
φ
+
β
−
φ
−
1
)
)
{\displaystyle \left(\,\pm (-\alpha \varphi ^{-1}+\beta \varphi +1),\,\pm (-\alpha +\beta \varphi ^{-1}-\varphi ),\,\pm (\alpha \varphi +\beta -\varphi ^{-1})\,\right)}
(
±
(
−
α
φ
−
1
+
β
φ
−
1
)
,
±
(
α
−
β
φ
−
1
−
φ
)
,
±
(
α
φ
+
β
+
φ
−
1
)
)
{\displaystyle \left(\,\pm (-\alpha \varphi ^{-1}+\beta \varphi -1),\,\pm (\alpha -\beta \varphi ^{-1}-\varphi ),\,\pm (\alpha \varphi +\beta +\varphi ^{-1})\,\right)}
(
±
(
α
+
β
φ
−
1
−
φ
)
,
±
(
α
φ
−
β
+
φ
−
1
)
,
±
(
α
φ
−
1
+
β
φ
+
1
)
)
{\displaystyle \left(\,\pm (\alpha +\beta \varphi ^{-1}-\varphi ),\,\pm (\alpha \varphi -\beta +\varphi ^{-1}),\,\pm (\alpha \varphi ^{-1}+\beta \varphi +1)\,\right)}
unde
φ
=
1
+
5
2
{\displaystyle \varphi ={\frac {1+{\sqrt {5}}}{2}}}
secțiunea de aur ,
α
{\displaystyle \alpha }
rădăcina reală negativă a polinomului
φ
α
4
−
α
3
+
2
α
2
−
α
−
φ
−
1
,
≈
−
0
,
3352090
,
{\displaystyle \varphi \alpha ^{4}-\alpha ^{3}+2\alpha ^{2}-\alpha -\varphi ^{-1},\,\approx -0,3352090,}
[ 3]
β
=
α
2
φ
−
1
+
φ
α
φ
−
φ
−
1
.
{\displaystyle \beta ={\frac {\alpha ^{2}\varphi ^{-1}+\varphi }{\alpha \varphi -\varphi ^{-1}}}.}
Permutările impare ale coordonatelor de mai sus cu un număr impar de semne plus dau o altă formă, enantiomorfă a celeilalte.[ 4]
Raza circumscrisă pentru lungimea laturii de 1 unitate ,
R
=
0
,
8516302
{\displaystyle R=0,8516302}
[ 2] [ 5]
64
R
8
−
192
R
6
+
180
R
4
−
65
R
2
+
8.
{\displaystyle 64R^{8}-192R^{6}+180R^{4}-65R^{2}+8.}
Volum
Volumul său, V , este dat de cea mai mică dintre rădăcinile reale ale polinomului de gradul al patrulea în
x
2
{\displaystyle x^{2}}
[ 6]
64
x
8
−
21440
x
6
+
18100
x
4
+
5895625
x
2
+
60062500.
{\displaystyle 64x^{8}-21440x^{6}+18100x^{4}+5895625x^{2}+60062500.}
Ca urmare, volumul este
V
≈
4
,
61431
a
3
{\displaystyle V\approx 4,61431~a^{3}}
unde a este lungimea laturilor tuturor poligoanelor (care sunt regulate).
Polinoamele de mai sus definesc și raza circumscrisă și volumul dodecadodecaedrului snub .
Dual: hexacontaedru pentagonal medial inversat
Poliedru dual
Dualul său este hexacontaedrul pentagonal medial inversat .[ 7] [ 8]
Note
^ a b c d e en Roman, Maeder. „60: inverted snub dodecadodecahedron” . MathConsult . Accesat în 23 octombrie 2023 .
^ a b en Eric W. Weisstein , Inverted Snub Dodecadodecahedron MathWorld .
^ en equation solver , wolframalpha.com, accesat 2023-10-23^ en Skilling, John (1975 ), „The complete set of uniform polyhedra”, Philosophical Transactions of the Royal Society A , 278 (1278): 111–135, doi :10.1098/rsta.1975.0022 ^ en equation solver , wolframalpha.com, accesat 2023-10-23^ en equation solver , wolframalpha.com, accesat 2023-10-23^ en Eric W. Weisstein , Medial Inverted Pentagonal Hexecontahedron MathWorld .^ en Wenninger, Magnus (1983 ), Dual Models , Cambridge University Press , doi :10.1017/CBO9780511569371 , ISBN 978-0-521-54325-5 , MR 0730208