|
Problema de Monty Hall
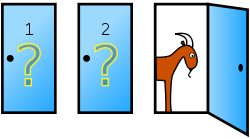 O problema de Monty Hall, também conhecido por paradoxo de Monty Hall, é um problema matemático e paradoxo que surgiu a partir de um concurso televisivo dos Estados Unidos chamado Let’s Make a Deal, exibido na década de 1970. O jogo consistia no seguinte: Monty Hall, o apresentador, apresentava três portas aos concorrentes. Atrás de uma delas estava um prêmio (um carro) e, atrás das outras duas, dois bodes.
Qual é a estratégia mais lógica? Ficar com a porta escolhida inicialmente ou mudar de porta? Com qual das duas portas ainda fechadas o concorrente tem mais probabilidades de ganhar? Por quê? Na realidade não é assim tão indiferente mudar ou ficar com a primeira escolha. No início, quando se escolheu uma das portas, havia 1/3 de probabilidade de ganhar o carro. Não existe razão aparente para essa probabilidade mudar após Monty Hall ter aberto uma das portas que não era premiada. As outras duas portas não escolhidas tinham em conjunto 2/3 de probabilidade de ocultarem o carro, e quando uma dessas portas é aberta (por não ter prêmio) a porta não escolhida que continua fechada passa a ter 2/3 de probabilidade de ser a porta do carro. A confusão é feita seguindo o raciocínio que parece mais lógico: "mas a porta escolhida também continua fechada... então cada uma das portas fechadas passa a ter 1/2 de chance de ter o carro?". O problemaO problema é muito mais complexo do que parece, e tornou-se famoso nos EUA como o problema de Monty Hall, devido ao apresentador que possuía um quadro bem similar (ou o contrário seria mais apropriado) em seu programa popular 'Let's Make a Deal' ['Vamos fazer um trato'] nos anos 70, algo como os diversos programas de auditório que ficaram famosos no Brasil com o apresentador Silvio Santos. A resposta intuitiva, porém erradaA resposta intuitiva ao problema é a que quando o apresentador revelou uma das portas não-premiadas, o concorrente passaria a ter à frente um novo dilema, com apenas duas portas e um prêmio, portanto as chances do prêmio estar em qualquer uma das duas portas passaria a ser de 50%. O apresentador teria ajudado o concorrente, já que as chances para acertar subiram de 33,33% para 50%, no entanto não faria diferença trocar ou não de porta, uma vez que ambas teriam as mesmas chances em 50% de possuírem o prêmio. No entanto, esta análise intuitiva é errada, pois a porta que o apresentador abre depende da porta que o concorrente escolheu inicialmente. O apresentador sabe desde o começo onde está o prêmio e assim ele nunca abrirá uma porta premiada. Ao abrir uma porta não premiada, ele não está criando um jogo novo, mas está dando informações valiosas ao concorrente sobre a localização do prêmio definida no jogo inicial. É por isso que a resposta é tão contra-intuitiva: parece-nos que o apresentador abriu uma porta aleatoriamente, mas isso está longe da verdade. Como se observa, se o concorrente tiver escolhido inicialmente uma porta não-premiada (as chances de isto acontecer são maiores do que acertar logo à primeira na porta premiada), o apresentador não tem liberdade de escolha e só pode abrir a porta não premiada que lhe resta, obrigando-o a continuar mantendo fechada a única porta premiada. A soluçãoA resposta correta e contra-intuitiva é que é vantajoso trocar. Na verdade, é mais provável estatísticamente ganhar o prêmio se trocar de porta do que se não o fizer, pois a probabilidade em acertar na premiada passa para o dobro, de 33,33% para 66,66%. Existem três portas - A, B e C. Quando o concorrente escolheu uma delas, digamos a A, a chance de que ela seja a premiada é de 1/3. Como consequência, a probabilidade de que tenha errado, ou em outras palavras, de que o prêmio esteja nas outras duas portas B ou C é de 2/3. Pode-se comprovar isso somando a probabilidade de cada uma das outras portas ou simplesmente sabendo que a probabilidade de que haja um prêmio é sempre 1. O importante é ter em mente que a chance de o prêmio estar nas outras portas que você não escolheu é de 2/3. Entendendo isso, basta ver que o apresentador abrirá sem erro uma dessas outras duas portas que contém um prémio mau, digamos que seja a B. Ao fazer isso, ele está lhe dando uma informação valiosa: se o prêmio estava nas outras portas que não escolheu (B ou C), então agora ele só pode estar na porta que você não escolheu e não foi aberta, ou seja, a porta C. Ou seja, se o concorrente errou ao escolher uma porta - e as chances disto são de 2/3 - então ao abrir uma das outras portas não-premiadas o apresentador está lhe dizendo onde está o prêmio. Toda vez que o concorrente tiver escolhido inicialmente uma porta errada, ao trocar de porta irá com mais probabilidade ganhar. Como as chances de que tenha errado em sua escolha inicial são de 2/3, se trocar suas chances de ganhar serão de 2/3 - e por conseguinte a chance de que ganhe se não trocar de porta é de apenas 1/3. É assim mais vantajoso trocar sempre de porta. A análise pode ser ilustrada em termos da chances de probabilidades iguais que o jogador inicialmente escolheu o carro, bode A, ou bode B (Economist 1999): O problema de Monty Hall é exposto em muitos cursos de probabilidades e de estatística, e um exercício com ele seria dado em Harvard e Princeton. Ele demonstra muito bem como nosso cérebro não foi feito para lidar intuitivamente com tais tipos específicos de problemas. Felizmente pode-se resolver o problema de Monty Hall no papel de forma simples e sem erro usando o teorema de Bayes relativo às probabilidades condicionadas. Bibliografia
Ver também |
Portal di Ensiklopedia Dunia





