Distribuição de Weibull

Em probabilidade e estatística a distribuição de Weibull é uma distribuição de probabilidade contínua. É nomeada devido a Waloddi Weibull que em 1951 lançou um artigo descrevendo a distribuição em detalhes e propondo diversas aplicações[1]. O campo de aplicações da distribuição de Weibull é vasto e abrange praticamente todas as áreas da ciência. Usando essa distribuição, realizou-se a modelagem bem sucedida de dados provenientes de grandes áreas de ciências física, biológica, social, saúde, ambiental e métodos baseados nesta distribuição são ferramentas indispensáveis para profissionais da engenharia de confiabilidade. Em geral, suas aplicações visam a determinação do tempo de vida médio e da taxa de falhas em função do tempo da população analisada. É também de grande interesse para estatísticos devido a suas diversas características específicas. O sucesso da distribuição se justifica não só pela sua eficácia, mas também ao fato de existirem recursos gráficos que facilitam sua interpretação e por ser capaz de fazer previsões de acurácia razoável mesmo quando a quantidade de dados disponível é baixa.

Definição

Uma variável aleatória x segue a distribuição de Weibull se sua função densidade de probabilidade é dada por[2]

${\displaystyle f(x;\lambda ,k)={\begin{cases}{\frac {k}{\lambda }}\left({\frac {x}{\lambda }}\right)^{k-1}e^{-(x/\lambda )^{k}}&x\geq 0,\\0&x<0.\end{cases}}}$

O parâmetro λ está definido de 0 a +${\displaystyle \infty }$ e é medido na mesma unidade que x. Se x tem unidade de tempo λ é denominado tempo característico pois a função de distribuição acumulada de qualquer distribuição de Weibull com parâmetros λ idênticos e k livre terá o valor de 0.6321 no ponto x=λ. Isso significa que a chance de sobrevivência de x por λ unidades de tempo é aproximadamente 63.21% independentemente do valor de k. Do ponto de vista estatístico λ é determinado parâmetro de escala pois variações no seu valor enquanto k é mantido constante causam a compressão ou expansão do gráfico.

Distribuição de Weibull para diferentes parâmetros de escala.

O parâmetro k está definido de 0 a +${\displaystyle \infty }$ e é adimensional. É chamado de declividade de Weibull pois determina a declividade da função de distribuição acumulada plotada em um papel de probabilidade Weibull. Do ponto de vista estatístico k é o parâmetro de forma. Variações no valor de k alteram drasticamente o comportamento da distribuição. Para k<1, o fator exponencial da distribuição é predominante e a curva fica em um formato de J e para k=1 a distribuição se reduz a uma distribuição exponencial. Para k>1 o fator polinomial da distribuição é predominante.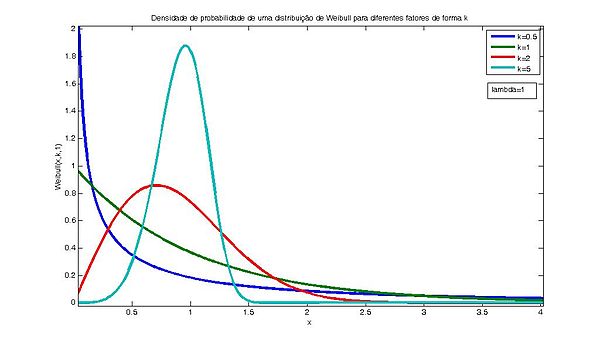

Distribuição de Weibull para diferentes parâmetros de forma.

Essa é distribuição de Weibull com 2 parâmetros. Existem outras definições com mais ou menos parâmetros dependendo da finalidade, veja relação com outras distribuições para outras formas.

Propriedades

Função densidade

A forma da função densidade da distribuição de Weibull muda drasticamente com o valor de k. Para 0 < k < 1, a função densidade tende a ${\displaystyle \infty }$ quando x se aproxima de zero por cima e é estritamente decrescente. Para k = 1, a função densidade tende a 1/λ quando x se aproxima de zero por cima, aumenta até seu modo e diminui depois disso. É interessante notar que a função densidade tem uma declividade infinitamente negativa em x = 0 se 0 < k < 1, declividade infinitamente positiva em x = 0 se 1 < k < 2 e declividade nula em x = 0 se k > 2. Para k = 2 a função densidade tem uma declividade finita e positiva em x = 0. Quando k tende ao infinito, a distribuição de Weibull converge para uma distribuição delta de Dirac centrada em x = λ. Além disso, a obliquidade e o coeficiente de variação dependem apenas do parâmetro de forma.

Função de distribuição

A função distribuição acumulada da distribuição de Weibull é

${\displaystyle F(x;k,\lambda )=1-e^{-(x/\lambda )^{k}}\,}$

para x ≥ 0, e F(x; k; λ) = 0 para x < 0.

O quantil da distribuição de Weibull é

${\displaystyle Q(p;k,\lambda )=\lambda {(-ln(1-p))}^{1/k}}$

para 0 ≤ p < 1.

A função hazard h (taxa de falhas) é dada por

${\displaystyle h(x;k,\lambda )={k \over \lambda }\left({x \over \lambda }\right)^{k-1}.}$

No contexto em que x é interpretado como o "tempo transcorrido até falha" a distribuição de Weibull fornece a distribuição de probabilidades de um dispositivo ou material falhar em um dado intervalo de tempo. Como pode ser visto na definição da função hazard h, existe uma dependência exponencial com o parâmetro k o que determina 3 comportamentos bem diferentes para:

• k<1: alta taxa de falha no início. Esse é um comportamento típico de processos industriais em que a maioria das falhas ocorre no processo de produção dos items ou quando a taxa de falha diminui com a eliminação da população defeituosa de dispositivos.
• k=1: chance de falha independente do tempo e comportamento exponencialmente decrescente da distribuição. Processos "sem memória" em que as falhas ocorrem devido a razões aleatórias.
• k>1: chance de falha crescente com o tempo. Casos em que há um processo de envelhecimento.

Momentos

A função geradora de momentos do logaritmo de uma variável aleatória que se distribui conforme uma distribuição de Weibull é dada por[3]

${\displaystyle E\left[e^{t\log X}\right]=\lambda ^{t}\Gamma \left({\frac {t}{k}}+1\right)}$

onde Γ é a função gama. Similarmente, a função característica^[desambiguação necessária] de log X é dada por

${\displaystyle E\left[e^{it\log X}\right]=\lambda ^{it}\Gamma \left({\frac {it}{k}}+1\right).}$

Em particular, o enésimo momento de X é dado por

${\displaystyle m_{n}=\lambda ^{n}\Gamma \left(1+{\frac {n}{k}}\right).}$

A média e a variância de uma variável aleatória seguindo a distribuição de Weibull podem ser expressas como

${\displaystyle \mathrm {E} (X)=\lambda \Gamma \left(1+{\frac {1}{k}}\right)\,}$

e

${\displaystyle {\textrm {var}}(X)=\lambda ^{2}\left[\Gamma \left(1+{\frac {2}{k}}\right)-\left(\Gamma \left(1+{\frac {1}{k}}\right)\right)^{2}\right]\,.}$

A obliquidade é dada por

${\displaystyle \gamma _{1}={\frac {\Gamma \left(1+{\frac {3}{k}}\right)\lambda ^{3}-3\mu \sigma ^{2}-\mu ^{3}}{\sigma ^{3}}}}$

onde a média é denotada por μ e o desvio padrão por σ.

A curtose em excesso é dada por

${\displaystyle \gamma _{2}={\frac {-6\Gamma _{1}^{4}+12\Gamma _{1}^{2}\Gamma _{2}-3\Gamma _{2}^{2}-4\Gamma _{1}\Gamma _{3}+\Gamma _{4}}{[\Gamma _{2}-\Gamma _{1}^{2}]^{2}}}}$

onde ${\displaystyle \Gamma _{i}=\Gamma (1+i/k)}$.

O excesso de curtose pode ser expresso por:

${\displaystyle \gamma _{2}={\frac {\lambda ^{4}\Gamma (1+{\frac {4}{k}})-4\gamma _{1}\sigma ^{3}\mu -6\mu ^{2}\sigma ^{2}-\mu ^{4}}{\sigma ^{4}}}-3}$

Função geradora de momentos

Uma variedade de expressões estão disponíveis para a função geradora de momentos de X. Como uma série de potências, dado que os momentos já são conhecidos, se tem

${\displaystyle E\left[e^{tX}\right]=\sum _{n=0}^{\infty }{\frac {t^{n}\lambda ^{n}}{n!}}\Gamma \left(1+{\frac {n}{k}}\right).}$

Alternativamente, pode-se tentar resolver diretamente a integral

${\displaystyle E\left[e^{tX}\right]=\int _{0}^{\infty }e^{tx}{\frac {k}{\lambda }}\left({\frac {x}{\lambda }}\right)^{k-1}e^{-(x/\lambda )^{k}}\,dx.}$

Para um parâmetro k pertencente aos números racionais, expresso como k = p/q onde p e q são inteiros, então essa integral pode ser resolvida analiticamente. Veja[4] para caso em que k é um inteiro, e [5] para o caso racional. Substituindo t por -t, se tem

${\displaystyle E\left[e^{-tX}\right]={\frac {1}{\lambda ^{k}\,t^{k}}}\,{\frac {p^{k}\,{\sqrt {q/p}}}{({\sqrt {2\pi }})^{q+p-2}}}\,G_{p,q}^{\,q,p}\!\left(\left.{\begin{matrix}{\frac {1-k}{p}},{\frac {2-k}{p}},\dots ,{\frac {p-k}{p}}\\{\frac {0}{q}},{\frac {1}{q}},\dots ,{\frac {q-1}{q}}\end{matrix}}\;\right|\,{\frac {p^{p}}{\left(q\,\lambda ^{k}\,t^{k}\right)^{q}}}\right)}$

onde G é a função Meijer G.

A função característica também pode ser obtida por [6].

Entropia de informação

A entropia da informação é dada por

${\displaystyle H(\lambda ,k)=\gamma \left(1\!-\!{\frac {1}{k}}\right)+\ln \left({\frac {\lambda }{k}}\right)+1}$

onde ${\displaystyle \gamma }$ é a constante de Euler-Mascheroni.

Estimação de parâmetros

Métodos gráficos

Métodos gráficos comumente aplicados apara o julgamento de qualidade de ajuste de dados a distribuição de Weibull são: papel de probabilidade de Weibull (descrito em detalhes na sessão abaixo), plots do tipo percentil-percentil e quantil-quantil. Métodos gráficos servem 2 propósitos:

• análise de dados no sentido de estimar parâmetros e validar um modelo
• apresentação dos dados métodos gráficos são de fácil entendimento e são ótimos para comunicar resultados.

Papel de probabilidade Weibull

O papel de probabilidade é uma técnica gráfica utilizada para verificar a adequação de um determinado modelo estatístico aos dados. Se uma amostragem segue a distribuição de Weibull, seu papel de probabilidade Weibull se distribuirá conforme uma reta numa espécie de gráfico quantil-quantil. O papel de probabilidade Weibull utiliza a função distribuição acumulada ${\displaystyle {\hat {F}}(x)}$ dos dados pois ela pode ser linearizada. Os eixos do papel de probabilidade Weibull são ${\displaystyle \ln(-\ln(1-{\hat {F}}(x)))}$ e ${\displaystyle \ln(x)}$.

${\displaystyle {\begin{aligned}F(x)&=1-e^{-(x/\lambda )^{k}}\\-\ln(1-F(x))&=(x/\lambda )^{k}\\\underbrace {\ln(-\ln(1-F(x)))} _{\textrm {'y'}}&=\underbrace {k\ln x} _{\textrm {'mx'}}-\underbrace {k\ln \lambda } _{\textrm {'c'}}\end{aligned}}}$

Um procedimento de regressão então é utilizado para a determinação dos parâmetros da reta m e c da reta y=mx+c a partir dos quais se determina os valores para o parâmetro de forma 'k' e de escala 'lambda' da distribuição ajustada. Existem diversas técnicas diferentes para a determinação e ordenação dos dados da função de distribuição acumulada ${\displaystyle {\hat {F}}(x)}$ e softwares de estatística oferecem algoritmos que facilitam o procedimento.

Papel de probabilidade de uma distribuição de Weibull

Métodos numéricos

Uma grande variedade de métodos numéricos são aplicados para análise de distribuição Weibull:

• Método dos mínimos quadrados
• Método dos momentos
• Máxima verossimilhança

Software

Além de softwares de uso comum para fins estatísticos como Minitab, SPSS, SAS, MATLAB, Excel, etc possuírem funções para análise de Weibull, existem diversos softwares especializados em análise de Weibull. Segue abaixo uma lista de softwares dedicados:

• Weibull ++ da Reliasoft Corp. [1]
• Relex Weibull pela Relex Software Corp. [2]
• WeibullPro pela Isograph Inc. [3]
• WinSMITH Weibull pela Barringer & Associates,Inc. [4]

Aplicações

O campo de aplicações da distribuição de Weibull é vasto e abrange praticamente todas as áreas da ciência. Usando essa distribuição, realizou-se a modelagem bem sucedida de dados provenientes de grandes áreas de ciências física, biológica, social, saúde e ambiental.

Engenharia de confiabilidade

Devido a necessidade de empresas da área de engenharia e tecnologia de assegurarem a confiabilidade e caracterizarem a vida útil de seus produtos originou-se o mercado da engenharia de confiabilidade no qual a análise de Weibull aparece como uma importante e poderosa ferramenta. Segue abaixo uma compilação de artigos com aplicações da distribuição de Weibull na área de confiabilidade de materiais e produtos:

• Resistência à fratura do vidro[1]
• Falha de compostos de fibra de carbono[7]
• Falha em semicondutores e capacitores[8]
• Confiabilidade de guias de ondas ópticos para cabos[9]
• Variabilidade de capacidade de carga de helicópteros[10]

Outras áreas

Compilação de artigos com aplicações da distribuição de Weibull em diversas áreas:

• Distribuição de velocidades do vento[11]
• Magnitude de terremotos[12]
• Análise da duração do desemprego[13]
• Dinâmica de biomassa da folhagem do pinheiro escocês[14]
• Incidência do câncer de pulmão em fumantes[15]

Relação com outras distribuições

• A distribuição de Weibull com 3 parâmetros tem uma densidade de probabilidade dada por

${\displaystyle f(x;k,\lambda ,\theta )={k \over \lambda }\left({x-\theta \over \lambda }\right)^{k-1}e^{-({x-\theta \over \lambda })^{k}}\,}$

para ${\displaystyle x\geq \theta }$ e f(x; k, λ, θ) = 0 parax < θ, onde ${\displaystyle k>0}$ é o parâmetro de forma, ${\displaystyle \lambda >0}$ é o parâmetro de escala e ${\displaystyle \theta }$ o parâmetro de localidade da distribuição. Quando θ=0, temos o caso da distribuição de Weibull com apenas 2 parâmetros apresentado na definição.

O parâmetro ${\displaystyle \theta }$ pertence aos reais e está definido de ${\displaystyle -\infty }$ a ${\displaystyle +\infty }$ e tem a mesma unidade que a variável x. Quando x tem unidade de tempo ${\displaystyle \theta }$ é denominado vida mínima. Em um contexto geral, ${\displaystyle \theta }$ é a origem da distribuição pois x está definido apenas para x>${\displaystyle \theta }$ (a equação atinge valores negativos se x<${\displaystyle \theta }$ saindo do escopo de definição de uma função densidade de probabilidade). Sendo assim, alterações no valor de ${\displaystyle \theta }$ resultam em uma translação da origem do gráfico da distribuição, no jargão estatístico ${\displaystyle \theta }$ é chamado de parâmetro de localidade. Em diversos contextos o tempo de origem não tem significado algum a não ser indicar o início do gráfico e por isso ${\displaystyle \theta }$ é igualado a 0 por conveniência e omitido, deixando a distribuição com apenas 2 parâmetros, k e ${\displaystyle \lambda }$.

• A distribuição de Weibull pode ser caracterizada como a distribuição de uma variável aleatória X tal que a variável aleatória

${\displaystyle Y=\left({\frac {X}{\lambda }}\right)^{k}}$

é a distribuição exponencial padrão com intensidade 1.[3]

Referências

1. W. Weibull: A statistical distribution function of wide applicability, J. Appl. Mech. 18, 293–296 (1951)
2. Papoulis, Pillai, "Probability, Random Variables, and Stochastic Processes, 4th Edition
3. Johnson, Kotz & Balakrishnan 1994
4. (Cheng, Tellambura & Beaulieu 2004)
5. (Sagias & Karagiannidis 2005)
6. Muraleedharan et al. (2007)
7. S. D. Durham, W. J. Padgett: Cumulative damage model for system failure with application to carbon fibers and composites, Technometrics 39, 34–44 (1997)
8. GOTTFRIED, P. / ROBERTS, H.R. (1963): Some pitfalls of the Weibull distribution; Proceedings of the 9th Nat. Symp. Rel. Qual. Cont., 372–379
9. LIERTZ, H. / OESTREICH, U.H.P. (1976): Application of Weibull distribution to mechanical reliability of optical waveguides for cables; Siemens Forschungs- und Entwicklungsber. 5, 129–135
10. BOORLA, R. / ROTENBERGER, K. (1997): Load variability of two–bladed helicopters; Journal of American Helicopters 42, 15–26
11. M. Al-Hasan, R. R. Nigmatullin: Identification of the generalized Weibull distribution in wind speed data by the Eigen-coordinates method, Renewable Energ. 28(1), 93–110 (2003)
12. T. Huillet, H. F. Raynaud: Rare events in a log- Weibull scenario—Application to earthquake magnitude data, Eur. Phys. J. B 12, 457–469 (1999)
13. K. Roed, T. Zhang: A note on the Weibull distribution and time aggregation bias, Appl. Econ. Lett. 9, 469–472 (2002)
14. R. A. Fleming: The Weibull model and an ecological application: describing the dynamics of foliage biomass on Scots pine, Ecol. Model. 138(1-3), 309–319 (2001)
15. WHITTENMORE, A. / ALTSCHULER, B. (1976): Lung cancer incidence in cigarette smokers: Further analysis of DOLL and HILL’s data for British physicians; Biometrica 32, 805–816

Ligações externas

• http://www.portalaction.com.br/1033-distribui%C3%A7%C3%A3o-de-weibull
• http://www.reuk.co.uk/Wind-Speed-Distribution-Weibull.htm
• http://www.mathpages.com/home/kmath122/kmath122.htm
• http://www.mathpages.com/home/kmath498/kmath498.htm