ja %E6%96%B9%E3%81%B9%E3%81%8D%E3%81%AE%E5%AE%9A%E7%90%86

方べきの定理（方冪の定理、方羃の定理、方巾の定理^[1]、ほうべきのていり、英: power of a point theorem^[2]）は、平面初等幾何学の定理の1つである。

定理の主張

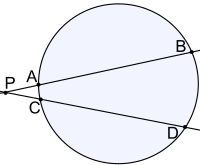
（図1、図2）円 O とその円周上にない点 P について、点 P を通る2本の直線 $\ell$ , m がともに円の割線（円との共有点が2個である直線）になっているとしよう。円と $\ell$ の交点を A, B とし、円と m の交点を C, D とすると、

{\text{PA}}\cdot {\text{PB}}={\text{PC}}\cdot {\text{PD}}

が成り立つ。

（図3）また、P が円 O の外側にあり、P を通る直線の一方が円 O の接線となる場合にも、円と割線の交点を A, B とし、円と接線の接点を T とすると、

{\text{PA}}\cdot {\text{PB}}={\text{PT}}^{2}

が成り立つ。

P が円 O の内側にある場合		左の図において、同一の弧に対する円周角は互いに等しいから ∠PAC = ∠PDB ∠PCA = ∠PBD 二角相等により △PAC ∽ △PDB よって PA: PC = PD: PB すなわち PA ・ PB = PC ・ PD
P が円 O の外側にある場合		左の図において、円に内接する四角形の外角の大きさは、その内対角の大きさに等しいから、 ∠PAC = ∠PDB ∠PCA = ∠PBD 二角相等により △PAC ∽ △PDB よって PA: PC = PD: PB すなわち PA ・ PB = PC ・ PD
直線の一方が接線になる場合		左の図において、接弦定理により、 ∠PTA = ∠PBT また、共通の角として ∠TPA = ∠BPT 二角相等により △PAT ∽ △PTB よって PA: PT = PT: PB すなわち PA ・ PB = PT²

方べきの定理は、適当な意味においてその逆が成立することが知られている。

平面上に相異なる4点 A, B, C, D があり、直線 AB と直線 CD がただ一つの交点 P をもつとする。ここで次の条件を考える。

(1)かつ(2-1)を満たすならば、4点 A, B, C, D を通る円（共円）が存在し、P はこの円の内側にある。

(1)かつ(2-2)を満たすならば、4点 A, B, C, D を通る円が存在し、P はこの円の外側にある。

また、平面上に相異なる3点 A, B, T があり、直線 AB 上に点 P があるとする。ここで次の条件を考える。

(3)かつ(4)かつ(5)を満たすならば、3点 A, B, T を通る円（△ABTの外接円）の T における接線は P を通る。

いずれの場合も、もとの定理の証明を逆向きにたどるようにして、三角形の相似を利用して証明することができる。条件(2-1), (2-2), (4), (5)を外すことができないことには注意すべきである。

この節では、円をその中心点の名前を借りて円 O のように呼ぶことはせず、独立した記号を与えることとする。

平面上に点 O, P と、O を中心とする円 ω がある。P を通る直線 $\ell$ が ω と1つまたは2つの共有点をもつとし、それを A, B とする（共有点が1つのときは A=B として扱う）。

さて、P と ω が動かずに、 $\ell$ がさまざまに動くとき、A, B はつられてさまざまに動くが、 ${\text{PA}}\cdot {\text{PB}}$ の値は変化しないことが方べきの定理からわかる。P≠O のとき、直線 OP を考えることにより、

{\text{PA}}\cdot {\text{PB}}=|{\text{PO}}-r|\cdot ({\text{PO}}+r)=|{\text{PO}}^{2}-r^{2}|

と表すことができる。P=O のときにも、ω の任意の直径を考えることにより、やはり

{\text{PA}}\cdot {\text{PB}}=r^{2}=|0-r^{2}|=|{\text{PO}}^{2}-r^{2}|

が成り立つ。

そこで、P と ω のみによって決まる量

\Pi _{\omega }(P)={\text{PO}}^{2}-r^{2}

を定義すると便利である。この値を、P の ω に関する方べきの値（ほうべきのあたい）または単に方べき（ほうべき、英: power）という。記号には $\Pi (P),{\text{Pow}}_{\omega }(P)$ などが用いられることもある。

方べきの値は、P が ω の外側にあれば正、ω の内側にあれば負、ちょうど ω の上にあればゼロとなる。

学校数学で方べきの値が教えられることは少ない。

平面上の異なる中心をもつ2つの円の根軸は、方べきの値を用いて特徴付けられる^[3]。

^ 「冪/羃」はひらがなで書かれることが多い。また、「巾」は数学者の間では「冪」の略字として用いられている。(詳しくは冪乗を参照されたい)
^ “Power of a Point Theorem”. 数学も英語も強くなる！意外な数学英語 Unexpected Math English. 2021年1月26日閲覧。
^ チェン 2023, pp. 42–44

H.S.M.コクセター著、銀林浩訳『幾何学入門』（上）、筑摩書房〈ちくま学芸文庫〉、2009年9月10日、161-165頁。ISBN 978-4-480-09241-0。
エヴァン・チェン『数学オリンピック幾何への挑戦ユークリッド幾何をめぐる船旅』森田康夫（監訳）、日本評論社、2023年2月15日、39-47頁。ISBN 978-4-535-78978-4。