太陽の断面構造 恒星の構造 (こうせいのこうぞう、英語 : Stellar structure )に関するモデルは恒星 の内部構造を詳細に記述し、光度 や色(スペクトル分類 )、恒星の進化 の予測を行う。星の階級や年齢によって元素 の構成やエネルギー輸送の機構が異なるために内部構造は異なっている。
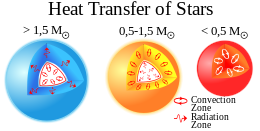
小質量星、中質量星、大質量星それぞれの熱輸送機構 恒星内部の熱は対流 や放射輸送 によって外部へ放出される。ただし、白色矮星 では熱伝導 によっても外部に熱が伝わる。恒星内のガス塊が断熱過程 によってわずかに上昇しただけでも上昇し続けるほど十分な温度勾配を持つ場合、対流はエネルギー輸送の主要なモードとなる。この場合、ガス塊が周囲の気体より高温であれば浮力が働いて上昇し続け、低温になれば元の高さまで下降していくこととなる[ 1] 不透明度 (英語版 )
主系列星 の内部構造はその星の重量によって異なる。
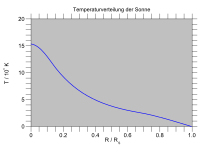
太陽 を含む0.3-1.5 M ☉ (太陽質量 )の恒星では、水素 からヘリウム への核融合 は主に陽子-陽子連鎖反応 を介して行われるため、急峻な温度勾配は形成されない。そのため、太陽質量前後の質量を持つ恒星の内層でのエネルギー輸送は、放射が支配的である。一方、外層では水素が中性水素原子となるほど低温となり、紫外線光子に対して不透明となるため、対流が支配的となる。このように、太陽質量前後の質量を持つ恒星では、内層に放射層が、外層に対流層が存在する構造となっている。
1.5 M ☉ より質量の大きな大質量星では、中心温度が1.8×107 K 以上となり、水素 がヘリウム に変換される核融合 の経路はCNOサイクル が主となる。エネルギー生成率はCNOサイクルで温度の15乗に比例するため、エネルギー生成率が温度の4乗に比例する陽子-陽子連鎖反応より大きなエネルギーが生み出される[ 2] 対流 が見られる。恒星の外層では、温度勾配はより緩やかであるものの、水素がほぼ完全にイオン化し、紫外線に対してもほぼ透明な状態を保つほど高温となる。このため、恒星の外側では主に放射が見られる。
質量が小さい主系列星では、放射層が存在せず、恒星全体において対流がエネルギー輸送の主要な要素となっている[ 3]
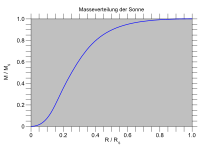
恒星モデル (英語版 ) 定常状態 かつ球対称であると仮定した球対称準静的モデルである。このモデルでは4つの一次微分方程式を定めることができ、うち2つは物質 や圧力 の半径に対する依存性を表す方程式で、もう2つは温度 や光度 の半径に対する依存性を表した方程式である[ 4]
仮定した球対称性を用いて恒星の構造方程式を立てる際には、恒星の中心から
r
{\displaystyle r}
d
r
{\displaystyle {\mbox{d}}r}
密度
ρ
(
r
)
{\displaystyle \rho (r)}
T
(
r
)
{\displaystyle T(r)}
P
(
r
)
{\displaystyle P(r)}
l
(
r
)
{\displaystyle l(r)}
ϵ
(
r
)
{\displaystyle \epsilon (r)}
熱力学的平衡 にあると考えているので、物質や光子 の温度は同一であると仮定している。しかし、厳密には任意の距離にある球殻の温度は常に方程式を解いて求まる温度よりも高くなるので局所的な熱力学的平衡は成立しない。だが、光子の平均自由行程
λ
{\displaystyle \lambda }
λ
≪
T
/
|
∇
T
|
{\displaystyle \lambda \ll T/|\nabla T|}
一つ目の微分方程式は、恒星内の静水圧平衡 を表した式である。この式は恒星中の圧力勾配 による外向きの力と内向きの重力 が釣り合っていることを表す。
d
P
d
r
=
−
G
m
ρ
r
2
{\displaystyle {{\mbox{d}}P \over {\mbox{d}}r}=-{Gm\rho \over r^{2}}}
ここで、
m
(
r
)
{\displaystyle m(r)}
r
{\displaystyle r}
G は重力定数 を表す。累積質量は、以下の連続の方程式 に伴って半径と共に増加する。
d
m
d
r
=
4
π
r
2
ρ
.
{\displaystyle {{\mbox{d}}m \over {\mbox{d}}r}=4\pi r^{2}\rho .}
質量連続の方程式を恒星の中心(
r
=
0
{\displaystyle r=0}
r
=
R
{\displaystyle r=R}
球殻から出るエネルギーを考慮すると、以下のエネルギー方程式が得られる
d
l
d
r
=
4
π
r
2
ρ
(
ϵ
−
ϵ
ν
)
{\displaystyle {{\mbox{d}}l \over {\mbox{d}}r}=4\pi r^{2}\rho (\epsilon -\epsilon _{\nu })}
ここで、
ϵ
ν
{\displaystyle \epsilon _{\nu }}
ニュートリノ から生じる光度である。(なお、このニュートリノは通常の物質との反応なしに恒星から脱出する。) 恒星の核外部では核反応は起こっておらずエネルギーが生じていないので、光度は一定となる。
エネルギー輸送方程式はエネルギー輸送の形態によって異なる形をとる。白色矮星 によく当てはまる熱伝導性のエネルギー輸送の場合、以下のようなエネルギー方程式が立てられる
d
T
d
r
=
−
1
k
l
4
π
r
2
,
{\displaystyle {{\mbox{d}}T \over {\mbox{d}}r}=-{1 \over k}{l \over 4\pi r^{2}},}
k は熱伝導率 である。
放射エネルギー輸送の場合、主系列星 の内、太陽質量程度の恒星の内側と大質量星の恒星の外側には以下のエネルギー方程式がよくあてはまる。
d
T
d
r
=
−
3
κ
ρ
l
64
π
r
2
σ
T
3
,
{\displaystyle {{\mbox{d}}T \over {\mbox{d}}r}=-{3\kappa \rho l \over 64\pi r^{2}\sigma T^{3}},}
κ
{\displaystyle \kappa }
不透明度 (英語版 )
σ
{\displaystyle \sigma }
シュテファン=ボルツマン定数 である。
対流エネルギー輸送では、厳密な数式による定式化がなされていないが気体の乱流 がエネルギー輸送に関わるとされている。対流エネルギー輸送は通常、混合長理論 (英語版 ) [ 5] 単原子 理想気体 の場合、対流が断熱的であるということは対流する気体分子が周囲の気体と熱交換を行わないこととなり、混合長は次のようになる
d
T
d
r
=
(
1
−
1
γ
)
T
P
d
P
d
r
,
{\displaystyle {{\mbox{d}}T \over {\mbox{d}}r}=\left(1-{1 \over \gamma }\right){T \over P}{{\mbox{d}}P \over {\mbox{d}}r},}
なお、
γ
=
c
p
/
c
v
{\displaystyle \gamma =c_{p}/c_{v}}
比熱 比である断熱指数 を表す。対流が断熱的でない場合、温度勾配はこの方程式と一致しない。例えば、太陽では対流層の底部は太陽の中心核付近となっており、中心核付近は断熱的であるが、対流層の表面付近は断熱的ではない。混合長理論ではモデルを観測値に合わせるために2つの任意のパラメータを含んでいる。つまり厳密的に定式化しているというよりは、現象論としての性質のある理論である[ 6]
また圧力、不透明度、エネルギー生成率を温度、密度、化学的組成など星内物質の特性に結び付ける状態方程式 が必要になる。不透明度は一つの公式では正確に表すことができず、特定の密度や温度で様々な組成のそれぞれで表計算される[ 7] 原子核物理学 の実験から計算される[ 6] [ 8]
以上の方程式の解は一連の境界条件との組み合わせにより、恒星の挙動を完全に記述する。典型的な境界条件により、恒星の表面部(
r
=
R
{\displaystyle r=R}
r
=
0
{\displaystyle r=0}
P
(
R
)
=
0
{\displaystyle P(R)=0}
m
(
0
)
=
0
{\displaystyle m(0)=0}
m
(
R
)
=
M
{\displaystyle m(R)=M}
有効温度 (
T
(
R
)
=
T
e
f
f
{\displaystyle T(R)=T_{eff}}
上記のような単純化されたモデルは、恒星の進化により組成の変化が十分早い場合に補正なしでは適当ではなくなる。静力学的平衡の方程式は、恒星半径の変化が非常に速い時、半径方向の加速度の項を修正する必要がある場合もあり得る[ 9] [ 10]
^ Hansen, Kawaler & Trimble (2004 , §5.1.1)^ Hansen, Kawaler & Trimble (2004 , Tbl. 1.1)^ Hansen, Kawaler & Trimble (2004 , §2.2.1)^ This discussion follows those of, e. g., Zeilik & Gregory (1998 , §16-1–16-2) and Hansen, Kawaler & Trimble (2004 , §7.1)
^ Hansen, Kawaler & Trimble (2004 , §5.1)^ a b Ostlie, Dale A. and Carrol, Bradley W., An introduction to Modern Stellar Astrophysics
^ Iglesias, C. A.; Rogers, F. J. (June 1996), “Updated Opal Opacities”, Astrophysical Journal 464 : 943–+, Bibcode : 1996ApJ...464..943I , doi :10.1086/177381 . ^ Rauscher, T.; Heger, A.; Hoffman, R. D.; Woosley, S. E. (September 2002), “Nucleosynthesis in Massive Stars with Improved Nuclear and Stellar Physics”, The Astrophysical Journal 576 (1): 323–348, arXiv :astro-ph/0112478 , Bibcode : 2002ApJ...576..323R , doi :10.1086/341728 . ^ Moya, A.; Garrido, R. (August 2008), “Granada oscillation code (GraCo)”, Astrophysics and Space Science 316 (1–4): 129–133, arXiv :0711.2590 , Bibcode : 2008Ap&SS.316..129M , doi :10.1007/s10509-007-9694-2 . ^ Mueller, E. (July 1986), “Nuclear-reaction networks and stellar evolution codes – The coupling of composition changes and energy release in explosive nuclear burning”, Astronomy and Astrophysics 162 : 103–108, Bibcode : 1986A&A...162..103M .
Kippenhahn, R.; Weigert, A. (1990), Stellar Structure and Evolution , Springer-Verlag Hansen, Carl J.; Kawaler, Steven D.; Trimble, Virginia (2004), Stellar Interiors (2nd ed.), Springer, ISBN 0-387-20089-4 Kennedy, Dallas C.; Bludman, Sidney A. (1997), “Variational Principles for Stellar Structure”, Astrophysical Journal 484 (1): 329, arXiv :astro-ph/9610099 , Bibcode : 1997ApJ...484..329K , doi :10.1086/304333 Weiss, Achim; Hillebrandt, Wolfgang; Thomas, Hans-Christoph; Ritter, H. (2004), Cox and Giuli's Principles of Stellar Structure , Cambridge Scientific Publishers Zeilik, Michael A.; Gregory, Stephan A. (1998), Introductory Astronomy & Astrophysics (4th ed.), Saunders College Publishing, ISBN 0-03-006228-4