ポリトロープ(英語: polytrope)とは、宇宙物理学、流体力学および熱力学で用いられる、流体の状態に関する関係式である。分野により若干の意味の相違がある。
宇宙物理学におけるポリトロープ
宇宙物理学や流体力学において、ポリトロープとは、圧力と密度がある関係式(ポリトロピックな関係という)を満たし、力学平衡にある球対称な流体である。ポリトロープ流体、ポリトロープ球、ポリトロープガス球などとも呼ばれる。ポリトロープの内部構造は静水圧平衡やレーン=エムデン方程式を用いて記述される。
一般に、圧力P と密度ρの間に、

の関係があるとき、この関係式をポリトロピックと呼ぶ。ここで、n はポリトロピック指数、K は比例定数である。この条件に従う気体は実際にレーン=エムデン方程式に対するポリトロピックな解として現れるが、この関係式は状態方程式と解釈される必要はない。むしろ、単純にρの変化に伴うP の変化についての仮定を表す関係式である。
ポリトロープ流体の状態方程式については、流体力学でよく知られる完全流体を用いれば一般的に十分である。
ポリトロピック指数による分類
ポリトロープは様々な天体を記述するモデルとして用いられる。ポリトロピック指数n が大きくなるにつれて、流体の中心密度は高くなる。
- n = ∞のポリトロープ…等温ガス球と呼ばれ、球状星団と同様の星同士が衝突する構造を持つ。
ポリトロープの密度分布
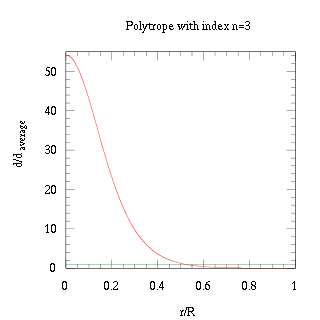
以下の図はポリトロープの密度分布である。横軸はポリトロープの半径を1としたときの中心からの距離、縦軸は平均密度を1としたときの密度を表す。
-
n = 1のポリトロープの密度分布。
-
n = 1.5のポリトロープの密度分布。
-
n = 3のポリトロープの密度分布。
熱力学におけるポリトロープ
熱力学においてポリトロープ過程[1]とは、気体の準静的過程の一種である。摩擦、放熱などの若干の損失をともなう装置における準断熱過程の近似として用いられる。ポリトロープ指数をn とし、以下の気体(ここでは理想気体とする)の圧力P 、密度ρ、温度T の間の関係式で表される:


ポリトロープ過程(1→2)の間に気体に加えられる熱量q は

で与えられる。ここでcvは定積比熱、κは比熱比である。この式から、

をポリトロープ比熱と呼ぶことがある。
以下のより基本的な過程はポリトロープ過程の特別の場合に帰着される:
脚注
- ^ 佐藤俊、国友孟『熱力学』丸善、1984年、32頁。ISBN 4-621-02917-7。
参考文献
- Chandrasekhar, S. [ 1939 ] ( 1958 ). An Introduction to the Study of Stellar Structure, New York : Dover. ISBN 0-486-60413-6
- Hansen, C.J., Kawaler S.D. & Trimble V. ( 2004 ). Stellar Interiors - Physical Principles, Structure, and Evolution, New York : Springer. ISBN 0-387-20089-4
- Horedt, G.P. ( 2004 ). Polytropes. Applications in Astrophysics and Related Fields, Dordrecht : Kluwer. ISBN 1-4020-2350-2
関連項目