ja %E4%B8%89%E8%A7%92%E5%BD%A2%E3%81%AE%E5%86%85%E6%8E%A5%E5%86%86%E3%81%A8%E5%82%8D%E6%8E%A5%E5%86%86

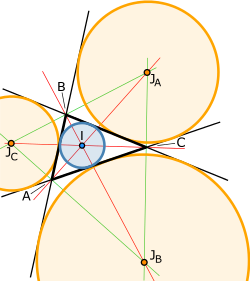初等幾何学において三角形の内接円（ないせつえん、英: incircle / inscribed circle (of a triangle)）とは、その三角形の内部にあり3辺に接する円である。三角形の内部にある円の中で最も面積が大きい円である。内接円の中心を内心（ないしん、incenter）と呼ぶ。

傍接円（ぼうせつえん、excircle）は、三角形の外側にあり1辺と他の2辺の延長線に接する円である。傍接円の中心を傍心（ぼうしん、excenter）と呼ぶ。全ての三角形は、各辺に接する合計3つの傍接円を持つ。

内心は、3つの角の二等分線上にある。傍心は、1つの角の二等分線と他の2つの角の外角の二等分線上にある。内心と傍心は「三角形の3つの頂点と垂心」という位置関係にある。

三角形の面積との関係

内接円と傍接円の半径は、三角形の面積に関係している。

$S$ を三角形の面積、 $a, b, c$ を3辺の長さ、 $s$ を半周長 ( $= (a + b + c)/2$ ) としたとき、ヘロンの公式から、

{\begin{aligned}S&={\frac {1}{4}}{\sqrt {(a+b+c)(a-b+c)(b-c+a)(c-a+b)}}\\&={\sqrt {s(s-a)(s-b)(s-c)}}\end{aligned}}

一方、内接円の半径 $r$ は、

r={\frac {2S}{a+b+c}}={\sqrt {\frac {(s-a)(s-b)(s-c)}{s}}}

頂点A に対する傍接円の半径 $r A$ は、

r_{\text{A}}={\frac {2S}{-a+b+c}}={\sqrt {\frac {s(s-b)(s-c)}{s-a}}}

となる。（他の2頂点B,Cに関する傍接円の半径も同様である）

これらの式から、三角形の面積は、内接円の半径と、各辺に対する傍接円の半径との積の平方根に等しいことが容易に導かれる。

→「リュイリエの定理 § 派生項目」も参照

また、傍接円は内接円より大きいことと最も長い辺に対応する傍接円が最も大きいことが分かる。

内接円に関連する点

九点円とフォイエルバッハ点

内接円と傍接円は、九点円と接する。この接点をフォイエルバッハ点という。

ジェルゴンヌ点とジェルゴンヌ三角形

頂点を A, B, C とし、内接円が各辺と接する点を T_A, T_B, T_C とする（T_A は A の対辺上にあるとする）。⊿T_AT_BT_C をジェルゴンヌ三角形という。接触三角形(contact triangle,intouch triangle)とも呼ばれる^[1]。元の三角形の内接円はこの三角形の外接円になる。3直線 AT_A, BT_B, CT_C は1点で交わる。この点をジェルゴンヌ点という。

AT_A, BT_B, CT_C が1点で交わることから、⊿ABC が不等辺三角形のとき「AB と T_AT_B の交点」「CA と T_CT_A の交点」「BC と T_BT_C の交点」は同一直線上にある。この線をジェルゴンヌ線という。⊿ABC が二等辺三角形のときは上記の辺の組のうち1つが平行になるが、残りの2点を結ぶことで直線が定義できる。⊿ABC が正三角形の場合はこの直線は定義できない。

内心の座標

座標平面における内心の座標は、3頂点の重み付き平均の値として求めることができる。

3頂点の座標を (x_a,y_a), (x_b,y_b), (x_c,y_c)、3辺の長さを a, b, c としたとき、

{\bigg (}{\frac {ax_{a}+bx_{b}+cx_{c}}{a+b+c}},{\frac {ay_{a}+by_{b}+cy_{c}}{a+b+c}}{\bigg )}={\frac {a}{a+b+c}}(x_{a},y_{a})+{\frac {b}{a+b+c}}(x_{b},y_{b})+{\frac {c}{a+b+c}}(x_{c},y_{c})

.

となる。

三線座標で表すと 1 : 1 : 1
- 絶対三線座標では r : r : r
重心座標で表すと a : b : c

となる。

円の式

x : y : z を三線座標で表したときの点の座標は、u = cos²A/2, v = cos²B/2, w = cos²C/2 とすると、円上の点に対して以下の式が成り立つ。

内接円：u²x² + v²y² + w²z² - 2vwyz - 2wuzx - 2uvxy = 0
- A に対する傍接円：u²x² + v²y² + w²z² - 2vwyz + 2wuzx + 2uvxy = 0
- B に対する傍接円：u²x² + v²y² + w²z² + 2vwyz - 2wuzx + 2uvxy = 0
- C に対する傍接円：u²x² + v²y² + w²z² + 2vwyz + 2wuzx - 2uvxy = 0

その他の関係

内心と傍心の中点は全て外接円上にある（トリリウムの定理）。さらに、傍心同士の中点も全て外接円上にある（九点円の性質の系）。
3つの傍接円の半径の逆数の和は、内接円の半径の逆数に等しい（リュイリエの定理）。
- 四面体と内接・傍接球、あるいはさらに高次の単体と内接・傍接球に対しても同様の関係が成り立つ。
三角形の内接円の半径は、『三種類の「頂点から内接円との接点までの距離」の辺を持つ直方体』と同じ体積の『同じ三角形を面に持つ柱』の高さと等しくなる。
内心と外心との距離は、ナーゲル点と垂心との距離の半分である。

脚注

^ Weisstein, Eric W.. “Contact Triangle” (英語). mathworld.wolfram.com. 2024年4月6日閲覧。

外部リンク

『傍心の意味と性質・内心との比較』 - 高校数学の美しい物語
proof of triangle incenter - PlanetMath.（英語）
Definition:Incircle of Triangle at ProofWiki
Definition:Excircle of Triangle at ProofWiki

[1] Weisstein, Eric W.. “Contact Triangle” (英語). mathworld.wolfram.com. 2024年4月6日閲覧。

[1]

三角形の内接円と傍接円