|
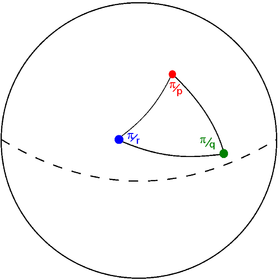
Triangolo di SchwarzIn geometria, un triangolo di Schwarz è un triangolo sferico che può essere utilizzato per tassellare una sfera (creando una cosiddetta tassellatura sferica), eventualmente sovrapponendosi, attraverso continue riflessioni sui suoi bordi. Tali triangoli sono stati classificati dal matematico tedesco Hermann Schwarz nel 1873 e sono stati così chiamati proprio in suo onore. I triangoli di Schwarz possono essere più generalmente definiti come una tassellatura della sfera, del piano euclideo o di un piano iperbolico, tuttavia, ogni triangolo di Schwarz su una sfera definisce un gruppo finito, mentre su un piano euclideo o iperbolico essi definiscono un gruppo infinito. Un triangolo di Schwarz è rappresentato da tre numeri razionali (p q r) ciascuno dei quali rappresenta uno dei suoi angoli al vertice, essendo in particolare il quoziente dell'angolo piatto diviso per il valore dell'angolo al vertice. Ciò implica ad esempio che se uno dei tre numeri è un 2, il triangolo in questione sarà un triangolo rettangolo . Quando tutti e tre i numeri sono interi, il triangolo è chiamato triangolo di Möbius e corrisponde a una tassellatura non sovrapposta, inoltre il gruppo di simmetria è chiamato gruppo triangolare. Su una sfera è possibile individuare tre triangoli di Möbius più una famiglia a un solo parametro; nel piano euclideo ci sono tre triangoli di Möbius, mentre nello spazio iperbolico c'è una sola famiglia di triangoli di Möbius a tre parametri.[1] Soluzione spazialeIl dominio fondamentale a forma di triangolo (p q r), con angoli al vertice π/p, π/q, e π/r, può esistere in spazi diversi a seconda del valore della somma dei reciproci di questi interi: Questo è semplicemente un modo per dire che nello spazio euclideo la somma degli angoli interni di un triangolo è pari a π, mentre su una sfera è pari a un angolo maggiore di π e nello spazio iperbolico è pari a un angolo minore di π. Rappresentaziona graficaUn triangolo di Schwarz può essere rappresentato graficamente come un grafo triangolare. In esso, ogni nodo rappresenta un lato del triangolo di Schwarz, ed è etichettato con il corrispondente ordine di riflessione, dato da π/angolo al vertice.
Immaginando i bordi del triangolo come specchi su cui avvengono delle riflessioni, i bordi di ordine 2 rappresentano specchi perpendicolari che possono essere ignorati in questo diagramma, anche per questo, la rappresentazione di tale grafo triangolare con un diagramma di Coxeter-Dynkin non mostra bordi di ordine 2. Per una notazione più semplice si può utilizzare un gruppo di Coxeter, in tal modo da (p q 2) si ha [p,q] per triangoli rettangoli, mentre per (p 2 2) si ha [p]×[]. Lista dei triangoli di SchwarzTriangoli di Möbius per la sfera
I triangoli di Möbius, che come detto sono triangoli di Schwarz con parametri interi, includono una famiglia con un parametro libero e tre casi eccezionali:
Triangoli di Schwarz per la sfera elencati per densitàI triangoli di Schwarz (p q r), raggruppati per densità:[2][3]
Triangoli per il piano euclideo
Densità 1:
Densità 2:
Densità ∞:
Triangoli per il piano iperbolico
Densità 1:
Densità 2:
Densità 3:
Densità 4:
Densità 6:
Densità 10:
Il triangolo di Schwarz (2 3 7) è il più piccolo dei triangoli di Schwarz iperbolici, e risulta essere di particolare interesse. Il suo gruppo triangolare (o più precisamente il gruppo di von Dyck di indice 2 di isometrie che preservano l'orientazione) è il gruppo triangolare (2,3,7), che è poi il gruppo universale dei gruppi di Hurwitz. Tutti i gruppi di Hurwitz sono quozienti del gruppo triangolare (2,3,7) e tutte le superfici di Hurwitz sono tassellabili con il triangolo di Schwarz (2 3 7). Il più piccolo gruppo Hurwitz è il gruppo semplice di ordine 168, il secondo più piccolo è il gruppo semplice non abeliano, che è isomorfo al gruppo speciale lineare proiettivo PSL(2,7), e la superficie di Hurwitz associata (di genere 3) è la quartica di Kleinc. Il triangolo (2 3 8) tassella la superficie di Bolza, una superficie di genere 2 altamente simmetrica ma non appartenente alle superfici di Hurwitz. Note
Collegamenti esterni
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Portal di Ensiklopedia Dunia
![{\displaystyle {\begin{aligned}{\frac {1}{p}}+{\frac {1}{q}}+{\frac {1}{r}}&>1{\text{ : Sfera}}\\[8pt]{\frac {1}{p}}+{\frac {1}{q}}+{\frac {1}{r}}&=1{\text{ : Piano euclideo}}\\[8pt]{\frac {1}{p}}+{\frac {1}{q}}+{\frac {1}{r}}&<1{\text{ : Piano iperbolico}}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f684235fb1d5d11a63cc7446eb953d0340dda271)