Trasformata di Fourier veloce
|
Read other articles:

Concert hall in Downtown Atlanta, Georgia, United States For other uses, see Tabernacle (disambiguation). The TabernacleExterior of the venue (c.2009)Former namesHouse of Blues (1996-97)Address152 Luckie St NWAtlanta, GA 30303-2006LocationDowntown AtlantaOwnerLive NationCapacity2,600ConstructionBroke groundAugust 17, 1909 (1909-08-17)OpenedSeptember 3, 1911 (1911-09-03)Renovated1994-9620082014Construction cost$125,000($4.09 million in 2023 dollars[1])Ar…

ПосёлокБайкальский Прибой 51°56′16″ с. ш. 106°11′54″ в. д.HGЯO Страна Россия Субъект Федерации Бурятия Муниципальный район Кабанский Сельское поселение «Большереченское» Внутреннее деление 5 улиц История и география Часовой пояс UTC+8:00 Население Население ↘118[1&#…
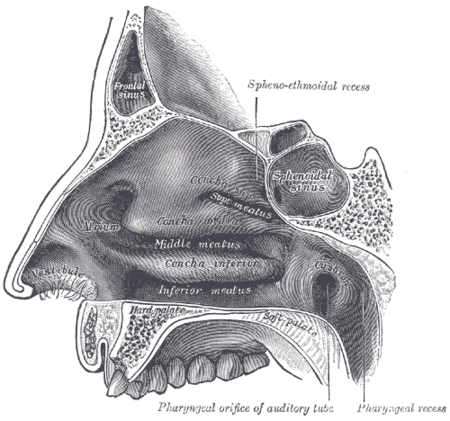
Disambiguazione – Se stai cercando il significato relativo all'araldica, vedi Palato (araldica). Questa voce o sezione sull'argomento anatomia è priva o carente di note e riferimenti bibliografici puntuali. Sebbene vi siano una bibliografia e/o dei collegamenti esterni, manca la contestualizzazione delle fonti con note a piè di pagina o altri riferimenti precisi che indichino puntualmente la provenienza delle informazioni. Puoi migliorare questa voce citando le fonti più precisamente. …

American swimmer Brooke BennettPersonal informationFull nameBrooke Marie BennettNational team United StatesBorn (1980-05-06) May 6, 1980 (age 44)Tampa, FloridaHeight5 ft 5 in (1.65 m)Weight126 lb (57 kg)SportSportSwimmingStrokesFreestyleClubBrandon Blue Wave Medal record Women's swimming Representing the United States Olympic Games 1996 Atlanta 800 m freestyle 2000 Sydney 400 m freestyle 2000 Sydney 800 m freestyle World Championships (LC) 1998 Perth …

Canal crossing central Scotland The Forth and Clyde Canal, near Bonnybridge and Larbert The Forth and Clyde Canal is a canal opened in 1790, crossing central Scotland; it provided a route for the seagoing vessels of the day between the Firth of Forth and the Firth of Clyde at the narrowest part of the Scottish Lowlands. This allowed navigation from Edinburgh on the east coast to the port of Glasgow on the west coast. The canal is 35 miles (56 km) long and it runs from the River Carron at Gr…

Северный морской котик Самец Научная классификация Домен:ЭукариотыЦарство:ЖивотныеПодцарство:ЭуметазоиБез ранга:Двусторонне-симметричныеБез ранга:ВторичноротыеТип:ХордовыеПодтип:ПозвоночныеИнфратип:ЧелюстноротыеНадкласс:ЧетвероногиеКлада:АмниотыКлада:Синапсиды…

Vous lisez un « article de qualité » labellisé en 2007. Richesse des nations Édition de Londres (1776) de la Richesse des nations Auteur Adam Smith Pays Royaume-Uni Genre Économie Éditeur W. Strahan and t. Cadell, Londres Date de parution 1776 modifier Recherches sur la nature et les causes de la richesse des nations (en anglais, An Inquiry into the Nature and Causes of the Wealth of Nations), ou plus simplement la Richesse des nations, est le plus célèbre ouvrage d…

Carthage (la) Archidioecesis Carthaginensis Informations générales Type de juridiction Siège titulaire Église Église catholique Création v. 50 Église La cathédrale Saint-Louis de Carthage est devenue un musée Direction actuelle Pape François Province ecclésiastique Province ecclésiastique de Carthage (d) Plus haute juridiction Saint-Siège Localisation Siège Carthage Pays Tunisie (en) Notice sur www.catholic-hierarchy.org modifier Vestiges de la basilique dite de Saint-Cyprien…

English actor Dex LeeLee in 2023Born (1993-05-16) 16 May 1993 (age 30)Edmonton, EnglandEducationThe Latymer SchoolMorgan Aslanoff School of DanceArtsEdOccupationActorYears active2014–presentTelevisionDoctorsRelativesMiriam-Teak Lee (sister) Dex Lee (born 16 May 1993) is an English actor, known for his role as Bear Sylvester on the BBC soap opera Doctors. Before he was cast in Doctors, he appeared in numerous professional stage productions and worked part-time as a dance teacher. Earl…

English composer and organist(1711–1779) William Boyce by John Russell, 1776 William Boyce (baptised 11 September 1711 – 7 February 1779) was an English composer and organist. Like Beethoven later on, he became deaf but continued to compose. He knew Handel, Arne, Gluck, Bach, Abel, and a very young Mozart, all of whom respected his work. Life William Boyce by Thomas Hudson, ca. 1745 Boyce was born in London, at Joiners Hall, then in Lower Thames Street, to John Boyce, at the time a joiner an…

American composer (1937–2023) David Del TrediciBorn(1937-03-16)March 16, 1937Cloverdale, California, U.S.DiedNovember 18, 2023(2023-11-18) (aged 86)New York City, U.S.Alma materUniversity of California, BerkeleyPrinceton UniversityOccupationComposerKnown forNeo-RomanticismNotable workIn Memory of a Summer DayTattooAwardsPulitzer Prize for Music (1980)Guggenheim FellowWoodrow Wilson Fellowship David Walter Del Tredici (March 16, 1937 – November 18, 2023) was an American compose…

Bosnian singer This biography of a living person needs additional citations for verification. Please help by adding reliable sources. Contentious material about living persons that is unsourced or poorly sourced must be removed immediately from the article and its talk page, especially if potentially libelous.Find sources: Dražen Žerić – news · newspapers · books · scholar · JSTOR (April 2021) (Learn how and when to remove this message) Dražen Žerić…

Highest court in the U.S. state of Michigan Michigan Supreme CourtEstablished1836LocationLansing, Michigan, United StatesComposition methodSemipartisan electionAuthorized byMichigan ConstitutionAppeals toSupreme Court of the United StatesJudge term length8 yearsNumber of positions7 (including chief justice)WebsiteOfficial WebsiteChief JusticeCurrentlyElizabeth T. ClementSinceNovember 22, 2022 The Michigan Supreme Court is the highest court in the U.S. state of Michigan. It is Michigan's court of…

1986 Connecticut Attorney General election ← 1982 November 4, 1986 1990 → Nominee Joe Lieberman Richard E. Arnold Party Democratic Republican Popular vote 613,742 335,209 Percentage 64.7% 35.3% County resultsLieberman: 50–60% 60–70% 70–80% Attorney General before election Joe Lieberman Democratic Elected Attorney General Joe Lieberman Democratic Elections in Connectic…

Conquista romana della Gallia Cisalpinaparte delle guerre romano-celticheLa provincia romana della Gallia CisalpinaDataIII–II secolo a.C. LuogoGallia cisalpina Casus belliEspansionismo romano EsitoVittoria romana e annessione della pianura padana SchieramentiRepubblica romanaTribù galliche, Tribù liguri, Reti Voci di guerre presenti su Wikipedia Manuale Con l'espressione conquista della Gallia Cisalpina si indica la campagna di sottomissione dei popoli delle regioni che oggi formano l'attual…

Río Ocklawaha El río desde el puente de Ferry en StarkesUbicación geográficaCuenca Río St. JohnsNacimiento Lago GriffinDesembocadura Río St. JohnsCoordenadas 29°28′13″N 81°41′25″O / 29.4702, -81.6904Ubicación administrativaPaís Estados UnidosEstado FloridaCondados Lake, Putnam y MarionCuerpo de aguaLongitud 119 kmSuperficie de cuenca n/d km²Caudal medio n/d m³/sAltitud Nacimiento: n/d mDesembocadura: n/d mMapa de localización Cuenca y curso del r�…

أطلانطسمعلومات عامةجزء من ميثولوجيا إغريقية موجود بالقرب من المسطح المائي المحيط الأطلسي[1] موجود في عمل The Time Stealer (en) [2]عشرون ألف فرسخ تحت الماءالماسة الزرقاء تعديل - تعديل مصدري - تعديل ويكي بيانات خارطة أثناسيوس كيرشر عن جزيرة اطلنطس في وسط المحيط الأطلسي. من موندو�…

Defunct American department store Barneys New York Inc.Former store, downtown San FranciscoCompany typePrivateIndustryRetailFounded1923; 101 years ago (1923) in New York City, New York, United StatesFounderBarney PressmanDefunctFebruary 22, 2020; 4 years ago (2020-02-22) (US stores)FateChapter 11 bankruptcy and liquidation, intellectual property acquired by Authentic Brands GroupHeadquartersNew York City, New York, United StatesNumber of locations 22 (at peak,…

Attacchi missilistici su Gəncəparte della seconda guerra del Nagorno KarabakhData4 ottobre 2020, 8 ottobre 2020, 10 ottobre 2020, 17 ottobre 2020 LuogoGəncə TipoAttacco missilistico Forze in campoEseguito daHaykakan banak (forze armate armene) BilancioPerdite civili26 morti, 125 feriti voci di bombardamenti aerei presenti su Wikipedia Gli attacchi missilistici su Gəncə del 2020 (in azero: Gəncə bombalanmaları) comprendono quattro diversi attacchi missilistici compiuti contro la città d…

1992 American TV series or program O Pioneers!VHS coverGenreDramaBased onO Pioneers!by Willa CatherTeleplay byRobert W. LenskiDirected byGlenn JordanStarring Jessica Lange David Strathairn Tom Aldredge Music byBruce BroughtonCountry of originUnited StatesOriginal languageEnglishProductionExecutive producerCraig AndersonProducerGlenn JordanCinematographyDick BushEditorScott ConradRunning time99 minutesProduction companies Prairie Films Craig Anderson Productions Lorimar Television Hallmark Hall o…















