|
Superficie minimaIn geometria differenziale, si definisce superficie minima (o, meno usato, superficie minimale, dall'inglese minimal surface) una superficie che ha curvatura media uguale a zero in ogni punto. La teoria delle superfici minime è strettamente correlata ai problemi di area minima: date una o più curve chiuse nello spazio, trovare, tra tutte le superfici aventi le curve date come bordo, quella che ha area minima. La superficie soluzione del problema, oltre a minimizzare l'area, avrà anche curvatura media nulla ovunque, quindi sarà una superficie minima. Non vale il viceversa, cioè non tutte le superfici minime aventi delle date curve chiuse nello spazio come bordo sono superfici che minimizzano l'area per il bordo assegnato. I problemi matematici che traggono spunto da situazioni osservabili nella vita quotidiana sono tra i più antichi nella storia della matematica. Alcune fonti riportano che fu Archimede ad introdurre in geometria i concetti di lunghezza e area minima. Egli capì che la linea più corta che congiunge due punti nello spazio è la linea retta, e che data una qualunque curva chiusa piana, la superficie di area minima avente come bordo la curva data è proprio la parte di piano delimitata dalla curva stessa. I problemi di area minima nei casi in cui siano date più curve chiuse nello spazio, oppure una sola curva non piana, sono più difficili da risolvere rispetto al caso particolare trattato da Archimede e rappresentano dei tipici problemi di quel ramo della matematica denominato calcolo delle variazioni. Una rappresentazione fisica di una superficie minima si può ottenere attraverso l'utilizzo di acqua e sapone: immergendo nell'acqua saponata un telaietto di ferro di una qualunque forma chiusa, all'estrazione del telaio, la lamina di sapone che rimane attaccata ad esso rappresenta una superficie "minima". In questo caso le virgolette sono d'obbligo, in quanto, ad esempio, se il telaio ha la forma di una circonferenza e viene estratto mantenendo il piano della circonferenza parallelo al suolo, la superficie di sapone verrà minimamente piegata verso il basso a causa della gravità, non quindi producendo una superficie minima (controesempi di tale natura si posso ricreare con qualsiasi altra forma). Un siffatto esperimento risulterebbe valido solo se eseguito in assenza di un campo gravitazionale, ciò permetterebbe la formazione di superficie con curvatura media nulla in ogni punto.[1] Evoluzione storica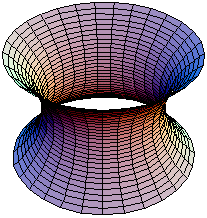 Il primo ad affrontare il problema della superficie di area minima fu Eulero nel 1744. Nel suo lavoro di calcolo delle variazioni Methodus inveniendi lineas curvas maximi minimive proprietate gaudentes egli affronta il problema di trovare la superficie di area minima che ha come bordo due circonferenze nello spazio poste su piani paralleli ed allineate in modo che il segmento che congiunge i centri delle due circonferenze risulti perpendicolare ad entrambi i piani su cui giacciono le due circonferenze. Vista la particolare geometria del problema, Eulero cerca la superficie soluzione del problema tra le superfici di rotazione, in particolare egli reimposta il problema in maniera tale da cercare la funzione il cui grafico, fatto ruotare in modo da descrivere le due circonferenze assegnate, generi la superficie cercata. Eulero dimostra che la curva cercata deve essere un arco di catenaria. La superficie ottenuta dalla rotazione della catenaria è detta catenoide. È proprio da questo tipo di problemi di area minima che nasce la teoria delle superfici minime. Data di nascita ufficiale è il 1762, anno di pubblicazione della memoria di Lagrange Essai d'une nouvelle méthode pour déterminer les maxima et les minima des formules intégrales indéfinies. In questa, Lagrange determina l'equazione differenziale che deve essere necessariamente soddisfatta da tutti i punti della superficie che minimizza l'area per un qualunque contorno nello spazio. L'equazione trovata è chiamata equazione di Eulero-Lagrange e, proprio con riferimento al problema dell'area minima, Lagrange chiama superficie minima ogni superficie che soddisfa l'equazione di Eulero-Lagrange, per questo detta anche equazione delle superfici minime. Nel 1776 Meusnier si accorge del significato geometrico dell'equazione di Eulero-Lagrange: se in un punto una superficie soddisfa l'equazione di Eulero-Lagrange, allora in quel punto la curvatura media della superficie è uguale a zero. Quindi le superfici minime sono quelle superfici che hanno la curvatura media uguale a zero ovunque, e le superfici che risolvono il problema dell'area minima sono superfici minime. Inoltre Meusnier scopre, tra le superfici rigate, una nuova superficie minima: l'elicoide retto. Per lungo tempo il piano, la catenoide e l'elicoide retto restano le uniche superfici minime note. Superfici minime e grafici di funzioni Un altro importante tassello della teoria delle superfici minime viene posto da Monge nel 1783 che, nell'opera Sur une méthode d'intégrer les équations aux différences ordinaires scopre un'importante relazione tra superfici minime e superfici di area minima: data una curva chiusa dello spazio che non si autointerseca (cioè una curva chiusa semplice), se una superficie che ha come bordo la curva data è anche il grafico di una funzione differenziabile, allora per questa superficie l'essere superficie minima è condizione necessaria e anche sufficiente a garantire che la sua area è minore dell'area di qualunque altra superficie avente la curva data come bordo. Cioè, nel caso di superfici che sono grafici di funzioni differenziabili, vale quello che non vale in generale: l'essere superficie minima basta a garantire l'essere una superficie che risolve il problema dell'area minima per una qualche curva chiusa e semplice dello spazio. Negli anni che vanno dal 1831 al 1835 Scherk scopre nuovi esempi di superfici minime. Tra queste, due famose superfici che noi oggi conosciamo con il nome di superficie di Scherk e seconda superficie di Scherk. Il problema di PlateauIl problema di Plateau è un classico problema di instabilità fluidodinamica. Intorno alla metà del diciannovesimo secolo il fisico belga Plateau inizia lo studio delle forme assunte dalle lamine saponate. Plateau sfrutta le proprietà fisiche dell'acqua saponata e le forze di tensione superficiale per costruire numerosi modelli geometrici di superfici minime.  La più semplice superficie minima che possiamo ottenere dall'acqua saponata è il piano, che si ottiene immergendo un filo di ferro chiuso in modo da formare una circonferenza. Una delle prime forme che Plateau ottiene è quella della catenoide che si ottiene immergendo nell'acqua saponata un telaio formato da due anelli metallici posti in modo da essere paralleli e abbastanza vicini, l'equivalente cioè del problema di Eulero della superficie di area minima il cui bordo è costituito dalle circonferenze dei due anelli. La pellicola che si viene a creare all'estrazione del telaio dall'acqua saponata ha la forma di una catenoide a causa del bilancio delle forze idrodinamiche a conferma (sperimentalmente) della validità della soluzione trovata da Eulero. La spiegazione fisica è da ricercare nel fatto che, essendo la pressione interna uguale a quella esterna, in ogni punto deve essere, per l'equilibrio idrodinamico, che la forza di tensione superficiale esterna bilanci quella interna (sia uguale e opposta); siccome la tensione superficiale è proporzionale alla curvatura della superficie il risultato è pertanto una superficie che ha curvatura media uguale a zero in ogni punto. Plateau si rende anche conto di un fatto abbastanza interessante che riguarda le catenoidi: date le due circonferenze del problema di Eulero, quando i piani su cui queste giacciono sono abbastanza vicini le catenoidi che passano dalle due circonferenza sono due, una più incurvata dell'altra. Entrambe le catenoidi sono superfici minime, ma ovviamente solo una delle due risolve il problema dell'area minima. Questo caso fornisce un esempio di superficie minima che non è la superficie di area minima per un bordo assegnato. Delle due catenoidi passanti dalle circonferenze date, quella più incurvata ha area maggiore e non può mai essere ottenuta come lamina saponata. Le superfici minime delle quali è possibile trovare un modello con le lamine di sapone vengono chiamate stabili. L'elicoide retto è una superficie minima stabile. Plateau riesce ad ottenerlo usando un telaietto di filo di ferro modellato ad elica. Durante i suoi esperimenti, Plateau riesce sempre ad ottenere una lamina saponata, qualunque sia la forma del telaio usato. Questi esperimenti quindi dimostravano, sperimentalmente, che le superfici minime finora conosciute non erano che una piccolissima parte delle superfici minime esistenti, delle quali bisognava però trovare le espressioni matematiche. Visto il successo degli esperimenti di Plateau, da allora il problema di trovare la superficie di area minima avente come bordo un qualunque numero di curve chiuse nello spazio prende il nome di problema di Plateau. "Prima età dell'oro" della teoria delle superfici minimeNegli anni che vanno dal 1850 al 1880 la ricerca si incentra sul problema di Plateau e si cercano le soluzioni soprattutto per contorni che hanno la forma di quadrilateri nello spazio. Nel 1865 Schwarz trova la soluzione nel caso in cui il contorno è costituito da quattro spigoli di un tetraedro. Inoltre egli individua alcune regole di simmetria che governano la forma delle superfici minime. Queste regole sono oggi note con il nome di principio di riflessione di Schwarz, grazie al quale Schwarz riesce a costruire nuove superfici minime illimitate e periodiche. Oltre a Schwarz altri matematici, tra cui Bernhard Riemann e Karl Weierstrass, risolvono il problema di Plateau per svariati contorni poligonali. Nuovi esempi di superfici minimeIl piano, la catenoide e l'elicoide retto sono superfici minime regolari (cioè lisce, prive di punte o spigoli), illimitate e prive di autointersezioni. Le superfici minime di questo tipo vengono dette illimitate immerse (dove il termine immerse indica proprio la mancanza di autointersezioni). Inoltre, il piano e la catenoide hanno anche curvatura totale finita. Fino al 1984 non si conoscevano altre superfici minime illimitate immerse con curvatura totale finita oltre al piano e alla catenoide. Per lungo tempo i matematici si sono chiesti se esistessero altre superfici minime di questo tipo, e una serie di risultati di non esistenza, ottenuti negli anni precedenti al 1984 e che dimostravano come non potessero esistere superfici del genere in molti casi particolari, faceva supporre che ciò non fosse possibile. Nel novembre del 1983 il matematico americano David Hoffman viene a conoscenza di una nuova superficie minima presentata nella tesi di dottorato di uno studente brasiliano, Celso Costa. Costa aveva dimostrato che quella da lui trovata era una superficie minima illimitata di curvatura totale finita, ma le equazioni che la definivano erano talmente complicate che nessuno sapeva che forma potesse avere e se fosse o meno una superficie immersa. Con l'aiuto di William Meeks III e l'uso di un programma di grafica computerizzata sviluppato da James Hoffman, Hoffman riuscì a dimostrare che la superficie di Costa era priva di autointersezioni. Qualche mese dopo, Hoffman e Meeks dimostrarono l'esistenza di una intera famiglia di superfici minime immerse. Nessuna di queste superfici, compresa la superficie di Costa, è ottenibile con le lamine di sapone. Dalla matematica ad altri campiEsempi di superfici minime possono incontrarsi in campi diversi dalla matematica:
Note
Bibliografia
Voci correlateAltri progetti
Collegamenti esterni
|
Portal di Ensiklopedia Dunia