|
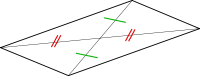
Symétrie (transformation géométrique)Une symétrie géométrique est une transformation géométrique involutive[1] qui conserve le parallélisme[2]. Parmi les symétries courantes, on peut citer la réflexion (ou symétrie orthogonale) et la symétrie centrale. Une symétrie géométrique est un cas particulier de symétrie. Il existe plusieurs sortes de symétries dans le plan ou dans l’espace. Remarque : Le terme de symétrie possède aussi un autre sens en mathématiques. Dans l'expression groupe de symétrie, une symétrie désigne une isométrie quelconque. Ce terme désigne soit une translation, soit un automorphisme orthogonal, soit la composée des deux. Symétrie dans le planSymétrie centrale (par rapport à un point)PrésentationLa symétrie de centre O est la transformation qui, à tout point M, associe le point M' tel que O soit le milieu de [MM']. Construction : Tracez la droite (d) passant par A et O. Prolongez la au-delà de O. Avec un compas pointé en O et un écartement égal à OA, recoupez (d) en A'. Le seul point invariant de cette symétrie est le point O. Une symétrie de centre O est aussi une rotation d’angle plat et une homothétie de centre O et de rapport -1 Centre de symétrieUne figure possède un centre de symétrie C si elle est invariante par la symétrie de centre C.  Exemples de centre de symétrie :
Groupe des symétries centrales-translationsLa composée de deux symétries de centres O et O', sO' o sO est une translation de vecteur  Cette propriété permet de définir un premier groupe de transformations du plan : celui des symétries centrales-translations. En effet, en composant deux symétries centrales ou translations, on obtient une symétrie centrale ou une translation. Et, pour obtenir l’application identique, il suffit de composer une translation de vecteur u par la translation de vecteur -u, ou de composer une symétrie centrale par elle-même. La symétrie centrale conserve les distances et les angles orientés. C’est donc une isométrie positive ou déplacement. Le groupe défini précédemment est donc un sous-groupe du groupe des déplacements. Symétrie axiale ou orthogonale par rapport à une droitePrésentationOn les appelle aussi des réflexions d’axe (d). La réflexion d’axe (d) est la transformation du plan qui laisse tous les points de (d) invariants et qui, à tout point M non situé sur (d), associe le point M' tel que (d) soit la médiatrice de [MM']. Comme il existe deux définitions équivalentes de la médiatrice, on connaît ainsi deux constructions équivalentes du point M'. ConstructionDonnées : l'axe de symétrie (d), le point A'. Objectif : construire A' symétrique de A par la symétrie orthogonale d'axe (d).
Axe de symétrieUne figure possède un axe de symétrie (d) si et seulement si elle est invariante par la réflexion d’axe (d) Exemples de figures usuelles :
Une figure possédant deux axes de symétrie perpendiculaires a pour centre de symétrie le point d’intersection des deux droites. Par exemple, les lettres H, I, O, X dans des polices de caractère simples (non cursives et non italiques) possèdent souvent deux axes de symétrie perpendiculaires, donc aussi un centre de symétrie, de même le rectangle, le losange et le carré. Réflexion et groupe des isométriesLa réflexion conserve les distances et les angles. C’est donc une isométrie. Mais elle ne conserve pas l’orientation (voir chiralité). On dit que c’est un antidéplacement.
On remarque alors que l’ensemble des réflexions génère tout l’ensemble des isométries. Symétrie obliqueLa symétrie par rapport à une droite (d) suivant une direction (d') (non parallèle à (d)) est la transformation qui laisse tous les points de (d) invariants et qui, à tout point M non situé sur (d) associe le point M' tel que la droite (MM') soit parallèle à (d') et le milieu de [MM'] soit sur (d) Cette symétrie est bien involutive : le symétrique de M’ est bien M. Elle offre moins d’intérêt que ses cousines car elle ne conserve pas les distances: elle déforme les figures. Cependant, elle conserve les barycentres et fait donc partie des transformations affines. Symétrie dans l’espaceSymétrie centrale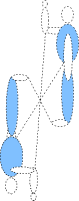 On retrouve la même définition et les mêmes propriétés que pour la symétrie centrale dans le plan, à ceci près qu’une symétrie centrale ne conserve pas l’orientation dans l’espace. Le bonhomme lève la main droite et son image lève la main gauche. Symétrie orthogonale par rapport à une droite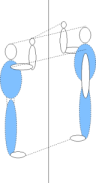 On retrouve la même définition que dans le plan. Une symétrie orthogonale par rapport à une droite est aussi une rotation d’axe (d) et d’angle plat. Contrairement à ce qui se passe dans le plan, une telle symétrie dans l’espace conserve l’orientation. Le bonhomme lève la main droite et son image lève la main droite. Symétrie orthogonale par rapport à un plan La symétrie orthogonale par rapport au plan (P) est la transformation qui laisse tous les points de (P) invariants et qui, à tout point M non situé sur (P), associe le point M’ tel que (P) soit le plan médiateur de [MM'] Une telle symétrie conserve les distances et les angles, mais ne conserve pas l'orientation. Par exemple, quand vous levez la main droite devant votre miroir, votre image lève sa main gauche. On démontre que l'ensemble des symétries par rapport à des plans génère par composition tout l'ensemble des isométries de l'espace. Les symétries obliquesOn peut tout aussi bien définir des symétries d’axe (d) selon la direction (P) ou des symétries par rapport à (P) suivant la direction (d), à condition que tout sous-espace égal ou parallèle à (P) ne contienne pas entièrement (d) ni ne soit entièrement contenu dans (d) et que leur intersection se réduise à un seul point (sinon ces transformations ne sont pas des symétries mais des projections). Mais ces transformations ne sont pas des isométries si (d) et (P) ne sont pas orthogonaux. Ces transformations (de même que les projections) conservent cependant les barycentres et sont des cas particuliers de transformations affines de l’espace. Notes et références
Voir aussi |
Portal di Ensiklopedia Dunia