|
Parcours de Graham En informatique, et en géométrie algorithmique, le parcours de Graham (aussi appelé algorithme de Graham[2]) est un algorithme pour le calcul de l'enveloppe convexe d'un ensemble de points dans le plan. Son principal intérêt est sa complexité algorithmique en O(n log n) où n est le nombre de points. Cet algorithme doit son nom à Ronald Graham, qui a publié l'algorithme original en 1972[3]. Enveloppe convexe Un ensemble est convexe si, lorsque l'on prend deux points dans l'ensemble, le segment qui joint ces deux points est entièrement inclus dans l'ensemble. L'enveloppe convexe d'un ensemble est le plus petit ensemble (pour l'inclusion) convexe qui contient les points. L'ensemble convexe d'un ensemble fini de points est un polygone. Le problème du calcul de l'enveloppe convexe est défini comme suit :
Les sommets de l'enveloppe sont parmi les n points données en entrée. On suppose dans la suite que l'on souhaite que les sommets données en sortie sont dans le sens trigonométrique (anti-horaire, autrement dit dans le sens contraire des aiguilles d'une montre). AlgorithmeL'algorithme prend en entrée un tableau de n points, comme montré sur la figure suivante :  Calcul d'un point pivotLa première étape de cet algorithme consiste à rechercher le point de plus petite ordonnée, appelé pivot. Si plusieurs points ont la même plus petite ordonnée, l'algorithme choisit parmi eux le point de plus petite abscisse. Comme montré dans la figure suivante, le pivot est le point le plus en bas à gauche. On échange le pivot avec le point numéro 1, de sorte que le pivot devienne maintenant le point numéro 1. 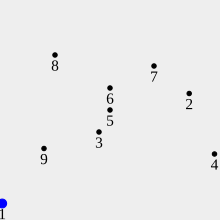 Tri des pointsL'ensemble des points est ensuite trié en fonction de l'angle que chacun d'entre eux fait avec l'axe des abscisses relativement au pivot ; le pivot garde sa première position dans le tableau. N'importe quel algorithme de tri par comparaison convient pour cela, par exemple le tri par tas ou le tri fusion (qui sont optimaux et ont une complexité de O(n log n)). À l'issue de cette étape, on dispose d'un tableau T contenant les points ainsi triés. La figure suivante montre les points qui ont été renumérotés afin de respecter l'ordre du tri.  On remarque qu'il n'y a pas besoin de calculer effectivement l'angle réel entre l'axe des abscisses et une droite (1i) pour un point i = 2..n. On peut par exemple calculer la pente de la droite (1i), ou alors se limiter à la comparaison des tangentes, ou bien même utiliser le produit en croix des coordonnées pour connaître les positions relatives des points. ItérationsL'algorithme construit itérativement l'enveloppe convexe (en vert sur la figure suivante). On débute avec le pivot. Puis on examine les points dans l'ordre du tableau trié (le point à examiner est représenté en noir). À chaque étape, on regarde s'il y a un « tournant à gauche » (comme dans les étapes 2, 5, 13, 15 sur l'exemple donné dans la figure) ou un « tournant à droite » (comme dans les étapes 10, 17, 18 de l'exemple).
À la fin (étape 19 puis 20), l'algorithme a calculé l'enveloppe convexe.  Déterminer si trois points constituent un « tournant à gauche » ou un « tournant à droite » ne requiert pas de calculer l'angle réel entre les deux segments, et peut être réalisé par simple arithmétique. Pour trois points (x1, y1), (x2, y2) et (x3, y3), il suffit de calculer le sens du produit vectoriel des deux vecteurs définis par les points (x1, y1), (x2, y2) et (x1, y1), (x3, y3), donné par le signe de l'expression (x2 – x1)(y3 – y1) – (y2 – y1)(x3 – x1). Si le résultat est nul, les points sont alignés. S'il est positif, les trois points constituent un « tournant à gauche ». Dans le cas contraire, c'est un « tournant à droite ». Ce processus retournera finalement au point auquel il a commencé, auquel cas l'algorithme sera terminé, et retourne les points formant l'enveloppe convexe, dans l'ordre inverse des aiguilles d'une montre : sur l'exemple, les points numéro 1, 2, 3, 6 et 9. Pseudo-codeSoit T un ensemble de points à examiner, représenté sous la forme d'un tableau indexé à partir de un. Au cours de l'algorithme, le polygone en cours de construction est stocké dans une pile. fonction parcours_de_Graham(T[1,.., n])
trouver le pivot et le placer en T[1];
trier le tableau T[2..n] par angle croissant par rapport au pivot (les points d'angle égal seront triés par abscisse croissante)
pile.empiler(T[1]);
pile.empiler(T[2]);
pour i = 3 à n
tant que (pile.hauteur >= 2) et (T[i] à droite du segment [pile.second, pile.sommet])
pile.dépiler;
pile.empiler(T[i]);
retourner pile
où pile.sommet désigne le point qui est sur le sommet de la pile et pile.second désigne le point sous le sommet de la pile. Pour tester qu'un point A est à gauche d'un segment [BC], on vérifie que le produit vectoriel est négatif, c'est-à-dire on vérifie que produitVectoriel(A, B, C) ≤ 0 où produitVectoriel est défini par : fonction produit_vectoriel(A, B, C)
retourner (B.x - A.x) * (C.y - A.y) - (C.x - A.x) * (B.y - A.y);
Note : pour gérer les cas dégénérés où l'enveloppe convexe a moins de trois points, un seul point devrait être entré dans la pile au départ, et si jamais la pile a moins de deux points (elle en aura au moins toujours un), alors le sommet de la pile devrait être également sorti si le nouveau point est le point considéré. En d'autres termes, la condition du « tant que » devrait être comme suit. pile.hauteur >= 2 et produit_vectoriel(pile.second, pile.sommet, T[i]) <= 0
ou pile.sommet == T[i]
Complexité algorithmiqueLa complexité en temps pour trouver du pivot est en O(n), n étant le nombre de points de l'ensemble. Le tri des points peut se faire avec une complexité en temps en O(n log n). La complexité de la boucle principale peut sembler être O(n2), parce que l'algorithme revient en arrière à chaque point pour évaluer si l'un des points précédents est un « tournant à droite ». En effet, les boucles pour i = 3 à n et tant que sont imbriquées. Mais, en fait la boucle est bien en O(n). En effet, chaque point est empilé au plus une fois. Ainsi, tous les calculs réalisés dans la boucle "tant que" est au plus en O(n). La complexité globale de l'algorithme est donc en O(n log n), puisque la complexité du tri domine la complexité du calcul effectif de l'enveloppe convexe. DiscussionsComparaison avec d'autres algorithmesAu lieu de trier selon l'angle, on peut trier selon les abscisses, puis on construit l'enveloppe convexe en deux étapes : la partie supérieure puis la partie inférieure. Cette modification a été créé par A. M. Andrew[4] et s'appelle le Andrew's Monotone Chain Algorithm. Ce nouvel algorithme a les mêmes propriétés que l'algorithme de Graham[5]. L'utilisation d'une pile dans l'algorithme de Graham est similaire à celle faite dans l'algorithme pour le problème all nearest smaller values. D'ailleurs, il y a des algorithmes parallèles pour ce problème qui peuvent être utilisés pour calculer l'enveloppe convexe plus efficacement[6]. Robustesse numériqueLa robustesse numérique concerne le comportement d'un algorithme par rapport à la précision des nombres flottants. Un article de 2004 étudie comment et pourquoi l'algorithme de Graham peut mal se comporter à cause d'une mauvaise précision[7]. L'article[8] propose une solution. Une extension de l'algorithme Graham, appelée algorithme Graham-Fortune[9] est plus stable. Notes et références(en) Cet article est partiellement ou en totalité issu de l’article de Wikipédia en anglais intitulé « Graham scan » (voir la liste des auteurs).
Voir aussiArticles connexesLiens externes
|