Liste de projections cartographiques

Cette liste recense différentes méthodes de projection cartographique.

Tableau de projections

Projection	Traduction graphique	Type	Propriétés	Inventeur	Année	Notes
Équirectangulaire = équidistante cylindrique = rectangulaire = parallélogrammatique		Cylindrique	Équidistante Aphylactique	Marin de Tyr	120	Les distances sont conservées le long des méridiens. Plate carrée : cas particulier ayant l'équateur comme parallèle de référence.
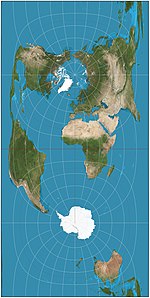
Cassini =Cassini Soldner		Cylindrique	Équidistante	César-François Cassini de Thury	1745	C'est la projection transverse à la projection équirectangulaire; Les distances le long du méridien central sont conservées. Les distances perpendiculaires au méridien central sont conservées.
Mercator = Wright		Cylindrique tangente	Conforme	Gerardus Mercator	1569	Conservation des angles mais pas des distances. Les zones polaires ne sont pas représentables.
Transverse Universelle de Mercator = UTM = Gauss-Krüger = Gauss conforme = Transverse Mercator ellipsoïdale		Cylindrique	Conforme	Carl Friedrich Gauss Johann Heinrich Louis Krüger	1822
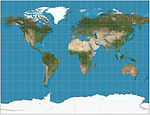
Stéréographique de Gall Similaire à Braun		Cylindrique	Compromis	James Gall	1885
Cylindrique de Miller = Miller		Cylindrique	Compromis	Osborn Maitland Miller	1942	Version proche de celle de Mercator permettant de couvrir les zones polaires.
Équivalente cylindrique de Lambert		Cylindrique	Équivalente	Johann Heinrich Lambert	1772
Behrmann		Cylindrique	Équivalente	Walter Behrmann	1910
Hobo-Dyer		Cylindrique	Équivalente	Mick Dyer	2002
Gall–Peters = Gall orthographic = Peters		Cylindrique	Équivalente	James Gall (Arno Peters)	1855
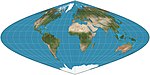
Sinusoïdale = Sanson-Flamsteed = Équivalente Mercator		Pseudo-cylindrique	Équivalente	(Plusieurs, la première est inconnue)	1600 (env.)
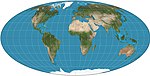
Mollweide = elliptique = Babinet = homolographique		Pseudo-cylindrique	Équivalente	Karl Brandan Mollweide	1805
Eckert II		Pseudo-cylindrique	Équivalente	Max Eckert-Greifendorff	1906
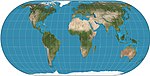
Eckert IV		Pseudo-cylindrique	Équivalente	Max Eckert-Greifendorff	1906
Eckert VI		Pseudo-cylindrique	Équivalente	Max Eckert-Greifendorff	1906
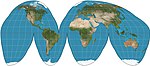
Goode		Pseudo-cylindrique	Équivalente	John Paul Goode	1923
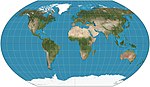
Kavrayskiy VII		Pseudo-cylindrique	Compromis	Vladimir V. Kavrayskiy	1939
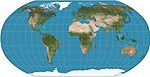
Robinson		Pseudo-cylindrique	Compromis	Arthur H. Robinson	1963
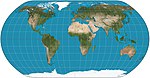
Natural Earth		Pseudo-cylindrique	Compromis	Tom Patterson	2011
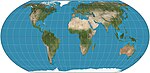
Equal Earth		Pseudo-cylindrique	Équivalente	Bojan Šavrič, Bernhard Jenny et Tom Patterson	2018
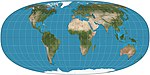
Hyperelliptique de Tobler		Pseudo-cylindrique	Équivalente	Waldo Tobler	1973
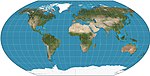
Wagner VI		Pseudo-cylindrique	Compromis	K.H. Wagner	1932
Collignon		Pseudo-cylindrique	Équivalente	Édouard Collignon	1865 (env.)
HEALPix		Pseudo-cylindrique	Équivalente	Krzysztof M. Górski	1997
Parabolique de Craster =Reinhold Putniņš P4		Pseudo-cylindrique	Équivalente	John Craster	1929
Projection quartique plane polaire = McBryde-Thomas n^o 4		Pseudo-cylindrique	Équivalente	Felix W. McBryde, Paul Thomas	1949
Authalique quartique		Pseudo-cylindrique	Équivalente	Karl Siemon Oscar Adams	1937 1944
The Times		Pseudo-cylindrique	Compromis	John Muir	1965
Loximutale		Pseudo-cylindrique		Karl Siemon, Waldo Tobler	1935, 1966
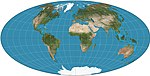
Aïtoff		Pseudo-azimutale	Compromis	David A. Aïtoff	1889
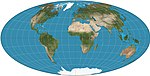
Hammer = Hammer-Aïtov variations : Briesemeister ; Nordique		Pseudo-azimutale	Équivalente	Ernst Hammer	1892
Winkel-Tripel		Pseudo-azimutale	Compromis	Oswald Winkel	1921
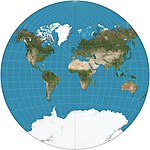
Van der Grinten		Autre	Compromis	Alphons J. van der Grinten	1904
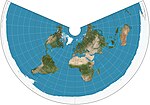
Conique équidistante = conique simple		Conique	Équidistante	Basée sur la 1^re projection de Ptolémée	100 (env.)
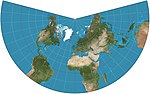
Conique conforme de Lambert		Conique	Conforme	Johann Heinrich Lambert	1772
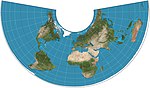
Conique d'Albers		Conique	Équivalente	Heinrich C. Albers	1805
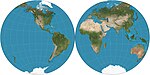
Globulaire de Nicolosi		Polyconique[1]		Abū Rayḥān al-Bīrūnī; réinventée par Giovan Battista Nicolosi, 1660[2] .:14	1000 (env.)
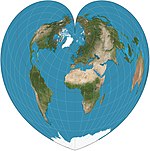
Werner		Pseudo-conique	Équivalente	Johannes Stabius	1500 (env.)
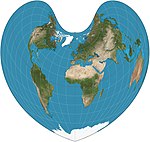
Bonne		Pseudo-conique, cordiforme	Équivalente	Bernardus Sylvanus	1511
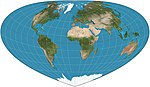
Bottomley		Pseudo-conique	Équivalente	Henry Bottomley	2003
Polyconique		Pseudo-conique		Ferdinand Rudolph Hassler	1820 (env.)
Postel =Azimutale équidistante zénithale équidistante		Azimutale	Équidistante	Al-Biruni	1000 (env.)
Gnomonique		Azimutale	Gnomonique	Thales (probablement)	580 av. J-C (env.)
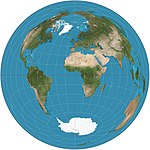
Azimutale équivalente de Lambert		Azimutale	Équivalente	Johann Heinrich Lambert	1772
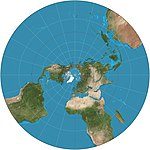
Stéréographique		Azimutale	Conforme	Hipparque	200 av J.-C. (env.)
Orthographique		Azimutale		Hipparque	200 av. J.-C. (env.)
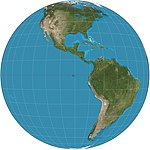
Perspective verticale		Azimutale		Matthias Seutter	1740
Équidistante deux-points		Azimutale	Équidistante	Hans Maurer	1919
Quinconce de Peirce		Autre	Conforme	Charles Sanders Peirce	1879
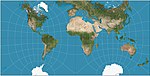
Guyou		Autre	Conforme	Émile Guyou	1887
Adams		Autre	Conforme	Oscar Sherman Adams	1925
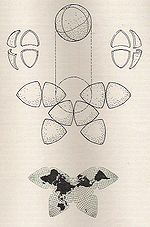
Cahill		Polyhédrale	Compromis	Bernard Joseph Stanislaus Cahill	1909
Cahill-Keynes		Polyhédrale	Compromis	Gene Keyes	1975
Papillon de Waterman		Polyhédrale	Compromis	Steve Waterman	1996
Cube sphérique quatrilatéralisé		Polyhédrale	Équivalente	F. Kenneth Chan, E. M. O’Neill	1973
Fuller		Polyhédrale	Compromis	Buckminster Fuller	1943
Projection myriadréale		Polyhédrale		Jarke J. van Wijk	2008
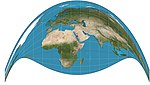
Rétro-azimutale de Craig = Mecca		Rétroazimutale		James Ireland Craig	1909
Hammer retroazimuthal, front hemisphere		Rétroazimutale		Ernst Hammer	1910
Rétro-azimutale de Hammer		Rétroazimutale		Ernst Hammer	1910
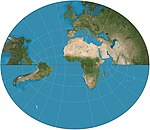
Littrow		Rétroazimutale		Joseph Johann Littrow	1833
Projection Authagraph		Tétrahédrale	quasi équivalente	Hajime Narukawa	1999	La carte est fabriquée par division égale d'une surface sphérique en 96 triangles transposés sur tétraèdre
Projection en octant		Polyhédrale	Compromis	Leonardo da Vinci	1514
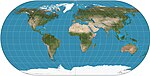
Ovale d'Ortelius		Pseudo-cylindrique	Compromis	Battista Agnese	1540
Cylindrique centrale		Cylindrique	Perspective	(inconnu)	1850 (env.)

Références

• (en) Cet article est partiellement ou en totalité issu de l’article de Wikipédia en anglais intitulé « List of map projections » (voir la liste des auteurs).

1. "Nicolosi Globular projection"
2. Snyder, John P., Flattening the earth: two thousand years of map projections, University of Chicago Press, 1993 (ISBN 0-226-76746-9)

Voir aussi

Articles connexes

• Projection cartographique
• Géodésie
• Carte inversée
• Géométrie projective

Liens externes