|
Inversion géométriqueEn géométrie, l'inversion géométrique est l'étude de l'inversion, une transformation du plan euclidien qui envoie des cercles ou des lignes vers d'autres cercles ou lignes et qui préserve les angles entre les courbes de croisement. De nombreux problèmes difficiles en géométrie voient leur résolution simplifiée lorsqu'une inversion est appliquée. L'inversion semble avoir été découverte par un certain nombre de personnes à la même époque, dont Steiner (1824), Quetelet (1825), Bellavitis (1836), Stubbs et Ingram (1842-3) et Kelvin (1845)[1]. Le concept d'inversion peut être généralisé aux espaces de dimension supérieure. Inversion dans un cercle Inverse d'un point Inverser un nombre en arithmétique signifie généralement prendre son inverse. Une idée étroitement liée en géométrie est celle de "l'inversion" d'un point. Dans le plan, l'inverse d'un point P par rapport à un cercle de référence (Ø) de centre O et de rayon r est un point P', situé sur le rayon O passant par P tel que C'est ce qu'on appelle l'inversion par un cercle ou l'inversion par un plan. L'inversion prenant tout point P (différent de O) à son image P' ramène également P' à P, donc le résultat de l'application de la même inversion deux fois est la transformation d'identité sur tous les points du plan autres que O (involution) . Pour faire de l'inversion une involution il faut introduire un point à l'infini, un seul point placé sur toutes les droites, et prolonger l'inversion, par définition, pour intervertir le centre O et ce point à l'infini. Il découle de la définition que l'inversion de tout point à l'intérieur du cercle de référence doit se trouver à l'extérieur de celui-ci, et vice versa, avec le centre et le point à l'infini changeant de position, tandis que tout point du cercle n'est pas affecté (est invariant par inversion). En résumé, plus un point est proche du centre, plus sa transformation est éloignée, et vice versa. Construction au compas et à la règle
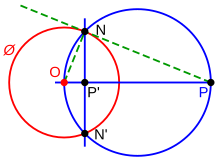 Pour construire l'inverse P' d'un point P extérieur à un cercle Ø :
Pour construire l'inverse P d'un point P' à l'intérieur d'un cercle Ø :
Construction de DuttaIl existe une construction du point inverse de A par rapport à un cercle P qui est indépendante du fait que A soit à l'intérieur ou à l'extérieur de P[2] . On considère un cercle P de centre O et un point A qui peut être à l'intérieur ou à l'extérieur du cercle P.
Propriétés
L'inversion d'un ensemble de points du plan par rapport à un cercle est l'ensemble des inverses de ces points. Les propriétés suivantes rendent l'inversion de cercle utile.
Les propriétés supplémentaires incluent :
Exemples en deux dimensions
ApplicationPour un cercle ne passant pas par le centre d'inversion, le centre du cercle en cours d'inversion et le centre de son image en inversion sont colinéaires au centre du cercle de référence. Ce fait peut être utilisé pour prouver que la droite d'Euler du triangle de contact d'un triangle coïncide avec sa ligne OI. La preuve va à peu près comme suit : On inverse par rapport au cercle inscrit du triangle ABC. Le triangle médian du triangle de contact est inversé en triangle ABC, c'est-à-dire que le centre circonscrit du triangle médial, c'est-à-dire que le centre du cercle d'Euler du triangle de contact, le centre et le centre circonscrit du triangle ABC sont colinéaires. Deux cercles non sécants peuvent être inversés en cercles concentriques. Ensuite, la distance d'inversion (généralement notée δ) est définie comme le logarithme népérien du rapport des rayons des deux cercles concentriques. De plus, deux cercles non sécants peuvent être inversés en cercles congruents, en utilisant un cercle d'inversion centré en un point sur le cercle d'antisimilitude. Le dispositif de Peaucellier-Lipkin est une implémentation mécanique de l'inversion dans un cercle. Il fournit une solution exacte au problème important de la conversion entre le mouvement linéaire et le mouvement circulaire. Pôle et polaire Si le point R est l'inverse du point P alors les droites perpendiculaires à la droite PR passant par l'un des points est la polaire de l'autre point (le pôle). Les pôles et les polaires ont plusieurs propriétés utiles :
En trois dimensions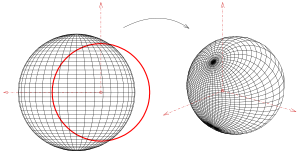   L'inversion par rapport à un cercle est généralisable à l'inversion par rapport à une sphère en trois dimensions. L'inversion d'un point P en 3D par rapport à une sphère de référence centrée en un point O de rayon R est un point P ' sur le rayon de direction OP tel que . Comme avec la version 2D, une sphère s'inverse en sphère, sauf que si une sphère passe par le centre O de la sphère de référence, alors elle s'inverse en un plan. Tout plan passant par O, s'inverse en une sphère touchant O. Un cercle, c'est-à-dire l'intersection d'une sphère avec un plan sécant, s'inverse en cercle, sauf si le cercle passe par O, auquel cas il s'inverse en droite. Cela se réduit au cas 2D lorsque le plan sécant passe par O, mais est un vrai phénomène 3D si le plan sécant ne passe pas par O. Exemples en trois dimensionsSphèreLa surface la plus simple (après le plan) est la sphère. La première image montre une inversion non triviale (le centre de la sphère n'est pas le centre d'inversion) d'une sphère avec deux faisceaux de cercles qui se croisent orthogonalement. Cylindre, cône, toreL'inversion d'un cylindre, d'un cône ou d'un tore donne un cyclide de Dupin (en). SphéroïdeUn sphéroïde est une surface de révolution et contient un faisceau de cercles qui est projeté sur un faisceau de cercles (voir image). L'image inverse d'un sphéroïde est une surface de degré 4. Hyperboloïde d'une feuilleUn hyperboloïde à une nappe, qui est une surface de révolution contenant un faisceau de cercles qui est projeté sur un faisceau de cercles. Un hyperboloïde à une nappe contient deux faisceaux de lignes supplémentaires, qui sont projetés sur des faisceaux de cercles. L'image montre une telle ligne (bleue) et son inversion. Projection stéréographique comme inversion d'une sphère Une projection stéréographique projette généralement une sphère à partir d'un point (pôle nord) de la sphère sur le plan tangent au point opposé (pôle Sud). Cette cartographie peut être réalisée par une inversion de la sphère sur son plan tangent. Si la sphère (à projeter) a pour équation (écrit alternativement ; de centre , de rayon , en vert sur l'image), alors il sera projeté par l'inversion par rapport à la sphère unité (rouge) sur le plan tangent au point . Les droites passant par le centre d'inversion (point ) sont projetés sur eux-mêmes. Ce sont les lignes de projection de la projection stéréographique. Coordonnées à 6 sphèresLes coordonnées à 6 sphères sont un système de coordonnées pour l'espace tridimensionnel obtenu en inversant les coordonnées cartésiennes. Axiomatique et généralisationL'un des premiers à considérer les fondements de la géométrie inversive fut Mario Pieri en 1911 et 1912[3]. Edward Kasner a rédigé sa thèse sur "La théorie des invariants du groupe d'inversion"[4]. Plus récemment, la structure mathématique de la géométrie inversive a été interprétée comme une structure d'incidence où les cercles généralisés sont appelés "blocs": En géométrie d'incidence, tout plan affine avec un seul point à l'infini forme un plan de Möbius, également appelé plan inversif. Le point à l'infini est ajouté à toutes les droites. Ces plans de Möbius peuvent être décrits axiomatiquement et existent à la fois dans des versions finies et infinies. Un modèle du plan de Möbius issu du plan euclidien est la sphère de Riemann. InvariantLe birapport entre 4 points est invariant par inversion. En particulier si O est le centre de l'inversion et et sont les distances aux extrémités d'une ligne L, puis la longueur de la ligne va devenir sous une inversion de centre O. L'invariant est : Relation avec le programme d'ErlangenSelon Coxeter[5], la transformation d'inversion par rapport à un cercle a été inventée par L.I. Magnus en 1831. Depuis lors, cette projection a ouvert la voie vers les mathématiques supérieures. À travers quelques étapes d'application de la projection d'inversion de cercle, un étudiant en géométrie des transformations apprécie rapidement l'importance du programme d'Erlangen de Felix Klein, une excroissance de certains modèles de géométrie hyperbolique. DilatationLa combinaison de deux inversions en cercles concentriques se traduit par une similitude, une homothétie ou une dilatation caractérisée par le rapport des rayons des cercles. RéciprocitéLorsqu'un point du plan est interprété comme un nombre complexe avec complexe conjugué alors l'inverse de z est Par conséquent, la forme algébrique de l'inversion dans un cercle unité est donnée par où:
La réciprocité est la clé de la théorie de la transformation en tant que générateur du groupe de Möbius. Les autres générateurs sont la translation et la rotation, tous deux familiers par des manipulations physiques dans l'espace 3 ambiant. L'introduction de la réciprocité (dépendante de l'inversion du cercle) est ce qui produit la nature particulière de la géométrie de Möbius, qui est parfois identifiée à la géométrie inversive (du plan euclidien). Cependant, la géométrie inversive est l'étude la plus large puisqu'elle inclut l'inversion brute dans un cercle (pas encore faite, avec conjugaison, en va-et-vient). La géométrie inverse comprend également la cartographie de conjugaison. Ni la conjugaison ni l'inversion dans un cercle ne sont dans le groupe de Möbius car elles ne sont pas conformes (voir ci-dessous). Les éléments du groupe de Möbius sont des fonctions analytiques du plan entier et sont donc nécessairement conformes. Transformer des cercles en cerclesOn considère, dans le plan complexe, le cercle de rayon autour du point où sans perte de généralité, En utilisant la définition de l'inversion on peut montrer directmeent que vérifie l'équation et donc que décrit le cercle de centre et rayon Lorsque le cercle se transforme en la droite parallèle à l'axe imaginaire Pour et le résultat pour est montrant que le décrit le cercle de centre et rayon . Lorsque l'équation pour devient Géométrie de dimensions supérieuresComme mentionné ci-dessus, l'origine nécessite une attention particulière dans la projection d'inversion de cercle. L'approche consiste à joindre un point à l'infini noté ∞ ou 1/0 . Dans l'approche des nombres complexes, où la réciprocité est l'opération apparente, cette procédure conduit à la droite projective complexe, souvent appelée la sphère de Riemann. Ce sont des sous-espaces et des sous-groupes de cet espace et groupe de mappages qui ont été appliqués pour produire les premiers modèles de géométrie hyperbolique par Beltrami, Cayley et Klein. Ainsi, la géométrie inversive inclut les idées de Lobachevski et Bolyai dans leur géométrie plane. De plus, Klein est tellement conquis par cette facilité des cartographies à identifier les phénomènes géométriques qu'il livre un manifeste, le programme d'Erlangen, en 1872. Depuis lors, de nombreux mathématiciens réservent le terme géométrie à un espace avec un groupe de cartographies de cet espace. Les propriétés significatives des figures dans la géométrie sont celles qui sont invariantes sous ce groupe. Par exemple, Smogorzhevsky [6] développe plusieurs théorèmes de géométrie inversive avant de commencer la géométrie lobachevskienne. Dans des dimensions supérieuresDans un espace à n dimensions où il y a une sphère de rayon r, l'inversion dans la sphère est donnée par La transformation par inversion en hyperplans ou hypersphères dans En peut être utilisée pour générer des dilatations, des translations ou des rotations. En effet, deux hypersphères concentriques, utilisées pour produire des inversions successives, entraînent une dilatation ou une contraction au centre des hypersphères. Une telle application s'appelle une similarité. Lorsque deux hyperplans parallèles sont utilisés pour produire des réflexions successives, le résultat est une translation. Lorsque deux hyperplans se coupent dans un (n –2) -hyperplan, les réflexions successives produisent une rotation où chaque point du (n –2)-hyperplan est un point fixe de chaque réflexion et donc de la composition. Ce sont toutes des applications conformes et, en fait, lorsque l'espace a trois dimensions ou plus, les applications générées par inversion sont les seules applications conformes. Le théorème de Liouville est un théorème classique de géométrie conforme. L'ajout d'un point à l'infini à l'espace évite la distinction entre hyperplan et hypersphère ; la géométrie inversive de dimension supérieure est alors fréquemment étudiée dans le contexte présumé d'une n -sphère comme espace de base. Les transformations de la géométrie inversive sont souvent appelées transformations de Möbius. La géométrie inverse a été appliquée à l'étude des colorations, ou partitionnements, d'une n-sphère[7]. Propriété de projection anti-conformeL'image d'inversion de cercle est anti-conforme, ce qui signifie qu'en tout point elle conserve les angles et inverse l'orientation (une carte est dite conforme si elle conserve les angles orientés ). Algébriquement, une application est anti-conforme si en tout point le jacobien est un scalaire multiplié par une matrice orthogonale à déterminant négatif : en deux dimensions le jacobien doit être un scalaire multiplié par une réflexion en tout point. Cela signifie que si J est le jacobien, alors et Calcul du Jacobien dans le cas zi = xi/|x|2, où |x|2 = x12 + ... + xn2 donne JJT = kI, avec k = 1/|x|4, et de plus det( J ) est négatif ; donc la carte inversive est anticonforme. Dans le plan complexe, l'application d'inversion de cercle la plus évidente (c'est-à-dire utilisant le cercle unité centré à l'origine) est le complexe conjugué de l'application complexe inverse prenant z en 1/ z . L'application inverse analytique complexe est conforme et son conjugué, l'inversion de cercle, est anti-conforme. Dans ce cas, une homographie est conforme tandis qu'une anti-homographie est anti-conforme. Géométrie inverse et géométrie hyperboliqueLa (n − 1)-sphère d'équation aura un rayon positif si a2 Par conséquent, il sera invariant par inversion si et seulement si c = 1. Mais cette condition correspond à l'orthogonalité avec la n-sphère unité. On est donc amené à considérer les (n − 1)-sphères d'équation qui sont invariantes par inversion, orthogonales à la sphère unité, et ont des centres en dehors de la sphère. Cellesx-ci, avec les hyperplans de sous-espace séparant les hémisphères, sont les hypersurfaces du modèle de disque de Poincaré en géométrie hyperbolique. Puisque l'inversion par la sphère unité laisse les sphères orthogonales à elle invariantes, l'inversion envoie les points à l'intérieur de la sphère unitaire vers l'extérieur et vice-versa. Ceci est donc vrai en général des sphères orthogonales, et en particulier l'inversion dans l'une des sphères orthogonales à la sphère unité envoie la sphère unité sur elle-même. Il projette également l'intérieur de la sphère unité sur elle-même, avec des points à l'extérieur de la sphère orthogonale envoyée à l'intérieur, et vice versa ; ceci définit les réflexions du modèle de disque de Poincaré si l'on y inclut également les réflexions à travers les diamètres séparant les hémisphères de la sphère unité. Ces réflexions génèrent le groupe d'isométries du modèle, qui nous indique que les isométries sont conformes. Par conséquent, l'angle entre deux courbes dans le modèle est le même que l'angle entre deux courbes dans l'espace hyperbolique. Voir aussi
Références
Notes et références
Liens externes
|
Portal di Ensiklopedia Dunia




































![{\displaystyle {\begin{aligned}&ww^{*}-{\frac {aw+a^{*}w^{*}}{(a^{*}a-r^{2})}}+{\frac {aa^{*}}{(aa^{*}-r^{2})^{2}}}={\frac {r^{2}}{(aa^{*}-r^{2})^{2}}}\\[4pt]\Longleftrightarrow {}&\left(w-{\frac {a^{*}}{aa^{*}-r^{2}}}\right)\left(w^{*}-{\frac {a}{a^{*}a-r^{2}}}\right)=\left({\frac {r}{\left|aa^{*}-r^{2}\right|}}\right)^{2}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9aa6efc01b1fd1b842804099c2595fcb27ea2ee0)



![{\displaystyle {\begin{aligned}&aw+a^{*}w^{*}=1\Longleftrightarrow 2\operatorname {Re} \{aw\}=1\Longleftrightarrow \operatorname {Re} \{a\}\operatorname {Re} \{w\}-\operatorname {Im} \{a\}\operatorname {Im} \{w\}={\frac {1}{2}}\\[4pt]\Longleftrightarrow {}&\operatorname {Im} \{w\}={\frac {\operatorname {Re} \{a\}}{\operatorname {Im} \{a\}}}\cdot \operatorname {Re} \{w\}-{\frac {1}{2\cdot \operatorname {Im} \{a\}}}.\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2b252d9984bc3b1ce123df34bd78d93f6c3accef)





