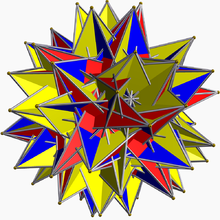
|
Grand icosidodécaèdre rétroadouci  Certaines informations figurant dans cet article ou cette section devraient être mieux reliées aux sources mentionnées dans les sections « Bibliographie », « Sources » ou « Liens externes » (). Vous pouvez améliorer la vérifiabilité en associant ces informations à des références à l'aide d'appels de notes.  Cet article est une ébauche concernant la géométrie. Vous pouvez partager vos connaissances en l’améliorant (comment ?) selon les recommandations des projets correspondants. Grand icosidodécaèdre rétroadouci
En géométrie, le grand icosidodécaèdre rétroadouci est un polyèdre uniforme non convexe, indexé sous le nom U74. Coordonnées cartésiennesLes coordonnées cartésiennes des sommets d'un grand icosidodécaèdre rétroadouci centré à l'origine sont les permutations paires de
avec un nombre pair de signes plus, où
et
où τ = (1+√5)/2 est le nombre d'or (quelquefois écrit φ) et ξ est la plus petite solution positive réelle de ξ³−2ξ=−1/τ, ou approximativement 0,3264046. En prenant les permutations impaires des coordonnées ci-dessus avec un nombre impair de signes plus, cela donne une autre forme, l'énantiomorphe de ce polyèdre. Voir aussiLien externeRobert Ferréol, « GRAND ICOSIDODÉCAÈDRE RÉTROADOUCI », sur Encyclopédie des formes mathématiques remarquables |
