|
Génétique quantitativeLa génétique quantitative est la génétique des caractères qui peuvent donner lieu à des mesures, que ce soient des caractères à variation continue[1] (tels que le poids ou la taille d'un organisme) ou discontinue (à déterminisme complexe), c'est-à-dire résultant de plusieurs facteurs génétiques ou non (on parle également de génétique multifactorielle)[2]. La génétique quantitative s’appuie sur la génétique des populations et les statistiques. HistoireGregor Mendel avait observé que, chez le haricot, le croisement de variétés à fleurs blanches et à fleurs rouges donnait « toute une série de couleurs allant du pourpre au violet pâle et blanc ». Pour expliquer ce phénomène, Mendel proposa de considérer que la couleur de la fleur du haricot est un mélange de caractères élémentaires, la transmission de chacun suivant les mêmes règles que celles mises en évidence chez le pois, suggérant ainsi ce qu’aujourd’hui nous décrivons comme l’intervention de plusieurs locus pour rendre compte de la variation continue de certains caractères. Plus tard, des sélectionneurs de plantes comme l’Américain East (1903) ou le Suédois Nielson Ehle (1908) firent des expériences étayant cette hypothèse multifactorielle. Il fallut cependant attendre 1918 pour que le statisticien anglais Ronald Fisher propose un modèle de synthèse, rendant à la fois compte des lois de Mendel et des relations biométriques entre apparentés. Au cours des années 1930 et 1940, la théorie synthétique de l'évolution a posé les bases de l'étude scientifique des processus d'évolution en biologie. Cette théorie est basée sur l'intégration de la théorie de l'hérédité mendélienne et de la génétique des populations à la théorie darwinienne. Cette théorie est aussi appelée néodarwinisme ou synthèse néodarwinienne pour souligner le fait qu'elle constitue une extension de la théorie originale de Charles Darwin, laquelle ignorait les mécanismes de l'hérédité génétique. L'analyse de locus de caractères quantitatifs (QTL) est un ajout plus récent à l'étude de la génétique quantitative. Principe de baseLa valeur phénotypique (P) d'un individu[3], c'est-à-dire le résultat de la mesure effectuée sur un individu, est modélisée de manière simplifiée (en ignorant les interactions entre génotypes et environnements) comme la somme d'une composante génétique appelée valeur génotypique (G) et d'une composante environnementale traduisant l'effet de l'environnement (E), soit :
L'effet environnemental désigne le milieu dans lequel vit (ou a vécu) l’individu observé, certains états physiologiques qui lui sont propres et l’observateur lui-même. En production végétale, on range dans cette catégorie des facteurs tels que l’année (influence du climat), la parcelle (influence des conditions topographiques et de sol), les doses d’engrais appliquées aux différents stades du développement de la plante, les traitements phytosanitaires effectués, les conditions de récolte, etc. Gènes marqueurs et gènes majeursAu lieu de repérer l’origine du génome des individus chromosome par chromosome, on peut le faire sur des fragments chromosomiques plus petits grâce au marqueurs génétiques moléculaires (RFLP, AFLP, microsatellites, SNP, etc.). Pour que l’action d’un gène soit facilement décelable, il faut que les différences induites par ce gène soient grandes en regard de la variation totale observée. De tels gènes sont appelés gènes majeurs, du fait de l’ampleur des différences phénotypiques qu'ils occasionnent. Dans de nombreuses espèces domestiques, l’existence de gènes majeurs pour certains caractères quantitatifs a pu être décelée par analyse des distributions. Cependant, des analyses fines de génétique quantitative mettent en évidence une composante autre que celle relative aux locus concernés. Génétique quantitative multivariéeLes traits phénotypiques partagent souvent certaines bases génétiques, et la covariance génétique additive parmi les traits les empêche d’évoluer indépendamment les uns des autres. La covariance résulte des processus d’épistasie et de déséquilibre de liaison. Ces processus génétiques donnent lieu à des patrons développementaux modulaires et à une intégration fonctionnelle, ce qui résulte en une sélection corrélée qui mène à une intégration génétique (corrélations génétiques). Finalement, la corrélation génétique aboutit à l’intégration évolutive et l’évolution corrélée des traits[4]. La génétique quantitative multivariée permet d’étudier l’évolution des traits en intégrant ces notions. La matrice G représente l’outil de base utilisé en génétique quantitative multivariée. Il s’agit du concept central pour comprendre la transmission d’une série de traits. L'utilisation de la génétique quantitative en évolutionBien que la génétique quantitative s’appuie sur l’étude des gènes entre des populations, de nombreuses études cherchent à relier la microévolution à la macroévolution, dans le but d’étudier la divergence des patrons de covariance[5]. Certains chercheurs constatent l’émergence d’une nouvelle discipline, la génétique quantitative comparative, qui se base sur la comparaison des variances et des covariances génétiques, mais qui se distingue de la génétique quantitative classique de par l’incorporation d’informations phylogénétiques par l’utilisation de la méthode comparative[6]. Définition et structure de la matrice G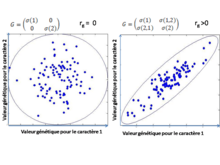 Une matrice G, ou matrice de variance-covariance génétique additive, est une matrice qui contient les valeurs de covariance génétique additive entre une suite de traits. C’est une matrice carrée symétrique qui contient sur sa diagonale les valeurs de variance génétique additive pour chaque trait étudié, et dont le coefficient σij contient la valeur de la covariance génétique additive entre les traits i et j.[1] Chaque individu dans une population possède une valeur génétique pour chaque trait phénotypique qui est transmis à la descendance. Il est possible de visualiser ces valeurs génétiques sous la forme d’un nuage de points, formant une ellipse. Ce nuage peut être représenté à l’aide d’une matrice G : les vecteurs propres de l’ellipse représentent les composantes principales, ou vecteurs propres, de la matrice G, et la longueur de chaque axe est déterminée à l’aide de la valeur propre correspondante de la matrice G. Plus exactement, la distance le long de chaque axe, en partant du centre de l’ellipse jusqu'à son extrémité est 1.96 fois égale à la racine carrée de la valeur propre correspondante. L'axe de l’ellipse le plus long est particulièrement intéressant car il représente la dimension dans l’espace des traits pour laquelle il y a le maximum de variance génétique. Cette dimension est parfois appelée la ligne de moindre résistance. Plus la corrélation génétique entre les traits est forte, plus l'ellipse est aplatie, et donc plus la ligne de moindre résistante est long par rapport aux deuxième axe[7]. L’étude des vecteurs propres et valeurs propres de la matrice G par les méthodes d’« analyse propre » (eigenanalysis), ou analyse en composantes principales (ACP) est utile car lorsque le nombre de traits mesuré augmente – donc la taille de la matrice – il est de plus en plus difficile d’interpréter des patrons de covariance simplement à l’aide de la matrice G. L’analyse propre facilite l’étude qualitative et la détermination statistique du potentiel évolutif ou de la base génétique d’une suite de traits[8]. L’influence de la matrice G sur la trajectoire évolutive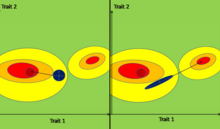 La matrice G joue un rôle crucial dans la théorie de l’évolution des traits polygéniques. Plusieurs études estiment qu’elle représente une contrainte évolutive, qui influencerait la trajectoire évolutive de concert avec le paysage adaptatif. En effet, lorsque la covariance entre certains traits est non nulle, l’évolution de la moyenne phénotypique prend une direction qui n’est souvent pas celle favorisée par la sélection[6]. La génétique quantitative donne des moyens de prédire l’évolution de suites de traits à partir de la connaissance de la sélection directionnelle et du degré de ressemblance parmi les individus de la population étudiée. Cette relation est donnée par l’« équation du sélectionneur » (breeder’s equation) et peut être étendue à plusieurs traits à travers l’équation de Lande (1979) nommée Multivariate breeder’s equation. Cette équation est une variante de la breeder’s equation étendue à plusieurs variables. Il s’agit de l’équation phare de la génétique quantitative multivariée[6]. Elle est décrite comme suit :
Δz est le vecteur représentant la variation de la moyenne phénotypique pour chaque trait. G représente la matrice de variance-covariance génétique additive. P représente la matrice de variance-covariance phénotypique, mesurée pour une population donnée en tenant compte des contributions génétiques et environnementales. S est le vecteur de covariance entre les traits et la valeur sélective, qui décrit l’action de la sélection sur l’évolution de la moyenne phénotypique. On peut également poser :
avec β le gradient de sélection, le vecteur contenant les coefficients de régression partielle de la valeur sélective pour chaque trait[6]. Cette équation a été utilisée dans des études théoriques pour explorer les trajectoires évolutives, notamment par l’étude des contraintes sur la direction de la trajectoire évolutive. La matrice G contraint la vitesse et la direction de l’adaptation. Si la matrice G est stable, elle pourrait être utilisée pour prédire le potentiel évolutif d’une population ou pour reconstruire la forme de sélection qui a mené à la divergence génétique au sein des populations, et par la suite parmi les espèces[8]. L'hypothèse comme quoi la matrice G agirait comme une contrainte évolutive sur une grande échelle de temps se traduirait par le fait qu'une forte corrélation génétique parmi des traits dans une espèce ancestrale engendrerait une forte corrélation entre la moyenne phénotypique de ces traits chez les espèces descendantes de l'espèce ancestrale. À l'inverse, une corrélation génétique presque nulle dans une espèce ancestrale ne contraindrait pas les possibilités d'évolution pour la descendances[5]. Aucun consensus empirique n'a pour l'instant émergé quant à l'importance de la matrice G en tant que contrainte évolutive[5]. Évolution théorique de la matrice GL’étude de la matrice G progresse beaucoup depuis ces dernières années. Jusqu’à présent, l’intérêt dans l’estimation de la matrice G se concentre sur l’étude de son évolution, plutôt que sur son exploitation comme outil pour étudier l’évolution phénotypique. En effet, la compréhension de la maintenance de la variation adaptative pour des traits est une question cruciale en biologie évolutive. De plus, ces études reflètent le souci de la validité des exploitations théoriques de la matrice G pour prédire l’évolution phénotypique : l’équation du sélectionneur multivariée ne peut être exploitée que si la matrice G est stable, ou si son évolution est prédictible et lente[5]. Cependant, il existe clairement des cas pour lesquels les matrices G ou certains de leurs éléments sont différents entre certaines populations, ce qui contredit l’hypothèse de la constance de la matrice G. Afin de comprendre l’évolution de la matrice G, des études tentent de prédire son comportement vis-à-vis de différents forces qui s’exercent sur elle. Des considérations théoriques font ressortir les hypothèses principales quant à l’impact des forces évolutives : Effets de la sélection : La sélection, surtout stabilisante, « grignote » le nuage de points modélisé par la matrice G à chaque génération. L’effet immédiat de cette sélection s'observe à l’échelle d’une génération et a tendance à diminuer la taille du nuage en changeant éventuellement sa forme et son orientation. Les effets les plus importants causés par la sélection devraient survenir là où la courbure du paysage adaptatif est la plus grande, car c'est là que la concentration des valeurs quantitatives est la plus forte[7]. Effets de la dérive génétique : dans une population finie, à chaque nouvelle génération la taille de l’ellipse devrait en moyenne diminuer sans changement dans sa forme ni son orientation[7]. En réponse à la dérive génétique, la matrice G évolue en théorie d'une génération à l'autre en restant proportionnelle à la matrice d'origine[9]. Effets des mutations : Les mutations constituent la force opposée qui contrebalance les effets de réduction de l'épaisseur de l'ellipse causés par la sélection et par la dérive génétique. Les mutations ont tendance à élargir la taille de l'ellipse[7]. Effets des migrations : Une étude de Guillaume et Whitlock (2007) cherche à identifier les effets de la migration, et postule que l’effet des migrations dépend de la force et de la direction du mouvement du paysage adaptatif. En effet, si une population isolée sur une île est exposée à de fortes migrations de populations en provenance d’un plus grand habitat avec un autre pic adaptatif, ces migrations influenceront l’évolution et la stabilité de la matrice G. Une forte migration peut stabiliser la matrice G si le mouvement du pic adaptatif durant la différentiation île-habitât principal suit la direction sélective de moindre résistance. Dans ces conditions, la migration conduit à l’amincissement de l’ellipse modélisée par la matrice G. À l’inverse, la migration peut aussi déstabiliser la matrice G si le mouvement du pic est perpendiculaire à la ligne de moindre résistance. Dans ce cas, l'ellipse est sujette à un épaississement et à une rotation[7]. En résumé, on peut imaginer la G-ellipse en équilibre oscillant stochastiquement en taille et en forme à la suite des forces exercées par la sélection, la dérive génétique et les mutations. Il est important de considérer les différentes échelles d’évolution de la matrice G. D’une part, à l’échelle d’une génération, la matrice G oscille en réponse aux forces qui s’exercent sur elle, même après qu’elle a atteint un équilibre sous l'effet de ces forces. Sur une échelle de temps plus longue, la matrice G pourrait évoluer en réponse à un changement de régime de sélection, c’est-à-dire un nouveau paysage adaptatif, et atteindre un nouvel état d’équilibre. Sur une échelle de temps encore plus grande, la matrice M, c’est-à-dire la matrice qui décrit les effets de nouvelles mutations sur les variances et covariances, est susceptible d’évoluer, influençant ainsi également l’évolution de la matrice G, qui tendrait vers un compromis entre le paysage adaptatif et la matrice M. De nombreuses études suggèrent que l’évolution de la matrice G est lente, ce qui assurerait son exploitation dans la prédiction de la trajectoire évolutive[7]. Les approches visant à l'étude de l'évolution de la matrice GLes approches analytiquesL’étude analytique de l’évolution de la matrice G : Les études analytiques n’ont jusqu’à présent pas été concluantes pour montrer l’impact des différentes forces évolutives sur la matrice G. La caractérisation de la matrice-G soumise à un régime statique de sélection, mutation et recombinaison n’a été accomplie que sous des combinaisons d’hypothèses simplifiant le modèle[7]. Les approches empiriquesLes approches empiriques utilisées pour étudier l’évolution de la matrice G consistent en la comparaison des matrices obtenues soit à partir d’échantillons naturels, soit par des traitements expérimentaux[7]. La comparaison de matrices obtenues à partir de populations naturelles a l’avantage de refléter les configurations obtenues dans des conditions naturelles. Malgré le fait que l’historique de la sélection et la taille de la population sont souvent inconnues, ces échantillons sont représentatifs du monde réel. Cependant, un inconvénient des études menées à partir d’échantillons naturels réside dans le fait que souvent seules deux ou trois matrices sont accessibles pour la comparaison, car il est difficile de récolter suffisamment d’échantillons de familles pour estimer G[7]. Du côté expérimental, les matrices G sont comparées après que des sous-populations ont été exposées à différents mutagènes, puis autorisées à dériver ou à croître. Cette approche permet de connaître la nature du traitement. Cependant, certaines forces naturelles qui pourraient agir sur la stabilité des vecteurs propres peuvent être absentes[7]. Les matrices G obtenues grâce à ces expériences ont souvent montré des aspects structurels conservés. En particulier, les vecteurs propres des matrices sont souvent conservés. Malgré ce fort signal de stabilité à travers de nombreuses comparaisons, certaines études ont aussi montré que la sélection, notamment celle associée à la radiation adaptative et à la radiation évolutive, peuvent donner des matrices G différentes, mais sur une échelle de temps courte[7]. Les approches par la simulationBien que les simulations informatiques de l’évolution des matrices G ne résolvent pas tous les problèmes concernant les comparaisons empiriques et leur interprétation, elles apportent des informations complémentaires pour l’étude de la stabilité et de l’évolution des matrices G. Elles peuvent notamment permettre de comprendre les forces responsables de la stabilité des vecteurs propres dans des études comparatives, ainsi que les pulsations erratiques de la matrice G qui peuvent survenir expérimentalement en l'absence de sélection[7]. Afin de générer plus facilement des résultats exploitables, ces études se concentrent généralement sur l’évolution de deux traits affectés par 10 à 100 loci pléiotropes. Malgré ces limitations, ces programmes permettent de simuler les processus de mutation, de sélection, de régulation de population, et de transmission des traits dans des populations comptant entre des centaines et des milliers d’individus sur des centaines de générations. Ces programmes sont conçus afin que les valeurs des paramètres pris en compte coïncident avec la théorie analytique, permettant ainsi de vérifier les résultats attendus et de les faire varier de façon réaliste afin de simuler les différentes forces évolutives, la taille des populations, etc.[7]. Ces études confirment les résultats obtenus avec les prédictions théoriques quant à l’évolution de la moyenne phénotypique. Elles suggèrent que la stabilité de la matrice G ne peut être obtenue que sous certaines conditions telles qu'une population de grande taille ainsi que des patrons de sélection corrélée forts et persistants coordonnés avec des patrons de mutations pléiotropes[7]. Un défi important dans l'étude de la matrice G consisterait à comprendre comment celle-ci évoluerait dans des systèmes avec une structure génétique plus réaliste, incluant les phénomènes de dominance et d'épistasie. Méthodes de comparaison des matrices GPlusieurs tests statistiques existent afin de comparer les matrices G entre différentes populations ou entre espèces. Il existe quatre types de méthodes statistiques principales permettant de comparer les matrices G : la comparaison élément par élément, la corrélation entre matrices, l’estimateur du maximum de ressemblance et la comparaison hiérarchique de Flury[9]. Les trois premières méthodes sont plus anciennes et très critiquées. En effet elles sont basées sur une hypothèse statistique nulle, ce qui rend l’interprétation des résultats compliquée. Le test de corrélation entre les matrices teste l’hypothèse nulle de non similitude entre matrices, tandis que la comparaison éléments par élément ou l’estimateur du maximum de ressemblance testent l’hypothèse nulle d’égalité entre les matrices ou d'une partie de leurs éléments[6]. La comparaison élément par élément consiste à tester séparément chaque élément des matrices. Cette méthode pose cependant problème car les éléments de la matrice ne sont pas indépendants les uns des autres et finalement trop de tests sont nécessaires pour rendre le pouvoir statistique suffisamment fort et les résultats exploitables. Malgré tout, cette méthode peut être utile comme méthode d’exploration des données afin de déterminer où résident les plus grandes différences[9]. Le test de corrélation entre matrices est le plus répandu, bien que certains articles remettent en question sa validité statistique. Un des inconvénients de cette approche est qu’elle ne permet pas de distinguer certaines des hypothèses qui sous-tendent ces études, comme par exemple les forces évolutives (sélection, dérive, mutations) responsables de la divergence entre matrices[9]. L’estimateur maximum de ressemblance est très populaire dans les analyses de génétique quantitative en général. Cette méthode permet d’estimer quelles parties de la matrice diffèrent et de combien, souvent par l’analyse séparée de sous-matrices. Ce test permet de questionner la ressemblance entre les matrices, mais ne permet pas de distinguer égalité, proportionnalité et autres différences entre les matrices[9]. La comparaison hiérarchique de Flury se base sur l’analyse des composantes principales communes. Elle est basée sur plusieurs hypothèses statistiques, et instaure une hiérarchie de similitude entre les matrices. En partant du haut de la pyramide, on distingue quatre critères de classification.
Cette méthode se base sur l’analyse des composantes principales communes (CPCA), qui récapitule toute la variation de jeu de données d’origine dans un nombre plus petit de vecteurs. L’analyse des composantes principales se base sur l’argument qui stipule que le changement évolutif influence la taille des valeurs propres correspondant aux composantes principales. Si une valeur propre vaut zéro, il n’y aura pas de variation génétique dans la direction associée au vecteur propre correspondant, et donc pas de changement évolutif. Une valeur propre très grande indique des traits très corrélés, et donc la sélection sera fortement influencée par la direction associée[9]. Références
|
Portal di Ensiklopedia Dunia

