|
Anneaux de Newton En optique, les anneaux de Newton désigne la figure d'interférence qui se forme lorsqu'une lentille plan-convexe de très faible courbure repose sur une lame plane en verre. En lumière monochromatique, on observe une série d'anneaux concentriques, alternativement lumineux et sombres, centrée sur le point de contact entre la surface sphérique de la lentille et la surface plane. En lumière blanche, il apparait une série d'anneaux concentriques aux couleurs de l'arc-en-ciel parce que les différentes longueurs d'onde interfèrent positivement ou négativement à différentes épaisseurs de la couche d'air entre la lentille et la plaque de verre. Le phénomène a d'abord été décrit par Robert Hooke dans son livre Micrographia (1665). Il porte le nom d'Isaac Newton, qui le décrit dans son ouvrage Opticks (1704), sans réussir à l'élucider dans son modèle corpusculaire de la lumière. Il a été expliqué dans le cadre de la théorie ondulatoire de la lumière, d'abord par Thomas Young en 1801[1], puis par Augustin Fresnel en 1815[2]. Réflexion et changement de phaseLorsque la lumière est réfléchie sur la surface d'un matériau d'indice de réfraction plus élevé que celui du milieu d'incidence, l'onde réfléchie est déphasée de π. Lorsque la lumière est réfléchie sur la surface d'un matériau d'indice moins élevé que celui du milieu d'incidence, l'onde est réfléchie sans déphasage. Lorsqu'une onde lumineuse monochromatique se propageant dans l'air (indice 1) frappe une lame de verre (indice 1,5), elle est partiellement réfléchie à l'interface air/verre avec un retard de phase de π et elle est partiellement réfractée sans modification de phase. Lorsque l'onde réfractée est réfléchie à son tour par la surface interne de la lame de verre (interface verre/air), elle est réfléchie sans déphasage. Si l'épaisseur de la lame est petite et de l'ordre de la longueur d'onde, les deux ondes réfléchies interfèrent et peuvent se détruire[3]. Si λ désigne la longueur d'onde, e, l'épaisseur de la plaque de verre, la différence de marche entre les deux rayons réfléchis s'écrit : Si , avec k entier positif ou nul, la différence de marche des deux rayons réfléchis sera : L'interférence est constructive si k est impair. L'interférence est destructrice si k est pair. Anneaux par réflexion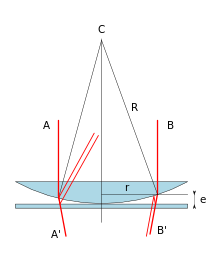 En incidence normale, par réflexion, la lumière pénètre la lentille plan convexe, est en partie réfléchie à l'interface verre/air, en partie réfractée dans l'espace rempli d'air entre la lentille et la plaque de verre, puis à nouveau répartie entre une réflexion et une réfraction au niveau de l'interface air/verre. Les deux rayons réfléchis interférent. Le rayon deux fois réfléchi a parcouru deux fois l'espace entre la lentille et le dioptre plan. Pour établir les équations de la marche des rayons lumineux il faut aussi tenir compte d'une observation de Young. Si λ désigne la longueur d'onde, e, la distance entre la surface courbe de la lentille et la surface plane réfléchissante, la différence de marche entre les deux rayons réfléchis s'écrit : Au niveau des anneaux lumineux, l'interférence des deux rayons est constructive. Leur différence de marche doit être constituée d'un nombre entier de longueurs d'onde : Au niveau des anneaux sombres, l'interférence des deux rayons est destructrice. Leur différence de marche doit donc être constituée d'un nombre impair de demies longueurs d'onde :  Avec k entier ou nul. D'où il vient, pour les anneaux sombres : L'épaisseur e de la couche d'air peut être exprimé en fonction du rayon R de courbure de la lentille et de la distance r entre l'axe de la lentille et le point d'incidence du rayon lumineux : Comme r << R, on peut négliger le terme . Il vient alors : Le rayon de l'anneau sombre d'ordre k : Au point de contact de la lentille et de la lame de verre, , et . Les deux rayons réfléchis sont en opposition de phase. On peut constater sur la figure 2 que le centre est sombre. Pour k = 1, 2, 3 ..., les anneaux sombres successifs correspondent aux interférences destructives du 1er, 2ème, 3ème ordre... Anneaux par transmissionFresnel explique l'apparence inversée des anneaux vus par transmission : là où il y a de l'ombre par réflexion, il y a de la lumière par transmission. En effet, la double réflexion introduit deux inversions de phase, ce qui retarde l'onde deux fois réfléchie d'une longueur d'onde par rapport à l'onde transmise directement (BB'). Les deux ondes sont donc en interférence constructive[2].  Leur différence de marche s'écrit : Au niveau des anneaux lumineux, l'interférence des deux rayons est constructive si leur différence de marche est constituée d'un nombre entier de longueurs d'onde : Avec k entier positif. D'où il vient, pour les anneaux lumineux : Avec k entier positif ou nul. Le rayon de l'anneau lumineux d'ordre k : Au point de contact de la lentille et de la lame de verre, , et . Le rayon direct et le rayon deux fois réfléchi sont en de phase. On peut constater sur la figure 3 que le centre est éclairé. Pour k = 1, 2, 3 ..., les anneaux lumineux successifs correspondent aux interférences constructives du 1er, 2ème, 3ème ordre... Le rayon des anneaux lumineux observés par transmission est le même que celui des anneaux sombres observés par réflexion. Notes et références
Liens externes |
Portal di Ensiklopedia Dunia


















