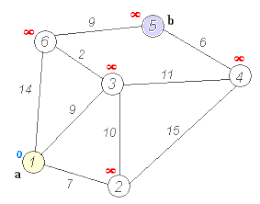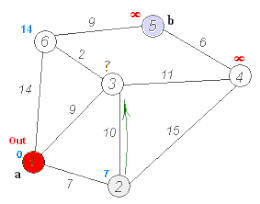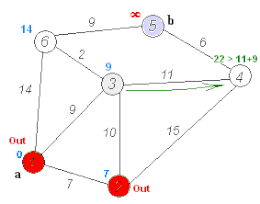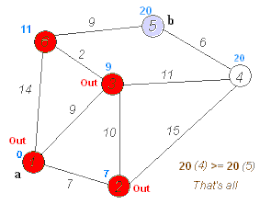
Algorithme de Dijkstra

Algorithme de Dijkstra

L'algorithme de Dijkstra pour trouver le chemin le plus court entre a et b. Il choisit le sommet non visité avec la distance la plus faible, calcule la distance à travers lui à chaque voisin non visité, et met à jour la distance du voisin si elle est plus petite. Il marque le sommet visité (en rouge) lorsqu'il a terminé avec les voisins.

Découvreur ou inventeur	Edsger Dijkstra
Date de découverte	1959[1]
Problèmes liés	Algorithme de recherche de chemin (d), algorithme de la théorie des graphes (en), algorithme glouton, algorithme
Structure des données	Graphe
Basé sur	Algorithme de parcours en largeur
À l'origine de	Algorithme A*, link-state routing protocol (en), Open Shortest Path First, IS-IS

Complexité en temps

Pire cas	Pour un graphe à ${\displaystyle n}$ sommets et ${\displaystyle m}$ arcs : ${\displaystyle O((n+m)\log(n))}$ pour l'implémentation avec un tas binaire, ${\displaystyle O(m+n\log(n))}$ pour l'implémentation avec un tas de Fibonacci

modifier - modifier le code - modifier Wikidata

En théorie des graphes, l'algorithme de Dijkstra (prononcé [dɛɪkstra]) sert à résoudre le problème du plus court chemin. Il permet, par exemple, de déterminer un plus court chemin pour se rendre d'une ville à une autre connaissant le réseau routier d'une région. Plus précisément, il calcule des plus courts chemins à partir d'une source vers tous les autres sommets dans un graphe orienté pondéré par des réels positifs. On peut aussi l'utiliser pour calculer un plus court chemin entre un sommet de départ et un sommet d'arrivée.

L'algorithme porte le nom de son inventeur, l'informaticien néerlandais Edsger Dijkstra, et a été publié en 1959[2].

Cet algorithme est de complexité polynomiale. Plus précisément, pour ${\displaystyle n}$ sommets et ${\displaystyle a}$ arcs, le temps est en ${\displaystyle O((a+n)\log n)}$, voire en ${\displaystyle O(a+n\log n)}$.

Problème du plus court chemin

L'algorithme de Dijkstra permet de résoudre un problème algorithmique : le problème du plus court chemin. Ce problème a plusieurs variantes. La plus simple est la suivante : étant donné un graphe non-orienté, dont les arêtes sont munies de poids, et deux sommets de ce graphe, trouver un chemin entre les deux sommets dans le graphe, de poids minimum. L'algorithme de Dijkstra permet de résoudre un problème plus général : le graphe peut être orienté, et l'on peut désigner un unique sommet, et demander d'avoir la liste des plus courts chemins pour tous les autres nœuds du graphe.

Principe sur un exemple

L'algorithme prend en entrée un graphe orienté pondéré par des réels positifs et un sommet source. Il s'agit de construire progressivement un sous-graphe dans lequel sont classés les différents sommets par ordre croissant de leur distance minimale au sommet de départ. La distance correspond à la somme des poids des arcs empruntés.

Au départ, on considère que les distances de chaque sommet au sommet de départ sont infinies, sauf pour le sommet de départ pour lequel la distance est nulle. Le sous-graphe de départ est l'ensemble vide.

Au cours de chaque itération, on choisit en dehors du sous-graphe un sommet de distance minimale et on l'ajoute au sous-graphe. Ensuite, on met à jour les distances des sommets voisins de celui ajouté. La mise à jour s'opère comme suit : la nouvelle distance du sommet voisin est le minimum entre la distance existante et celle obtenue en ajoutant le poids de l'arc entre sommet voisin et sommet ajouté à la distance du sommet ajouté.

On continue ainsi jusqu'à épuisement des sommets (ou jusqu'à sélection du sommet d'arrivée).

Distance entre la ville A et la ville J

Animation d'un algorithme de Dijkstra

Étape 1 : on choisit la ville A. On met à jour les villes voisines de A qui sont B, C, et E. Leurs distances deviennent respectivement 85, 217, 173, tandis que les autres villes restent à une distance infinie.

Étape 2 : on choisit la ville B. En effet, c'est la ville hors du sous-graphe qui est à la distance minimale (85). On met à jour le seul voisin (F). Sa distance devient 85+80 = 165.

Étape 3 : on choisit F. On met à jour le voisin I (415).

Étape 4 : on choisit E. On met à jour le voisin J (675).

Étape 5 : la distance la plus courte en dehors du sous-graphe est maintenant celle de la ville C. On choisit donc C. On met à jour la ville G (403) et la ville H (320).

Étape 6 : la distance la plus courte en dehors du sous-graphe est maintenant celle de la ville H (320). On choisit donc H. On met à jour la ville D (503) et la ville J (487< 675).

Étape 7 : la distance la plus courte suivante est celle de la ville G. On choisit G. La mise à jour ne change aucune autre distance.

Étape 8 : la distance la plus courte suivante est celle de la ville I. La distance de la ville voisine J n'est pas modifiée car la distance existante est inférieure à celle que l'on obtiendrait en passant par I (415 + 84 > 487).

Étape 9 : la ville dont la distance est la plus courte est J (487). On choisit J et on l'ajoute au sous-graphe. On s'arrête puisque la ville d'arrivée est maintenant dans le sous-graphe.

     

 

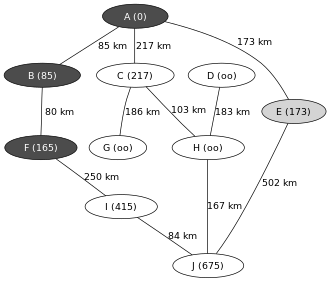
L'algorithme de Dijkstra fonctionne aussi sur un graphe non orienté. L'exemple ci-contre montre les étapes successives dans la résolution du chemin le plus court dans un graphe. Les nœuds symbolisent des villes identifiées par une lettre et les arêtes indiquent la distance entre ces villes. On cherche à déterminer le plus court trajet pour aller de la ville A à la ville J.

En neuf étapes, on peut déterminer le chemin le plus court menant de A à J, il passe par C et H et mesure 487 km.

Présentation sous forme de tableau

On peut aussi résumer l'exécution de l'algorithme de Dijkstra avec un tableau. Chaque étape correspond à une ligne. Une ligne donne les distances courantes des sommets depuis le sommet de départ. Une colonne donne l'évolution des distances d'un sommet donné depuis le sommet de départ au cours de l'algorithme. La distance d'un sommet choisi (car minimale) est soulignée. Les distances mises à jour sont barrées si elles sont supérieures à des distances déjà calculées.

Algorithme de Dijkstra

	à A	à B	à C	à D	à E	à F	à G	à H	à I	à J
étape initiale	0	∞	∞	∞	∞	∞	∞	∞	∞	∞
A(0)		85	217	∞	173	∞	∞	∞	∞	∞
B(85A)		-	217	∞	173	165	∞	∞	∞	∞
F(165B)		-	217	∞	173	-	∞	∞	415	∞
E(173A)		-	217	∞	-	-	∞	∞	415	675
C(217A)		-	-	∞	-	-	403	320	415	675
H(320C)		-	-	503	-	-	403	-	415	675 487
G(403C)		-	-	503	-	-	-	-	415	487
I(415F)		-	-	503	-	-	-	-	-	487
J(487H)		-	-	503	-	-	-	-	-	-
D(503H)		-	-	-	-	-	-	-	-	-

Le tableau donne non seulement la distance minimale de la ville A à la ville J (487) mais aussi le chemin à suivre à rebours (J - H - C - A) pour aller de A à J ainsi que toutes les distances minimales de la ville A aux autres villes rangées par ordre croissant.

Schéma de l'algorithme

Le graphe est noté ${\displaystyle G=(S,A)}$ où :

• l'ensemble ${\displaystyle S}$ est l'ensemble fini des sommets du graphe ${\displaystyle G}$ ;
• l'ensemble ${\displaystyle A}$ est l'ensemble des arcs de ${\displaystyle G}$ tel que : si ${\displaystyle (s_{1},s_{2})}$ est dans ${\displaystyle A}$, alors il existe un arc depuis le nœud ${\displaystyle s_{1}}$ vers le nœud ${\displaystyle s_{2}}$ ;
• on définit la fonction ${\displaystyle poids}$ définie sur ${\displaystyle S\times S}$ dans ${\displaystyle \mathbb {R} ^{+}\cup \{+\infty \}}$ qui à un couple ${\displaystyle (s_{1},s_{2})}$ associe le poids positif ${\displaystyle poids(s_{1},s_{2})}$ de l'arc reliant ${\displaystyle s_{1}}$ à ${\displaystyle s_{2}}$ (et ${\displaystyle +\infty }$ s'il n'y a pas d'arc reliant ${\displaystyle s_{1}}$ à ${\displaystyle s_{2}}$).

Le poids du chemin entre deux sommets est la somme des poids des arcs qui le composent. Pour une paire donnée de sommets ${\displaystyle s_{deb}}$ (le sommet du départ) ${\displaystyle s_{fin}}$ (le sommet d'arrivée) appartenant à ${\displaystyle S}$, l'algorithme trouve un chemin depuis ${\displaystyle s_{deb}}$ vers ${\displaystyle s_{fin}}$ de moindre poids (autrement dit un chemin le plus léger ou encore le plus court).

L'algorithme fonctionne en construisant un sous-graphe ${\displaystyle P}$ de manière que la distance entre un sommet ${\displaystyle s}$ de ${\displaystyle P}$ depuis ${\displaystyle s_{deb}}$ soit connue et soit un minimum dans ${\displaystyle G}$. Initialement, ${\displaystyle P}$ contient simplement le nœud ${\displaystyle s_{deb}}$ isolé, et la distance de ${\displaystyle s_{deb}}$ à lui-même vaut zéro. Des arcs sont ajoutés à ${\displaystyle P}$ à chaque étape :

1. en identifiant tous les arcs ${\displaystyle a_{i}=(s_{i1},s_{i2})}$ dans ${\displaystyle P\times G}$;

2. en choisissant l'arc ${\displaystyle a_{j}=(s_{j1},s_{j2})}$ dans ${\displaystyle P\times G}$ qui donne la distance minimum depuis ${\displaystyle s_{deb}}$ à ${\displaystyle s_{j2}}$ en passant tous les chemins créés menant à ce nœud.

L'algorithme se termine soit quand ${\displaystyle P}$ devient un arbre couvrant de ${\displaystyle G}$, soit quand tous les nœuds d'intérêt[3] sont dans ${\displaystyle P}$.

On peut donc écrire l'algorithme de la façon suivante :

Entrées : ${\displaystyle G=(S,A)}$ un graphe avec une pondération positive ${\displaystyle poids}$ des arcs, ${\displaystyle s_{deb}}$ un sommet de ${\displaystyle S}$

${\displaystyle P:=\emptyset }$
${\displaystyle d[a]:=+\infty }$ pour chaque sommet ${\displaystyle a}$
${\displaystyle d[s_{deb}]=0}$
Tant qu'il existe un sommet hors de ${\displaystyle P}$
    Choisir un sommet ${\displaystyle a}$ hors de ${\displaystyle P}$ de plus petite distance ${\displaystyle d[a]}$
    Mettre ${\displaystyle a}$ dans ${\displaystyle P}$ 
    Pour chaque sommet ${\displaystyle b}$ hors de  ${\displaystyle P}$ voisin de ${\displaystyle a}$
       Si d[b] > d[a] + poids(a, b)
           ${\displaystyle d[b]=d[a]+poids(a,b)}$
           prédécesseur[b] := a
    Fin Pour
Fin Tant Que

Implémentation de l'algorithme

Fonctions annexes

L'algorithme utilise les fonctions annexes suivantes.

Initialisation de l'algorithme

Initialisation(G,sdeb)
1 pour chaque point s de G faire
2    d[s] := infini             /* on initialise les sommets autres que sdeb à infini */[4]
3 fin pour
4 d[sdeb] := 0                  /* la distance au sommet de départ sdeb est nulle */

Recherche d'un nœud de distance minimale

• On recherche un nœud de distance minimale (relié par l'arc de poids le plus faible) de ${\displaystyle s_{deb}}$ parmi les nœuds situés hors de ${\displaystyle P}$. Le complémentaire de ${\displaystyle P}$ est noté ${\displaystyle Q}$. On implémente pour cela une fonction Trouve_min(Q) qui choisit un nœud de Q de distance minimale.

Trouve_min(Q)
1 mini := infini
2 sommet := -1
3 pour chaque sommet s de Q
4    si d[s] < mini
5    alors 
6        mini := d[s]
7        sommet := s
8 fin pour
9 renvoyer sommet

Mise à jour des distances

• On met à jour les distances entre ${\displaystyle s_{deb}}$ et ${\displaystyle s_{2}}$ en se posant la question : vaut-il mieux passer par ${\displaystyle s_{1}}$ ou pas ?

maj_distances(s1,s2)
1 si d[s2] > d[s1] + Poids(s1,s2)      /* Si la distance de sdeb à s2 est plus grande que */
2                                      /* celle de sdeb à S1 plus celle de S1 à S2 */
3    alors 
4        d[s2] := d[s1] + Poids(s1,s2) /* On prend ce nouveau chemin qui est plus court */
5        prédécesseur[s2] := s1        /* En notant par où on passe */

Fonction principale

Voici la fonction principale utilisant les précédentes fonctions annexes :

Dijkstra(G,Poids,sdeb)
1 Initialisation(G,sdeb)
2 Q := ensemble de tous les nœuds
3 tant que Q n'est pas un ensemble vide faire
4       s1 := Trouve_min(Q)
5       Q := Q privé de s1
6       pour chaque nœud s2 voisin de s1 faire
7           maj_distances(s1,s2)
8       fin pour
9 fin tant que

Le plus court chemin de ${\displaystyle s_{deb}}$ à ${\displaystyle s_{fin}}$ peut ensuite se calculer itérativement selon l'algorithme suivant, avec ${\displaystyle A}$ la liste représentant le plus court chemin de ${\displaystyle s_{deb}}$ à ${\displaystyle s_{fin}}$:

1 A := suite vide
2 s := sfin
3 tant que s != sdeb faire
4   A := cons(s, A)            /* on ajoute s en tête de la liste A */
5   s := prédécesseur[s]       /* on continue de suivre le chemin */
6 fin tant que
7 A := cons(sdeb, A)           /* on ajoute le nœud de départ */

Attention : s'il n'y a pas de chemin de ${\displaystyle s_{deb}}$ à ${\displaystyle s_{fin}}$ cette partie de l'algorithme fait une boucle infinie ou une erreur selon votre implémentation.

Spécialisation de l'algorithme

Il est possible de spécialiser l'algorithme en arrêtant la recherche lorsque l'égalité ${\displaystyle s_{1}=s_{fin}}$ est vérifiée, dans le cas où on ne cherche que la distance minimale entre ${\displaystyle s_{deb}}$ et ${\displaystyle s_{fin}}$.

Complexité de l'algorithme

L'efficacité de l'algorithme de Dijkstra repose sur une mise en œuvre efficace de Trouve_min. L'ensemble ${\displaystyle Q}$ est implémenté par une file à priorités. Si le graphe possède ${\displaystyle |A|}$ arcs et ${\displaystyle |S|}$ nœuds, qu'il est représenté par des listes d'adjacence et si on implémente la file à priorités par un tas binaire (en supposant que les comparaisons des poids d'arcs soient en temps constant), alors la complexité en temps de l'algorithme est ${\displaystyle O((|A|+|S|)\times \log(|S|))}$. En revanche, si on implémente la file à priorités avec un tas de Fibonacci, l'algorithme est en ${\displaystyle O(|A|+|S|\times \log(|S|))}$[5].

Correction de l'algorithme

La démonstration de correction est une récurrence sur Card(P) (qui augmente de 1 à chaque itération) et repose sur l'invariant suivant :

${\displaystyle {\begin{cases}\forall c\in P,\,d(c)=mini(c)\\\forall c\not \in P,\,d(c)=miniP(c)\end{cases}}}$

où :

• mini(c) est le poids d'un plus court chemin menant à c ;
• miniP(c) est le poids d'un plus court chemin dont tous les sommets intermédiaires sont dans P menant à c.

Si n = Card(P), la preuve est la suivante :

• pour n = 0 et 1 : immédiat ;
• pour n un entier non nul, supposons l'invariant vrai.

L'algorithme sélectionne un pivot ${\displaystyle a\not \in P}$ tel que ${\displaystyle d(a)={\underset {x\not \in P}{Min}}\,d(x)}$, et l'ajoute dans P. Il faut donc montrer que ${\displaystyle d(a)=mini(a)}$ après modification de P:

Par hypothèse, ${\displaystyle d(a)=miniP(a)}$ avant modification de P, donc s'il existe un chemin C tel que ${\displaystyle poids(C)<d(a)}$ alors ce chemin contient au moins un sommet b ${\displaystyle \neq }$ a tel que ${\displaystyle b\not \in P}$.

Soit donc un tel sommet b tel que tous ses prédécesseurs dans C soient dans P (il existe car le premier sommet de C est l'origine qui est dans P). Décomposons C en Cb- et Cb+ où Cb- est la première partie de C dont le dernier sommet est b, et Cb+ la suite de C. Alors ${\displaystyle poids(C)=poids(Cb-)+poids(Cb+)\geq poids(Cb-)=d(b)\geq d(a)}$ : contradiction.

Il n'existe donc aucun chemin C tel que ${\displaystyle poids(C)<d(a)}$ d'où ${\displaystyle d(a)=mini(a)}$. L'égalité est toujours vraie pour les autres éléments de P.

Enfin, l'algorithme met à jour la fonction d (et prédécesseur) pour les successeurs b du pivot a : ${\displaystyle d[b]=\min(d[b],d[a]+poids(a,b))}$.

Montrons qu'alors, ${\displaystyle \forall c\not \in P,\,d(c)=miniP(c)}$ :

• si c n'est pas un successeur du pivot a, alors il n'existe aucun nouveau chemin C menant à c tel que ${\displaystyle poids(C)<d(c)}$ et dont tous les sommets intermédiaires sont dans P après l'ajout de a dans P puisqu'il faudrait alors passer par a avant de passer par un autre sommet ${\displaystyle d\in P}$, mais ce ne serait pas le plus court chemin jusqu'à d puisque le poids du plus court chemin jusqu'à d a déjà été calculé avant l'ajout de a dans P par hypothèse, et ce chemin ne contient donc que des sommets ayant été dans P avant l'ajout de a dans P ;

• sinon, il existe de tels chemins, en notant C le meilleur d'entre eux, alors C sera un des nouveaux chemins engendrés par l'ingestion du pivot a par P, donc ${\displaystyle a\in C}$ et d'autre part le pivot a est le dernier sommet intermédiaire de C puisque le plus court chemin menant aux autres sommets de P ne passe par a comme expliqué plus haut. C est donc la réunion du plus court chemin menant à a avec l'arc (a, c) : d'où ${\displaystyle poids(C)=d(c)=poids((a,c))+d(a)=miniP(c)}$.

Applications

L'algorithme de Dijkstra trouve une utilité dans le calcul des itinéraires routiers. Le poids des arcs pouvant être la distance (pour le trajet le plus court), le temps estimé (pour le trajet le plus rapide), la consommation de carburant et le prix des péages (pour le trajet le plus économique). ^[réf. nécessaire]

Une application courante de l'algorithme de Dijkstra apparaît dans les protocoles de routage interne « à état de liens », tels que Open Shortest Path First (OSPF)[6] ou IS-IS[7] – ou encore PNNI (en) sur les réseaux ATM –, qui permettent un routage internet très efficace des informations en cherchant le parcours le plus efficace.^[réf. nécessaire]

Comparaison avec d'autres algorithmes

• L'algorithme de Dijkstra est fondé sur un parcours en largeur.
• La spécialisation de l'algorithme de Dijkstra qui calcule un plus court chemin d'une source à une destination est une instance de l'algorithme A* dans lequel la fonction heuristique est la fonction nulle. L'algorithme A* qui utiliserait une heuristique minorante et monotone (par exemple la distance à vol d'oiseau) peut être plus efficace ^[réf. souhaitée].
• L'algorithme ne s'applique pas aux graphes avec des poids négatifs. Mais l'algorithme de Bellman-Ford permet de résoudre le problème des plus courts chemins depuis une source avec des poids négatifs (mais sans cycle négatif).
• L'algorithme de Floyd-Warshall calcule des plus courts chemins entre tous les sommets dans un graphe où les poids peuvent être négatifs.

Notes et références

1. (en) E. W. Dijkstra, « A note on two problems in connexion with graphs », Numerische Mathematik, Springer Science+Business Media, vol. 1, n^o 1,‎ décembre 1959, p. 269-271 (ISSN 0029-599X et 0945-3245, OCLC 1760917, DOI 10.1007/BF01386390, lire en ligne).
2. Dijkstra, E. W., « A note on two problems in connexion with graphs », Numerische Mathematik, vol. 1,‎ 1959, p. 269–271 (DOI 10.1007/BF01386390.).
3. Par exemple, les nœuds n'ayant pas d'arêtes autres que celle que l'on a parcourue pour arriver à eux, ne sont pas considérés comme des nœuds d'intérêt.
4. La suite de caractères /* ... */ est un commentaire.
5. Cormen et al. 2010, p. 610
6. (en) John Moy, « RFC2328 OSPF Version 2 », avril 1998 (consulté le 19 mai 2016) : « Using the Dijkstra algorithm, a tree is formed from this subset of the link state database. », p. 161
7. (en) David R. Oran, « RFC1142 : OSI IS-IS Intra-domain Routing Protocol », février 1990 (consulté le 19 mai 2016) : « An algorithm invented by Dijkstra (see references) known as shortest path first (SPF), is used as the basis for the route calculation. »

Annexes

Bibliographie

• (en) « A short introduction to the art of programming » de Edsger W. Dijkstra, 1971, contenant l'article original (1959) décrivant l'algorithme de Dijkstra (pages 67 à 73).
• (en) Thomas H. Cormen, Charles E. Leiserson, Ronald L. Rivest et Clifford Stein, Introduction to Algorithms, MIT Press et McGraw-Hill, 2001, 2^e éd. [détail de l’édition], section 24.3, « Dijkstra's algorithm », pages 595–601.
• Thomas H. Cormen, Charles E. Leiserson, Ronald L. Rivest et Clifford Stein (trad. de l'anglais), Algorithmique : Cours avec 957 exercices et 158 problèmes, Dunod, 2010 [détail de l’édition]

Articles connexes

• Lexique de la théorie des graphes
• Recherche de chemin et Problèmes de cheminement
• Algorithme de parcours en largeur
• Algorithme A*
• Article sur l'algorithme de Ford-Bellman qui permet de calculer le plus court chemin avec des poids d'arcs négatifs

Liens externes

• Explication détaillée de l'algorithme de Dijkstra et implémentation complète en C++
• Explication détaillée de l'algorithme de Dijkstra et implémentation complète en Python
• (en) Applet Java montrant l'algorithme de Dijkstra étape par étape
• (en) Applets Java utilisant l'algorithme