Método de la transformada inversa

Método de la transformada inversa.

El método de la transformada (o transformación) inversa, también conocido como método de la transformada integral de probabilidad inversa,[1]​ es un método para la generación de números aleatorios de cualquier distribución de probabilidad continua cuando se conoce la inversa de su función de distribución (cdf). Este método es en general aplicable, pero puede resultar muy complicado obtener una expresión analítica de la inversa para algunas distribuciones de probabilidad. El método de Box-Muller es un ejemplo de algoritmo que aunque menos general, es más eficiente desde el punto de vista computacional.[2]​

El método se utiliza para simular valores de las distribuciones exponencial, Cauchy, triangular, de Pareto y Weibull.

Método

El problema que resuelve el método de la transformada inversa es el siguiente:

• Sea ${\displaystyle X}$ una variable aleatoria cuya distribución puede ser descrita por la función de distribución ${\displaystyle F_{X}}$.
• Se desea generar valores de ${\displaystyle X}$ que están distribuidos según dicha distribución.

El método de la transformada inversa funciona de la siguiente manera:

1. Se genera un número aleatorio ${\displaystyle u}$ a partir de la distribución uniforme en el intervalo ${\displaystyle (0,1)}$, esto es ${\displaystyle U\sim \operatorname {U} (0,1)}$.
2. Se halla la inversa de la función de distribución, esto es, ${\displaystyle F_{X}^{-1}(x)}$.
3. Calcular ${\displaystyle X=F_{X}^{-1}(u)}$, esta variable aleatoria ${\displaystyle X}$ tiene distribución ${\displaystyle F_{X}}$.

Expresado de manera diferente, dada una variable aleatoria continua ${\displaystyle U}$ en ${\displaystyle (0,1)}$ y una función de distribución invertible ${\displaystyle F_{X}}$, la variable aleatoria ${\displaystyle X=F_{X}^{-1}(U)}$ tiene distribución ${\displaystyle F_{X}}$.

La función inversa de ${\displaystyle y=F_{X}(x)}$ puede ser escrita como ${\displaystyle F_{X}^{-1}(y)=\inf\{x|F_{X}(x)\geq y\}}$.

Intuición

De ${\displaystyle U\sim \operatorname {U} (0,1)}$ queremos generar ${\displaystyle X}$ con función de distribución ${\displaystyle F_{X}}$, donde asumimos que ${\displaystyle F_{X}}$ es una función estrictamente creciente.

Queremos ver si podemos hallar una transformación estrictamente monótona ${\displaystyle T:[0,1]\to \mathbb {R} }$ tal que ${\displaystyle T(U){\overset {d}{=}}X}$ entonces tendremos

${\displaystyle {\begin{aligned}F_{X}(x)&=\operatorname {P} [X\leq x]\\&=\operatorname {P} [T(U)\leq x]\\&=\operatorname {P} [U\leq T^{-1}(x)]\\&=T^{-1}(x)\end{aligned}}}$

para ${\displaystyle x\in \mathbb {R} }$ donde en el último paso se utilizó que ${\displaystyle \operatorname {P} [U\leq y]=y}$ cuando ${\displaystyle U}$ es uniforme en ${\displaystyle (0,1)}$.

Entonces obtuvimos que ${\displaystyle F_{X}}$ es la inversa de la función ${\displaystyle T}$ o equivalentemente ${\displaystyle T(u)=F_{X}^{-1}(u),u\in [0,1]}$

Caso Continuo

Considérese que se desea generar una variable aleatoria continua ${\displaystyle X}$ con función de distribución ${\displaystyle F_{X}}$, para generar a ${\displaystyle X}$, se considera el método de la transformada inversa basado en el siguiente teorema.

Teorema

Sea ${\displaystyle U}$ una variable aleatoria uniforme en ${\displaystyle (0,1)}$, para cualquier función de distribución continua invertible ${\displaystyle F}$, la variable aleatoria ${\displaystyle X}$ definida como${\displaystyle X=F^{-1}(U)}$ tiene distribución ${\displaystyle F}$, donde ${\displaystyle F^{-1}}$ se define como el valor de ${\displaystyle x}$ tal que ${\displaystyle F(x)=u}$.

Demostración

Sea ${\displaystyle F_{X}}$ la función de distribución de ${\displaystyle X=F^{-1}(U)}$ entonces

${\displaystyle {\begin{aligned}F_{X}(x)&=\operatorname {P} [X\leq x]\\&=\operatorname {P} [F^{-1}(U)\leq x]\end{aligned}}}$

como ${\displaystyle F_{X}}$ es una función de distribución entonces ${\displaystyle F_{X}}$ es una función monótona creciente de ${\displaystyle x}$ entonces

${\displaystyle {\begin{aligned}F_{X}(x)&=\operatorname {P} [F^{-1}(U)\leq x]\\&=\operatorname {P} [F(F^{-1}(U))\leq F(x)]\\&=\operatorname {P} [U\leq F(x)]\\&=F(x)\end{aligned}}}$

Este teorema muestra que para generar una variable aleatoria ${\displaystyle X}$ a partir de la función de distribución continua ${\displaystyle F_{X}}$, generemos un número aleatorio ${\displaystyle U}$ y hacemos entonces ${\displaystyle X=F^{-1}(U)}$.

Caso Discreto

Supóngase que queremos generar el valor valor de una variable aleatoria discreta ${\displaystyle X}$ con función de probabilidad

${\displaystyle \operatorname {P} [X=x_{j}]=p_{j}}$

con ${\displaystyle j=0,1,2,\dots }$ y

${\displaystyle \sum _{j}p_{j}=1}$

Para esto, generamos un número aleatorio ${\displaystyle U}$, esto es, ${\displaystyle U\sim \operatorname {U} (0,1)}$ y se define

${\displaystyle X=\left\{{\begin{matrix}x_{0}&{\mbox{si}}&U<p_{0}\\x_{1}&{\mbox{si}}&p_{0}\leq U<p_{0}+p_{1}\\\vdots &\vdots &\vdots \\x_{j}&{\mbox{si}}&\displaystyle \sum _{i=1}^{j-1}p_{i}\leq U<\sum _{i=1}^{j}p_{i}\\\vdots &\vdots &\vdots \end{matrix}}\right.}$

Como ${\displaystyle \operatorname {P} [a\leq U<b]=b-a}$ para ${\displaystyle 0<a<b<1}$entonces

${\displaystyle \operatorname {P} [X=x_{j}]=\operatorname {P} \left[\sum _{i=1}^{j-1}p_{i}\leq U<\sum _{i=1}^{j}p_{i}\right]=p_{j}}$

por lo tanto ${\displaystyle X}$ tiene la distribución deseada.

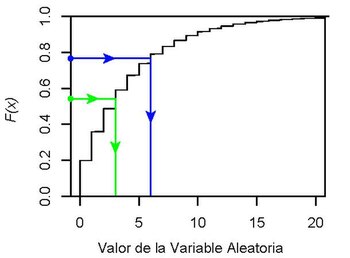
Ejemplo del método de la tranformada inversa para una variable aleatória geométrica discreta con ${\displaystyle p=0.2}$

Ejemplos

Ejemplo 1

Supóngase que se tiene una variable aleatoria ${\displaystyle U\sim \operatorname {U} (0,1)}$ y una función de distribución

${\displaystyle F(x)=1-\exp(-{\sqrt {x}})}$

Para poder aplicar el método, debemos resolver ${\displaystyle F(F^{-1}(u))=u}$

${\displaystyle {\begin{aligned}F(F^{-1}(u))&=u\\1-\exp \left(-{\sqrt {F^{-1}(u)}}\right)&=u\\F^{-1}(u)&=\left(-\ln(1-u)\right)^{2}\\&=(\ln(1-u))^{2}\end{aligned}}}$

a partir de aquí, ya podemos aplicar los pasos uno, dos y tres antes mencionados

Ejemplo 2

Si ${\displaystyle X}$ es una variable aleatoria exponencial con parámetro ${\displaystyle \lambda =1}$, esto es, ${\displaystyle X\sim \operatorname {Exponencial} (1)}$ entonces su función de distribución está dada por

${\displaystyle F_{X}(x)=1-e^{-x}}$

Si hacemos ${\displaystyle x=F^{-1}(u)}$ entonces

${\displaystyle u=F_{X}(x)=1-e^{-x}}$

esto es

${\displaystyle {\begin{aligned}u&=1-e^{-x}\\1-u&=e^{-x}\\x&=-\ln(1-u)\end{aligned}}}$

por lo tanto, para generar una variable aleatoria exponencial con parámetro ${\displaystyle \lambda =1}$, generamos un número aleatorio ${\displaystyle U}$ y hacemos

${\displaystyle X=F^{-1}(U)=-\ln(1-U)}$

Recordemos que si ${\displaystyle Y\sim \operatorname {U} (0,1)}$ entonces ${\displaystyle 1-Y\sim \operatorname {U} (0,1)}$, aplicando este resultado obtenemos

${\displaystyle X=F^{-1}(U)=-\ln(U)}$

a partir de aquí, ya podemos aplicar los pasos uno, dos y tres antes mencionados.

Véase también

• Cópula, definida por medio de una transformación de integral de probabilidad.
• Método de aceptación y rechazo
• Número pseudoaleatorio
• Generador lineal congruencial
• Variable aleatoria
• Función de distribución
• Distribución exponencial
• Distribución de Weibull
• Distribución de Pareto

Referencias

1. Aalto University, N. Hyvönen, Computational methods in inverse problems. Twelfth lecture https://noppa.tkk.fi/noppa/kurssi/mat-1.3626/luennot/Mat-1_3626_lecture12.pdf
2. Luc Devroye. Non-Uniform Random Variate Generation. New York: Springer-Verlag, 1986

Enlaces externos

• Transformación integral de probabilidad que define una copula condicional.

• Datos: Q1377019