|
Característica de Euler
En matemática y, en particular, en topología algebraica, la característica de Euler o característica de Euler-Poincaré es un invariante topológico, un número definido que sirve para describir la forma o la estructura de una clase de espacios topológicos. Es denotada generalmente por (la letra griega Ji). La característica de Euler se definió originalmente para poliedros y se usó para probar varios teoremas sobre ellos, incluida la clasificación de los sólidos platónicos, que se ha descubierto que figuraba en un manuscrito inédito de 1537 obra de Francesco Maurolico.[1] Leonhard Euler, por quien se nombra el concepto, lo introdujo para los poliedros convexos de manera más general, pero no pudo probar rigurosamente que es un invariante. Su conocida fórmula para los poliedros tiene la expresión siguiente: En las matemáticas modernas, la característica de Euler surge del concepto de homología y, de forma más abstracta, del álgebra homológica, habiéndose extendido a la caracterización de todo tipo de superficies. Característica de Euler en poliedrosLa característica de Euler de un politopo de tres dimensiones (poliedro) se puede calcular usando la fórmula siguiente: donde V, A y C son los números de vértices, de aristas y de caras, respectivamente. En particular, para cualquier poliedro homeomorfo a una esfera se tiene que Por ejemplo, para un cubo se cumple que 6 + 8 - 12 = 2 y para un tetraedro a su vez 4 + 4 - 6= 2. La fórmula anterior también se llama la fórmula de Euler, que se puede demostrar por inducción matemática o correspondencia sobre una esfera. Otros ejemplos se pueden encontrar en la siguiente tabla
Un poliedro que no sea homeomorfo a una esfera, como el poliedro toroidal de la figura, que tiene 48 caras, 22 vértices y 70 aristas, el resultado obtenido es 22 - 70 + 48 = 0. Tabla con las características de Euler de otros poliedros
Para poliedros regulares, Arthur Cayley derivó una forma modificada de la fórmula de Euler utilizando la densidad D, figura de vértice densidad dv, y densidad de cara : Esta versión vale tanto para poliedros convexos (donde las densidades son todas 1) como para los poliedros Kepler-Poinsot no convexos. Los poliedros proyectivos tienen todos característica de Euler 1, como el plano proyectivo real, mientras que las superficies de los poliedros toroidales tienen todas característica de Euler 0, como el toroide. Grafos planosVéase también: Grafo plano#Fórmula de Euler
La característica de Euler se puede definir para conectados grafo planos mediante la misma fórmula que para las superficies poliédricas, donde F es el número de caras del grafo, incluyendo la cara exterior. La característica de Euler de cualquier grafo plano conexo G es 2. Esto se demuestra fácilmente por inducción sobre el número de caras determinado por G, comenzando con un árbol como caso base. Para árboles, y . Si G tiene C componentes (grafos desconectados), el mismo argumento por inducción sobre F muestra que . Uno de los pocos trabajos de teoría de grafos de Cauchy también prueba este resultado. A través de la proyección estereográfica el plano mapea a la 2-esfera, de modo que un grafo conexo mapea a una descomposición poligonal de la esfera, que tiene característica de Euler 2. Este punto de vista está implícito en la prueba de Cauchy de la fórmula de Euler que se da a continuación. Demostración de la fórmula de Euler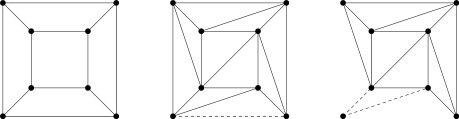 Hay muchas pruebas de la fórmula de Euler. Una fue dada por Cauchy en 1811, como sigue. Se aplica a cualquier poliedro convexo, y más generalmente a cualquier poliedro cuya frontera sea topológicamente equivalente a una esfera y cuyas caras sean topológicamente equivalentes a discos. Quitar una cara de la superficie poliédrica. Apartando entre sí las aristas de la cara que falta, deformar todo el resto en un grafo plano de puntos y curvas, de tal forma que el perímetro de la cara que falta se sitúe exteriormente, rodeando el grafo obtenido, como ilustra el primero de los tres grafos para el caso especial del cubo. (La suposición de que la superficie poliédrica es homeomórfica a la esfera al principio es lo que hace esto posible). Tras esta deformación, las caras regulares dejan de serlo en general. El número de vértices y aristas sigue siendo el mismo, pero el número de caras se ha reducido en 1. Por tanto, demostrar la fórmula de Euler para el poliedro se reduce a demostrar que V - E + F = 1 para este objeto deformado y plano. Si hay una cara con más de tres lados, dibuja una diagonal, es decir, una curva a través de la cara que conecta dos vértices que aún no están conectados. Cada nueva diagonal añade una arista y una cara y no cambia el número de vértices, por lo que no cambia la cantidad V - E + F (la suposición de que todas las caras son discos es necesaria aquí, para demostrar mediante el teorema de la curva de Jordan que esta operación aumenta el número de caras en uno). Continúa añadiendo aristas de esta manera hasta que todas las caras sean triangulares. Aplicar repetidamente cualquiera de las dos transformaciones siguientes, manteniendo el invariante de que la frontera exterior es siempre un ciclo simple:
Estas transformaciones acaban reduciendo el grafo plano a un único triángulo. (Sin el invariante de ciclo simple, eliminar un triángulo podría desconectar los triángulos restantes, invalidando el resto del argumento. Una orden de eliminación válida es un ejemplo elemental de shelling). En este punto el triángulo solitario tiene V = 3, E = 3, y F = 1, de modo que V - E + F = 1. Puesto que cada uno de los dos pasos de transformación anteriores conserva esta cantidad, hemos demostrado V - E + F = 1 para el objeto deformado, plano demostrando así V - E + F = 2 para el poliedro. Esto demuestra el teorema. Para pruebas adicionales, véase Veintiuna Pruebas de la Fórmula de Euler por David Eppstein.[2] Múltiples pruebas, incluyendo sus defectos y limitaciones, se utilizan como ejemplos en Pruebas y Refutaciones de Imre Lakatos.[3] Definición topológicaLas superficies poliédricas de las que se ha hablado anteriormente son, en lenguaje moderno, complejos CW finitos bidimensionales. (Cuando sólo se utilizan caras triangulares, son complejos simplicialeses finitos bidimensionales). En general, para cualquier complejo CW finito, la característica de Euler' puede definirse como la suma alternada donde kn denota el número de celdas de dimensión n en el complejo. Análogamente, para un complejo simplicial, la característica de Euler es igual a la suma alterna donde kn denota el número de n-simplexes en el complejo. Alternativa al número de BettiDe forma más general, para cualquier espacio topológico, podemos definir el n número de Betti bn como el rango de homología singular del grupo n. La característica de Euler puede definirse entonces como la suma alternada Esta cantidad está bien definida si los números de Betti son todos finitos y si son cero a partir de un cierto índice n0. Para complejos simpliciales, esta no es la misma definición que en el párrafo anterior, pero un cálculo de homología muestra que las dos definiciones darán el mismo valor para . Generalización a las superficies Una superficie compacta como la esfera, el toro, el bi-toro, un disco con borde, etc. surgen de deformar de forma continua un poliedro. Por ejemplo, si deformamos un icosaedro hasta obtener una esfera las aristas se transformarán en curvas sobre la esfera, las caras serán "triángulos" y los vértices serán puntos sobre las mismas. Así la esfera quedará "triangulada" (Véase triangulación). Para definir la característica de una superficie se usaran estas triangulaciones realizando la fórmula análoga χ(S) = Triángulos - Lados + Vértices. En realidad las triangulaciones no deben ser hechas necesariamente con triángulos, sino con cualquier polígono, teniendo en cuenta que dos polígonos solo compartan una arista como máximo, y que, si comparten un lado, solo compartan los dos vértices de ese lado. Así la generalización de la característica de Euler para una superficie cerrada S es La característica de Euler de superficies orientadas cerradas se relaciona con su género g, que es un número que describe la cantidad de «asas» que tiene la superficie. La relación es dada por: Por ejemplo: El toro (la rosquilla) tiene una asa y por lo tanto . Definición general y propiedadesPara un CW-complejo finito y en particular para un complejo simplicial finito, la característica de Euler se puede definir como la suma alternada donde ki denota el número de células de dimensión i. Entonces, se puede definir la característica de Euler de una variedad como la característica de Euler de un complejo simplicial homeomorfo a él. Por ejemplo, el círculo y el toro tienen característica de Euler 0 y las bolas sólidas tienen característica de Euler 1.
Para las variedades cerradas, la característica de Euler coincide con el número de Euler, es decir, la clase de Euler de su fibrado tangente evaluado en la clase fundamental de la variedad. Para las variedades de Riemann cerradas, la característica de Euler puede encontrarse también integrando la curvatura -- vea el teorema de Gauss-Bonnet para el caso de dos dimensiones y el teorema de Gauss-Bonnet generalizado para el caso general. Un análogo discreto del teorema de Gauss-Bonnet es el teorema de Descartes que el "defecto total" de un poliedro, medido en círculos completos, es la característica de Euler del poliedro; véase defecto (geometría). Más generalmente aún, para cualquier espacio topológico, podemos definir el n-ésimo número de Betti bn como el rango del n-ésimo grupo de homología. La característica de Euler se puede entonces definir como la suma alternada Esta definición tiene sentido si los números de Betti son todos finitos y cero más allá de cierto índice n0. Dos espacios topológicos que son equivalentes homotópicos tienen grupos isomorfos de homología y por lo tanto la misma característica de Euler. De esta definición y la dualidad de Poincaré, se sigue que la característica de Euler de cualquier variedad cerrada de dimensión impar es cero. Si M y N son espacios topológicos, entonces la característica de Euler de su producto M × N es
La característica de Euler se comporta bien con respecto a muchas operaciones básicas sobre espacios topológicos, como sigue. Invariancia de homotopíaLa homología es un invariante topológico, y además un invariante de homotopía: Dos espacios topológicos que son homotópicamente equivalentes tienen isomorfismo de grupos homológicos. De ello se deduce que la característica de Euler es también una invariante homotópica. Por ejemplo, cualquier espacio contráctil (es decir, una homotopía equivalente a un punto) tiene homología trivial, lo que significa que el 0 º número de Betti es 1 y los demás 0. Por lo tanto, su característica de Euler es 1. Por tanto, su característica de Euler es 1. Este caso incluye el espacio euclídeo de cualquier dimensión, así como la bola unitaria sólida en cualquier espacio euclídeo — el intervalo unidimensional, el disco bidimensional, la bola tridimensional, etc. Por poner otro ejemplo, cualquier poliedro convexo es homeomorfo a la bola tridimensional, por lo que su superficie es homeomorfa (por tanto homotópicamente equivalente) a la esfera bidimensional, que tiene característica de Euler 2. Esto explica por qué los poliedros convexos tienen característica de Euler 2. Principio de inclusión-exclusiónSi M y N son dos espacios topológicos cualesquiera, entonces la característica de Euler de su unión disjunta es la suma de sus características de Euler, ya que la homología es aditiva bajo unión disjunta: Más generalmente, si M y N son subespacios de un espacio mayor X, entonces también lo son su unión e intersección. En algunos casos, la característica de Euler obedece a una versión del principio de inclusión-exclusión: Conjunto parcialmente ordenadoEl concepto de característica de Euler de un poset finito acotado es otra generalización, importante en combinatoria. Un poset es acotado si tiene elementos mínimos y máximos, que podemos llamar 0 y 1. La característica de Euler de tal poset es μ(0,1), donde μ es la función de Möbius en el álgebra de incidencia de ese poset. Véase tambiénReferencias
Bibliografía
Enlaces externos
|
Portal di Ensiklopedia Dunia

























