Quiver (mathematics)
|
Read other articles:

Divizia A 1978-1979 Competizione Liga I Sport Calcio Edizione 61ª Organizzatore FRF Date dal 24 agosto 1978al 24 giugno 1979 Luogo Romania Partecipanti 18 Risultati Vincitore Argeș Pitești(2º titolo) Retrocessioni Bihor OradeaCorvinul HunedoaraUTA Arad Statistiche Miglior marcatore Marin Radu (22) Cronologia della competizione 1977-1978 1979-1980 Manuale La Divizia A 1978-1979 è stata la 61ª edizione della massima serie del campionato di calcio rumeno, disputato tra il 2…
Världsmästerskapet i ishockey för herrar 1937Datum17–27 februari 1937DeltagareNationer ihuvudmästerskap11VärdskapLand StorbritannienSpelplatserLondonPlaceringar Guld Kanada Silver Storbritannien Brons SchweizÖvrigtMatcher37Mål214 (5,78 mål per match)← 1936 Tyskland Tjeckoslovakien 1938 → Världsmästerskapet i ishockey 1937 var det elfte världsmästerskapet i ishockey, arrangerat av IIHF, och matcherna europeiska lag emellan gällde samtidigt som d…

贝内德托·贝蒂诺·克拉克西Bettino Craxi第45任意大利总理任期1983年8月4日—1987年4月17日总统亚历山德罗·佩尔蒂尼 弗朗切斯科·科西加副职阿纳尔多·福拉尼前任阿明托雷·范范尼继任阿明托雷·范范尼 个人资料出生(1934-02-24)1934年2月24日伦巴第米兰逝世2000年1月19日(2000歲—01—19)(65歲)突尼斯哈马麦特国籍意大利政党意大利社会党儿女Bobo、Stefania 克拉克西在突尼斯的墓地。 贝�…

Torre Einstein a Potsdam vicino a Berlino, 1919-1922 (Erich Mendelsohn). Goetheanum a Dornach vicino a Basilea in Svizzera, 1924-1928 (Rudolf Steiner). Espressionismo olandese (scuola di Amsterdam), condominio Het Schip ad Amsterdam, 1917-20 (Michel de Klerk). L'architettura espressionista è stata un movimento architettonico attivo in Europa durante i primi decenni del XX secolo, strettamente connesso alla nascita ed allo sviluppo dell'arte espressionista nel settore delle arti visive e del…
2020年夏季奥林匹克运动会波兰代表團波兰国旗IOC編碼POLNOC波蘭奧林匹克委員會網站olimpijski.pl(英文)(波兰文)2020年夏季奥林匹克运动会(東京)2021年7月23日至8月8日(受2019冠状病毒病疫情影响推迟,但仍保留原定名称)運動員206參賽項目24个大项旗手开幕式:帕维尔·科热尼奥夫斯基(游泳)和马娅·沃什乔夫斯卡(自行车)[1]闭幕式:卡罗利娜·纳亚(皮划艇)[2…
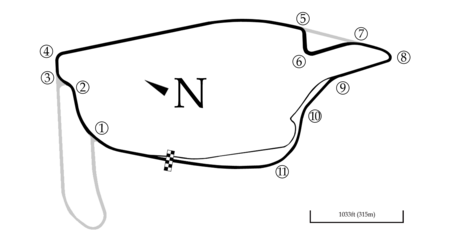
Motor race meeting 2015 ITM 500 AucklandEvent InformationRound 12 of 14 in the 2015 International V8 Supercars ChampionshipDate6–8 November 2015LocationPukekohe, New ZealandVenuePukekohe Park RacewayWeatherFineResultsRace 1Distance 21 laps 60 kmPole position Jamie WhincupTriple Eight Race Engineering 1:03.3203Winner Jamie WhincupTriple Eight Race Engineering 24:48.8376Race 2Distance 21 laps 60 kmPole position David ReynoldsRod Nash Racing 1:02.4690Winner David ReynoldsRod Nash Racing 26:37.956…

هذه المقالة بحاجة لصندوق معلومات. فضلًا ساعد في تحسين هذه المقالة بإضافة صندوق معلومات مخصص إليها. هذه المقالة يتيمة إذ تصل إليها مقالات أخرى قليلة جدًا. فضلًا، ساعد بإضافة وصلة إليها في مقالات متعلقة بها. (أبريل 2020) هذه المقالة هي جزء من سلسلةتاريخ اليونان العصر الحجري الحدي…

Sage writing was a genre of creative nonfiction popular in the Victorian era. The concept originates with John Holloway's 1953 book The Victorian Sage: Studies in Argument. Sage writing is a development from ancient wisdom literature in which the writer chastises and instructs the reader about contemporary social issues, often utilising discourses of philosophy, history, politics, and economics in non-technical ways. Prominent examples of the genre include writings by Thomas Carlyle, Matthew Arn…

Artikel ini tidak memiliki referensi atau sumber tepercaya sehingga isinya tidak bisa dipastikan. Tolong bantu perbaiki artikel ini dengan menambahkan referensi yang layak. Tulisan tanpa sumber dapat dipertanyakan dan dihapus sewaktu-waktu.Cari sumber: 12 Giant Hits – berita · surat kabar · buku · cendekiawan · JSTOR 12 Giant HitsAlbum kompilasi karya Johnny CashDirilis1990GenreCountryLabelCBS 12 Giant Hits adalah album kompilasi yang dirilis oleh CBS…

Protected area in Queensland, AustraliaBellthorpe National ParkQueenslandIUCN category II (national park) The range in the background is in the national park.Bellthorpe National ParkNearest town or cityWoodfordCoordinates26°51′57″S 152°41′21″E / 26.86583°S 152.68917°E / -26.86583; 152.68917Area75.5 km2 (29.2 sq mi)Managing authoritiesQueensland Parks and Wildlife ServiceWebsiteBellthorpe National ParkSee alsoProtected areas of Queensland Belltho…

Cycling at the Olympics Cyclingat the Games of the VII OlympiadVenuesAntwerp and surrounding areaVélodrome d'Anvers ZuremborgDate9 –13 August 1920Competitors103 from 14 nations← 19121924 → The cycling competitions at the 1920 Summer Olympics in Antwerp consisted of two road racing events and four track racing events, all for men only.[1] The 50 km track event was held for the first time at these Games. Medal summary Road cycling Games Gold Sil…

British Conservative politician (1918–1994) For the football player, see Keith Joseph (American football). For the Australian bishop, see Keith Joseph (bishop). The Right HonourableThe Lord JosephCH PCJoseph in 1964Secretary of State for Education and ScienceIn office11 September 1981 – 21 May 1986Prime MinisterMargaret ThatcherPreceded byMark CarlisleSucceeded byKenneth BakerSecretary of State for IndustryIn office4 May 1979 – 11 September 1981Prime MinisterMargaret …

Political convention of the Republican Party This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: 1980 Republican National Convention – news · newspapers · books · scholar · JSTOR (January 2009) (Learn how and when to remove this message) 1980 Republican National Convention1980 presidential election NomineesReagan a…

American politician (1914–1983) For other people named William E. Miller, see William E. Miller (disambiguation). William E. MillerMiller c. 196444th Chair of the Republican National CommitteeIn officeJune 2, 1961 – June 15, 1964Preceded byThruston MortonSucceeded byDean Burch11th Chair of the National Republican Congressional CommitteeIn office1960–1961Preceded byRichard M. SimpsonSucceeded byBob WilsonMember of theU.S. House of Representativesfrom New YorkIn officeJanuary …

British TV series or programme WorklifeWorklife titlesAlso known asBusiness Edition withTanya Beckett(2010–2015)Business Edition withJamie Robertson(2011–2014)Business Live(2015–2019)Created byBBC World NewsBBC News ChannelPresented bySally BundockBen ThompsonCountry of originUnited KingdomOriginal languageEnglishProductionProduction locationsStudio C, Broadcasting House, London / Singapore / New York CityRunning time30 minutesOriginal releaseNetworkBBC World NewsBBC News ChannelRelease1&#…

2005 film score by Patrick DoyleHarry Potter and the Goblet of Fire (Original Motion Picture Soundtrack)Film score by Patrick DoyleReleased15 November 2005 (2005-11-15)Recorded2005StudioAir Lyndhurst StudiosGenreSoundtrackLength75:58Patrick Doyle chronology Nanny McPhee(2005) Harry Potter and the Goblet of Fire (Original Motion Picture Soundtrack)(2005) Jekyll & Hyde(2006) Wizarding World soundtrack chronology Harry Potter and the Prisoner of Azkaban (Original Motion P…

Japanese literary award for children's literature This article has multiple issues. Please help improve it or discuss these issues on the talk page. (Learn how and when to remove these template messages) The topic of this article may not meet Wikipedia's general notability guideline. Please help to demonstrate the notability of the topic by citing reliable secondary sources that are independent of the topic and provide significant coverage of it beyond a mere trivial mention. If notability canno…

Southwestern area of England For the region in Norway translated as West Country, see Vestlandet. Place in EnglandWest CountryOne interpretation of the West Country, shown on this map as identical to the South West region of England, incorporating the counties of Bristol, Cornwall, Devon, Dorset, Gloucestershire, Somerset, and WiltshireCountryUnited Kingdom The West Country (Cornish: An Tir West) is a loosely defined area within southwest England,[1] usually taken to include the counties…
Main article: Football at the 2023 Pacific Games 2023 Pacific Gameswomen's football tournamentTournament detailsHost countrySolomon IslandsCityHoniaraDates17 November–2 DecemberTeams10 (from 1 confederation)Venue(s)2 (in 1 host city)Final positionsChampions Papua New Guinea (6th title)Runners-up FijiThird place New CaledoniaFourth place SamoaTournament statisticsMatches played20Goals scored82 (4.1 per match)Top scorer(s) Ramona Padio(11 goals)← 201…

American sign company This article may contain excessive or inappropriate references to self-published sources. Please help improve it by removing references to unreliable sources where they are used inappropriately. (February 2023) (Learn how and when to remove this message) Daktronics, Inc.Company typePublicTraded asNasdaq: DAKTIndustryElectronicsFounded1968; 56 years ago (1968)[1]FounderAelred J. KurtenbachDuane SanderHeadquartersBrookings, South Dakota, United …















![{\displaystyle E\;{\begin{matrix}s\\[-6pt]\rightrightarrows \\[-4pt]t\end{matrix}}\;V}](https://wikimedia.org/api/rest_v1/media/math/render/svg/53c706fee42f1490f68d670d43eacd709f3af816)


















