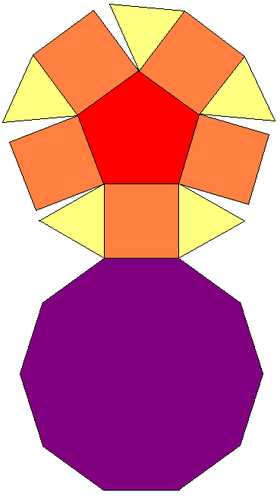
5th Johnson solid (12 faces)
Properties
The pentagonal cupola 's faces are five equilateral triangles , five squares , one regular pentagon , and one regular decagon .[ 1] convexity and regular polygonal faces, from which it is classified as the fifth Johnson solid .[ 2] elementary polyhedron 's example.[ 3]
The following formulae for circumradius
R
{\displaystyle R}
h
{\displaystyle h}
surface area
A
{\displaystyle A}
volume
V
{\displaystyle V}
faces are regular with edge length
a
{\displaystyle a}
[ 4]
h
=
5
−
5
10
a
≈
0.526
a
,
R
=
11
+
4
5
2
a
≈
2.233
a
,
A
=
20
+
5
3
+
5
(
145
+
62
5
)
4
a
2
≈
16.580
a
2
,
V
=
5
+
4
5
6
a
3
≈
2.324
a
3
.
{\displaystyle {\begin{aligned}h&={\sqrt {\frac {5-{\sqrt {5}}}{10}}}a&\approx 0.526a,\\R&={\frac {\sqrt {11+4{\sqrt {5}}}}{2}}a&\approx 2.233a,\\A&={\frac {20+5{\sqrt {3}}+{\sqrt {5\left(145+62{\sqrt {5}}\right)}}}{4}}a^{2}&\approx 16.580a^{2},\\V&={\frac {5+4{\sqrt {5}}}{6}}a^{3}&\approx 2.324a^{3}.\end{aligned}}}
It has an axis of symmetry passing through the center of both top and base, which is symmetrical by rotating around it at one-, two-, three-, and four-fifth of a full-turn angle. It is also mirror-symmetric relative to any perpendicular plane passing through a bisector of the hexagonal base. Therefore, it has pyramidal symmetry , the cyclic group
C
5
v
{\displaystyle C_{5\mathrm {v} }}
[ 3]
The pentagonal cupola can be applied to construct a polyhedron . A construction that involves the attachment of its base to another polyhedron is known as augmentation ; attaching it to prisms or antiprisms is known as elongation or gyroelongation .[ 5] [ 6] elongated pentagonal cupola
J
20
{\displaystyle J_{20}}
gyroelongated pentagonal cupola
J
24
{\displaystyle J_{24}}
pentagonal orthobicupola
J
30
{\displaystyle J_{30}}
pentagonal gyrobicupola
J
31
{\displaystyle J_{31}}
pentagonal orthocupolarotunda
J
32
{\displaystyle J_{32}}
pentagonal gyrocupolarotunda
J
33
{\displaystyle J_{33}}
elongated pentagonal orthobicupola
J
38
{\displaystyle J_{38}}
elongated pentagonal gyrobicupola
J
39
{\displaystyle J_{39}}
elongated pentagonal orthocupolarotunda
J
40
{\displaystyle J_{40}}
gyroelongated pentagonal bicupola
J
46
{\displaystyle J_{46}}
gyroelongated pentagonal cupolarotunda
J
47
{\displaystyle J_{47}}
augmented truncated dodecahedron
J
68
{\displaystyle J_{68}}
parabiaugmented truncated dodecahedron
J
69
{\displaystyle J_{69}}
metabiaugmented truncated dodecahedron
J
70
{\displaystyle J_{70}}
triaugmented truncated dodecahedron
J
71
{\displaystyle J_{71}}
gyrate rhombicosidodecahedron
J
72
{\displaystyle J_{72}}
parabigyrate rhombicosidodecahedron
J
73
{\displaystyle J_{73}}
metabigyrate rhombicosidodecahedron
J
74
{\displaystyle J_{74}}
trigyrate rhombicosidodecahedron
J
75
{\displaystyle J_{75}}
diminishment : diminished rhombicosidodecahedron
J
76
{\displaystyle J_{76}}
paragyrate diminished rhombicosidodecahedron
J
77
{\displaystyle J_{77}}
metagyrate diminished rhombicosidodecahedron
J
78
{\displaystyle J_{78}}
bigyrate diminished rhombicosidodecahedron
J
79
{\displaystyle J_{79}}
parabidiminished rhombicosidodecahedron
J
80
{\displaystyle J_{80}}
metabidiminished rhombicosidodecahedron
J
81
{\displaystyle J_{81}}
gyrate bidiminished rhombicosidodecahedron
J
82
{\displaystyle J_{82}}
tridiminished rhombicosidodecahedron
J
83
{\displaystyle J_{83}}
[ 1]
References
^ a b Berman, Martin (1971). "Regular-faced convex polyhedra". Journal of the Franklin Institute . 291 (5): 329– 352. doi :10.1016/0016-0032(71)90071-8 . MR 0290245 . ^ Uehara, Ryuhei (2020). Introduction to Computational Origami: The World of New Computational Geometry doi :10.1007/978-981-15-4470-5 . ISBN 978-981-15-4470-5 S2CID 220150682 . ^ a b Johnson, Norman W. (1966). "Convex polyhedra with regular faces" . Canadian Journal of Mathematics 18 : 169– 200. doi :10.4153/cjm-1966-021-8 MR 0185507 . S2CID 122006114 . Zbl 0132.14603 .^ Braileanu1, Patricia I.; Cananaul, Sorin; Pasci, Nicoleta E. (2022). "Geometric pattern infill influence on pentagonal cupola mechanical behavior subject to static external loads" . Journal of Research and Innovation for Sustainable Society . 4 (2). Thoth Publishing House: 5– 15. doi :10.33727/JRISS.2022.2.1:5-15 ISSN 2668-0416 . {{cite journal }}: CS1 maint: DOI inactive as of December 2024 (link ) CS1 maint: numeric names: authors list (link )^ Demey, Lorenz; Smessaert, Hans (2017). "Logical and Geometrical Distance in Polyhedral Aristotelian Diagrams in Knowledge Representation" . Symmetry . 9 (10): 204. Bibcode :2017Symm....9..204D . doi :10.3390/sym9100204 ^ Slobodan, Mišić; Obradović, Marija; Ðukanović, Gordana (2015). "Composite Concave Cupolae as Geometric and Architectural Forms" (PDF) . Journal for Geometry and Graphics . 19 (1): 79– 91.
External links